Quel est le programme C/C++ pour le nième nombre catalan ?

Les nombres catalans sont une série de nombres. Les nombres catalans sont une séquence de nombres naturels qui apparaissent dans divers problèmes de comptage, impliquant souvent des objets définis de manière récursive.

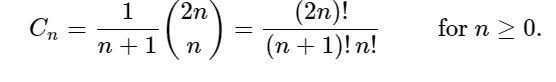
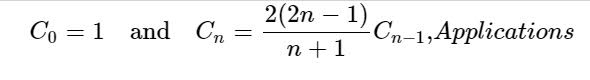
• C_n est le nombre de mots Dyck de longueur 2n. Un mot Dyck est une chaîne composée de n X et de n Y tels que le nombre de Y ne dépasse pas le nombre de X dans tout fragment initial de la chaîne. Par exemple, voici un mot de Dyck de longueur 6 :

XXXYYY XYXXYY XYXYXY XXYYXY XXYXYY.

• réinterprète le symbole La quantité

  ((())) ()(()) ()()() (())() (()())

  Copier après la connexion

C
• n

  est le nombre de façons différentes dont n + 1 facteurs peuvent être complètement clos (ou le nombre de façons dont n applications d'opérateurs binaires associés). Par exemple, pour n = 3, nous avons cinq parenthèses différentes pour les quatre facteurs suivants :

  ((ab)c)d (a(bc))d (ab)(cd) a((bc)d) a(b(cd))

  Copier après la connexion

Les applications consécutives d'opérateurs binaires peuvent être représentées par un arbre binaire complet. (Un arbre binaire enraciné est dit complet si chaque sommet a soit deux nœuds enfants, soit aucun nœud enfant.) À partir de là, C
• n

  est le nombre d'arbres binaires complets avec n + 1 feuilles :

Exemple

- 6

- 1 1 2 5 14 42Explication

Quand n = 0, 1, 2, 3,4,5,6,7,8,9,10, .. ., les n premiers nombres catalans sont

1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862,

Exemple

#include<iostream>
using namespace std;
long int catalan( int n) {
   if (n <= 1){
      return 1;
   }
   long int result = 0;
   for (int i=0; i<n; i++){
      result += catalan(i)*catalan(n-i-1);
   }
   return result;
}
int main(){
   for (int i=0; i<6; i++)
   cout << catalan(i) << " ";
   return 0;
}

Sortie

1 1 2 5 14 42

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!