Programme C pour souris dans le labyrinthe - backtracking-2

Le rat dans le labyrinthe est également un problème courant lié au retour en arrière. I

Un labyrinthe est une matrice bidimensionnelle dans laquelle certaines cellules sont bloquées. L’une des cellules est la cellule source et nous devons partir de là. Un autre élément est la destination, l’endroit où nous devons arriver. Nous devons trouver un chemin de la source à la destination sans entrer dans aucune cellule bloquée. Une image du labyrinthe non résolu est présentée ci-dessous.

C'est la solution pour cela.

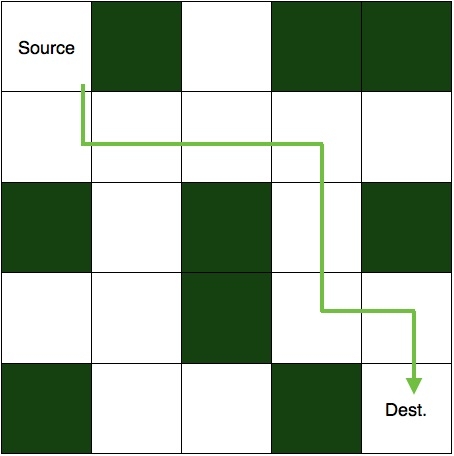
Pour résoudre cette énigme, nous partons d'abord de l'unité source et nous nous dirigeons dans la direction où le chemin n'est pas bloqué. Si le chemin emprunté nous mène à notre destination, l’énigme est résolue. Sinon, nous reviendrons et changerons la direction du chemin sur lequel nous nous trouvons. Nous implémenterons également la même logique dans le code.

Input:
maze[][] = {
{0,1,0,1,1},
{0,0,0,0,0},
{1,0,1,0,1},
{0,0,1,0,0},
{1,0,0,1,0}}

Output:
1 0 0 0 0
1 1 1 1 0
0 0 0 1 0
0 0 0 1 1
0 0 0 0 1

Explication

Tout d'abord, nous allons créer une matrice pour représenter le labyrinthe, les éléments de la matrice seront 0 ou 1. 1 signifie cellules bloquées et 0 signifie cellules que nous pouvons déplacer. La matrice du labyrinthe ci-dessus est la suivante :

0 1 0 1 1
0 0 0 0 0
1 0 1 0 1
0 0 1 0 0
1 0 0 1 0

Maintenant, nous allons créer une autre matrice des mêmes dimensions pour stocker la solution. Ses éléments seront également 0 ou 1. 1 représentera les cellules sur notre chemin et les cellules restantes seront 0. La matrice représentant la solution est :

1 0 0 0 0
1 1 1 1 0
0 0 0 1 0
0 0 0 1 1
0 0 0 0 1

Nous avons donc maintenant notre matrice. Ensuite, nous trouverons le chemin de la cellule de départ à la cellule cible, les étapes que nous suivrons sont les suivantes :

• Vérifiez la cellule actuelle, si c'est la cellule cible, le puzzle est résolu.

• Sinon, essayez de descendre et voyez si vous pouvez passer à la cellule suivante (pour passer à une cellule, elle doit être vide et non dans le chemin).

• Si vous pouvez passer à la cellule suivante, continuez à avancer le long du chemin jusqu'à la cellule inférieure suivante.

• Sinon, essayez de vous déplacer vers la droite. Si le côté droit est bloqué ou occupé, montez.

• De même, si remonter n'est pas possible, nous nous déplacerons simplement vers la cellule de gauche.

• Si le mouvement n'est possible dans aucune des quatre directions (bas, droite, haut ou gauche), revenez simplement en arrière et modifiez le chemin actuel (retour en arrière).

Donc, pour résumer, on essaie de se déplacer de la cellule actuelle vers d'autres cellules (bas, droite, haut et gauche) et si aucun mouvement n'est possible, revenir en arrière et changer la direction du chemin vers une autre grille cellulaire.

printsolution → Cette fonction imprime simplement la matrice de solution.

solvemaze → C'est la fonction qui implémente réellement l'algorithme de backtracking. Tout d'abord, nous vérifions si notre cellule est la cellule cible, si c'est le cas (r==SIZE-1) et (c==SIZE-1). Si c'est la cellule cible, notre énigme est résolue. Sinon, nous vérifions s'il s'agit d'un mobile valide. Une cellule valide doit être dans la matrice, c'est-à-dire que l'index doit être compris entre 0 et SIZE-1, r>=0 && c>=0 && r

Exemple

#include <iostream>
using namespace std;
#define SIZE 5
//the maze problem
int maze[SIZE][SIZE] = {
   {0,1,0,1,1},
   {0,0,0,0,0},
   {1,0,1,0,1},
   {0,0,1,0,0},
   {1,0,0,1,0}
};
//matrix to store the solution
int solution[SIZE][SIZE];
//function to print the solution matrix
void printsolution() {
   int i,j;
   for(i=0;i<SIZE;i++) {
      for(j=0;j<SIZE;j++) {
         printf("%d\t",solution[i][j]);
      }
      printf("</p><p></p><p>");
   }
}
//function to solve the maze
//using backtracking
int solvemaze(int r, int c) {
   //if destination is reached, maze is solved
   //destination is the last cell(maze[SIZE-1][SIZE-1])
   if((r==SIZE-1) && (c==SIZE-1) {
      solution[r][c] = 1;
      return 1;
   }
   //checking if we can visit in this cell or not
   //the indices of the cell must be in (0,SIZE-1)
   //and solution[r][c] == 0 is making sure that the cell is not already visited
   //maze[r][c] == 0 is making sure that the cell is not blocked
   if(r>=0 && c>=0 && r<SIZE && c<SIZE && solution[r][c] == 0 && maze[r][c] == 0){
      //if safe to visit then visit the cell
      solution[r][c] = 1;
      //going down
      if(solvemaze(r+1, c))
         return 1;
      //going right
      if(solvemaze(r, c+1))
         return 1;
      //going up
      if(solvemaze(r-1, c))
         return 1;
      //going left
      if(solvemaze(r, c-1))
         return 1;
      //backtracking
      solution[r][c] = 0;
      return 0;
   }
   return 0;
}
int main() {
   //making all elements of the solution matrix 0
   int i,j;
   for(i=0; i<SIZE; i++) {
      for(j=0; j<SIZE; j++) {
         solution[i][j] = 0;
      }
   }
   if (solvemaze(0,0))
      printsolution();
   else
      printf("No solution</p><p>");
   return 0;
}

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!