Si pas plus de deux points du plan sont colinéaires, quel est le nombre de triangles ?

Voyons comment compter le nombre de triangles sur un plan étant donné n points et limiter le nombre de points colinéaires à deux maximum.

Le calcul du nombre de triangles dans un plan ne comportant pas plus de deux points colinéaires est un problème typique de la géométrie computationnelle, qui est appliqué à l'infographie, au traitement d'images et à d'autres domaines de l'informatique.

Par exemple, lors de la création d'une image 2D à partir d'une scène 3D dans des graphiques 3D, le problème peut survenir du calcul de triangles dans un plan ne comportant pas plus de deux points colinéaires. Dans ce cas, le processus de comptage de triangles peut être utilisé pour déterminer combien de triangles sont présents dans l’image 2D finale après projection de la scène 3D sur un plan. Cela vous permet de déterminer la complexité de la scène et d'augmenter la vitesse de rendu.

En traitement d'image, nous pouvons vouloir compter le nombre d'objets ou de formes uniques dans une image, cette question est utile. Dans ce cas, nous pouvons représenter l’image comme une collection de points sur un plan, puis compter le nombre de triangles qui peuvent être créés entre ces points en appliquant des techniques de comptage de triangles. Nous pouvons déterminer le nombre approximatif d’éléments ou de formes différents dans une image en comptant le nombre de triangles formés.

Instructions

Comprenons ce problème à travers quelques exemples et essayons de le résoudre. ​​

Le but est de déterminer combien de triangles sont formés sur un plan avec n points tels que pas plus de deux points soient colinéaires.

Exemple -

Supposons que N soit le nombre de points sur l'avion.

N = 3

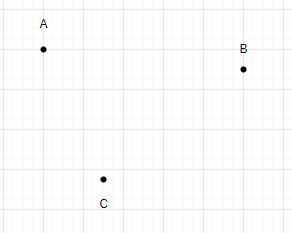
En utilisant ces points, nous ne pouvons dessiner qu'un triangle.

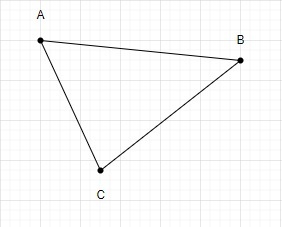
Le nombre total de triangles formés à partir de 3 points est donc 1.

Soit N = 4

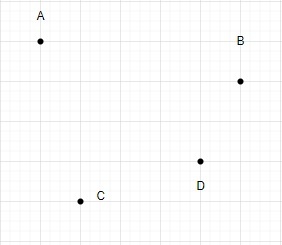
Traçons un triangle en utilisant ces quatre points.

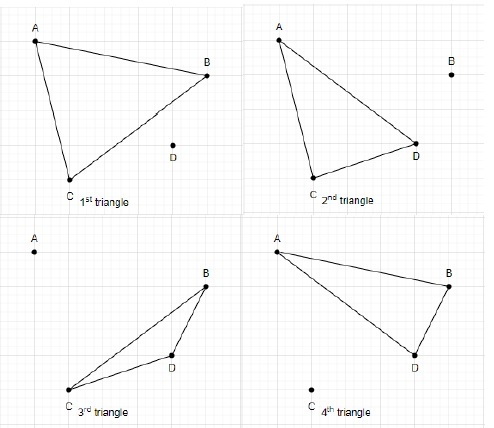
Le nombre total de triangles formés à l'aide de 4 points est de 4.

Regardons quelques-uns des calculs impliqués dans le calcul du nombre de triangles. Ceci peut être obtenu en utilisant des permutations et des combinaisons. Pour construire un triangle, vous avez besoin de 3 points sur le total à la fois.

Ainsi, si un plan contient n points et que pas plus de deux d'entre eux sont colinéaires, alors le nombre de triangles dans le plan est donné par la formule suivante.

$$mathrm{n_{C_{3}}:=:frac{n(n-1):(n-2)}{6}}$$

Méthode

Le programme trouve le nombre de triangles dans le plan si pas plus de deux points sont colinéaires, en utilisant l'algorithme suivant.

• Prenez le nombre de points sur le plan en entrée et limitez-le à pas plus de deux points colinéaires.

• Calculez le nombre total de triangles en utilisant la formule ci-dessus.

• Imprimez le nombre total de triangles en sortie.

Exemple

Programme C++ pour calculer le nombre de triangles dans un plan si pas plus de deux points sont colinéaires.

#include <iostream>
using namespace std;

int main() {
   int number_of_points = 4;
   int number_of_triangle;
   
   number_of_triangle = number_of_points * (number_of_points - 1) * (number_of_points - 2) / 6;
   cout << "Total number of triangles formed using " << number_of_points<< " points = " <<  number_of_triangle << endl;
   
   return 0;
}

Sortie

Total number of triangles formed using 4 points = 4

Complexité

Complexité temporelle : O(1) puisque ce code effectue un nombre fixe de calculs quelle que soit la taille d'entrée.

Complexité spatiale : O(1) car le code utilise un nombre fixe de variables pour stocker les valeurs d'entrée et les résultats quelle que soit la taille de l'entrée.

Conclusion

Dans cet article, nous essayons d'expliquer la méthode pour trouver le nombre total de triangles possibles avec n points donnés, avec la contrainte qu'il n'y a pas deux points colinéaires. J'espère que cet article vous aidera à mieux apprendre ce concept.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!