How to find the definite integral of a function on the geometric sketchpad

php Editor Baicao reveals to you Winter Rhapsody, a character plot simulation game with a small town story as the background. Integrating Japanese characteristic elements, the game has a wealth of puzzle challenges and skill-based gameplay, and operating skills are crucial. Players can unlock various skills for a more comprehensive gaming experience. Wonderful special content is waiting for your experience, let’s explore the charm of winter together!

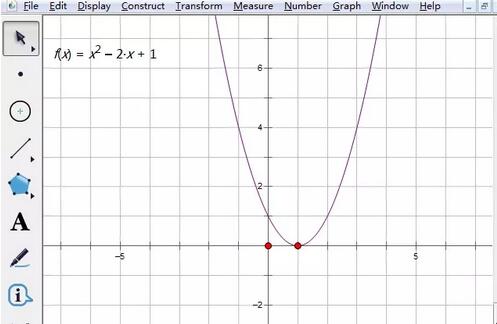
For example, the definite integral of the function f(x)=x2-2x 1 on the interval [-2, 3] is actually the area enclosed by the quadratic function image in the interval and the x-axis. , the specific operation is as follows:

Adjust the [Draw] menu in the menu bar, select the [Draw New Function] command in its drop-down option, enter the function expression in the pop-up function edit box, and click OK. At this time, the function image is clearly visible, and the position of the coordinate system can be moved appropriately with the mouse.

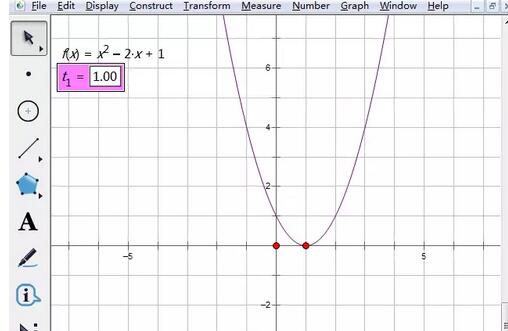
New parameters. To find the definite integral of a function, you need to create a new parameter. Click the [Data] menu in the upper menu bar and select the [New Parameter] command from the drop-down option. In the small window that pops up, enter the parameter value. Just choose the default name and value here. , and then click OK.

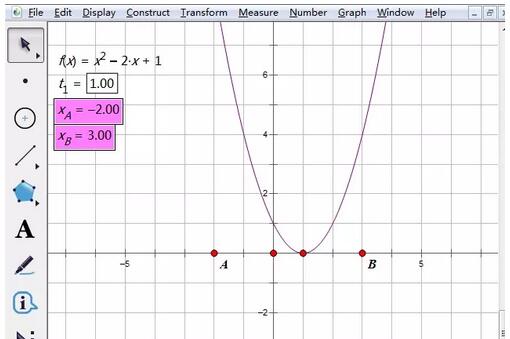
Draw the endpoints of the interval. Without this step, it is inaccurate to just move the mouse to determine the upper and lower limits of the definite integral. If you move around, the upper and lower limits and the abscissa of the endpoint are always not exactly right, which means that the upper and lower limits of the definite integral are inaccurate. Click the [Draw] menu in the upper menu bar, select the [Draw Point] command from its drop-down option, enter the coordinates of the left endpoint of the interval (-2, 0), click Draw, and draw point A. Then, enter the coordinates of the right end point of the interval (3, 0), click Draw, draw point B, and then click Finish to close the small window for drawing the point. Right-click the two endpoints A and B respectively, select the abscissa option, and their abscissas will be displayed on the left.

Set up custom tools. Click the [Custom Tools] button on the left sidebar, and select [Function Tool] from the pop-up tool menu - the definite integral of a function, as shown in the figure below.

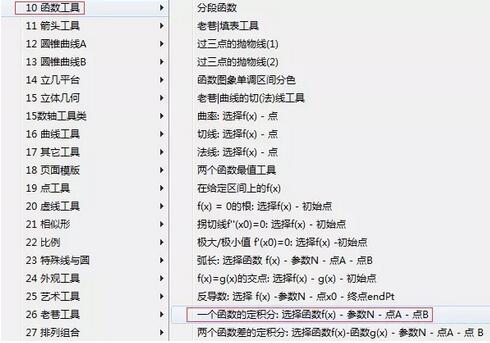
Click function f(x), parameter t1, and pay attention to the order. Then move the mouse and click on point A. When we align, the value on the left representing the lower limit of the definite integral and the abscissa of point A will be the same.

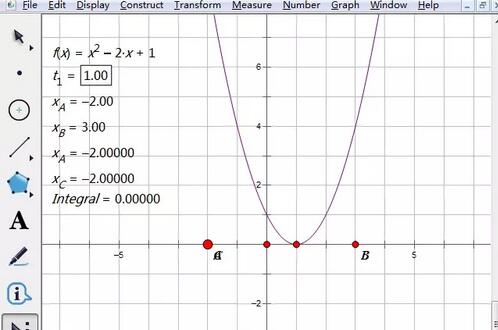
Then move the mouse to point B and click once, release the mouse, and the upper and lower limits of the definite integral and the integral value will be displayed in front of us. Why do we draw the endpoints of the integral interval? It is to align the upper and lower limits and to accurately find the value of the definite integral.

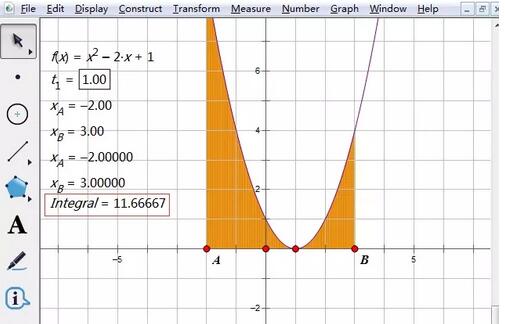
The above is the detailed content of How to find the definite integral of a function on the geometric sketchpad. For more information, please follow other related articles on the PHP Chinese website!