The perfect encounter between PHP and the golden section sequence (not to be missed)

In life, the things we distinguish as beautiful with the naked eye often magically contain the golden ratio. At this time, we have to sigh: the beauty of mathematics is everywhere. The limit of the ratio between the last term and the previous term of the golden section sequence (also known as the Fibonacci sequence) is the root of two-half minus one, which is approximately equal to 0.618 (i.e. the golden section ratio). So how to implement the golden section sequence using PHP? Don’t worry, let’s take our time to understand.

First of all, let’s understand the Golden Section Sequence (i.e. Fibonacci Sequence):

The Fibonacci Sequence refers to this A sequence:

1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765....

That is: the first two values ​​​​are 1. Starting from the third digit, each digit is the sum of the first two digits of the current digit.

The regular formula is:

Fn = F(n-1) F(n 1)

• F: refers to the current sequence

• n: the subscript of the exponential column

Okay , after understanding the golden section sequence (Fibonacci sequence), let’s take a look at how to implement it using PHP.

Method 1: Use arrays

Observe the sequence given above, and combine it with array knowledge to analyze:

• When the array subscript is 0 or 1, the value of the element is 1; when the array subscript is 2, the value of the element is
  a[ 0] a[1]

  ;

• When the array index is 3, the element is a[1] a[2]

  ;

• ....

• When the array subscript is n, the element is

  a[n-2] a[n-1];

• It can be concluded:

a[0]=1

• a[1]=2

• ##a[n]=a[n-2] a[n-1] (n>2)

• ##Code implementation:

  <?php
  header("Content-type:text/html;charset=utf-8");
  function test($num){
      $arr=[];
      for($i=0;$i<$num;$i++)
      {
          if($i==0 || $i==1){
              $arr[$i]=1;
          }else{
              $arr[$i]=$arr[$i-1]+$arr[$i-2];
          }
  		echo $arr[$i]." ";
      }
  }
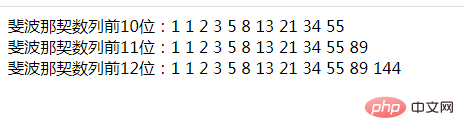
  echo "斐波那契数列前10位：";
  test(10);
  echo "<br>斐波那契数列前11位：";
  test(11);
  echo "<br>斐波那契数列前12位：";
  test(12);
  ?>

  Copy after login
  Output:

Method 2: Use recursion

<?php
header("Content-type:text/html;charset=utf-8");
function fbnq($n) {
	if ($n <= 0) {
		return 0;
	}
	if ($n == 1 || $n == 2) {
		return 1;
	}
	return fbnq($n - 1) + fbnq($n - 2);
}

echo "斐波那契数列第10位：" . fbnq(10);
echo "<br>斐波那契数列第11位：" . fbnq(11);
echo "<br>斐波那契数列第12位：" . fbnq(12);
?>

The recursive method is also implemented ,Is not it simple!

The recursive algorithm can solve a responsible problem using shorter code, but its operation efficiency is relatively low.

php video tutorial

The above is the detailed content of The perfect encounter between PHP and the golden section sequence (not to be missed). For more information, please follow other related articles on the PHP Chinese website!