Breadth-first traversal of a graph is horizontal-first traversal, similar to layer-by-layer traversal of a binary tree. Breadth-first traversal searches and traverses along the width of the tree starting from the root node, that is, traversing in a hierarchical manner; each layer is visited sequentially from top to bottom, and in each layer, from left to right (or right to left) To access nodes, after accessing one level, enter the next level until no nodes can be accessed.
Similar to tree traversal, graph traversal also starts from a certain point in the graph, and then traverses it according to a certain method. All vertices in the graph are visited only once.
But graph traversal is more complicated than trees. Because any vertex in the graph may be adjacent to other vertices, the visited vertices must be recorded during graph traversal to avoid repeated visits.
According to different search paths, we can divide the methods of graph traversal into two types: breadth-first search and depth-first search.
The vertex pair (u, v) is unordered, that is, (u, v ) and (v, u) are the same side. Usually expressed by a pair of parentheses.
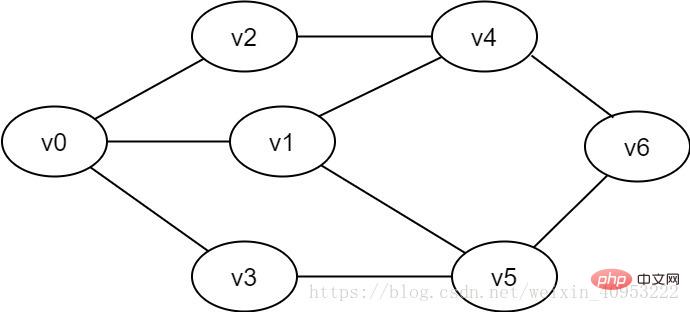
Figure 2-1-1 Example of an undirected graph
The vertex pair
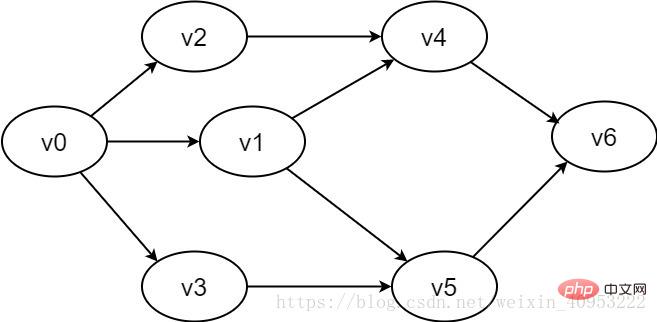
Figure 2-1-2 Example of a directed graph
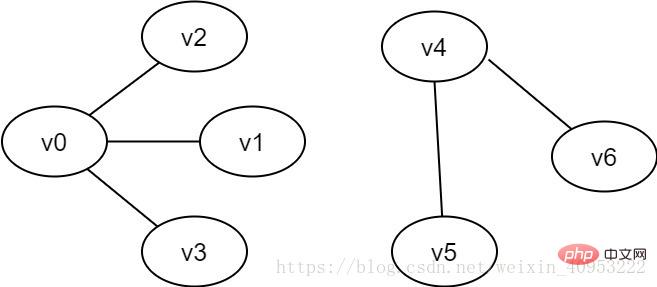
Figure 2-3 Example of a non-connected graph
White means it has not been visited, gray means it is about to be visited, and black means it has been visited.
visited array: 0 means not visited, 1 means visited.
Queue: elements come out from the head of the queue and elements enter from the tail.
1. Initially, all vertices have not been visited, the visited array is initialized to 0, and there are no elements in the queue.
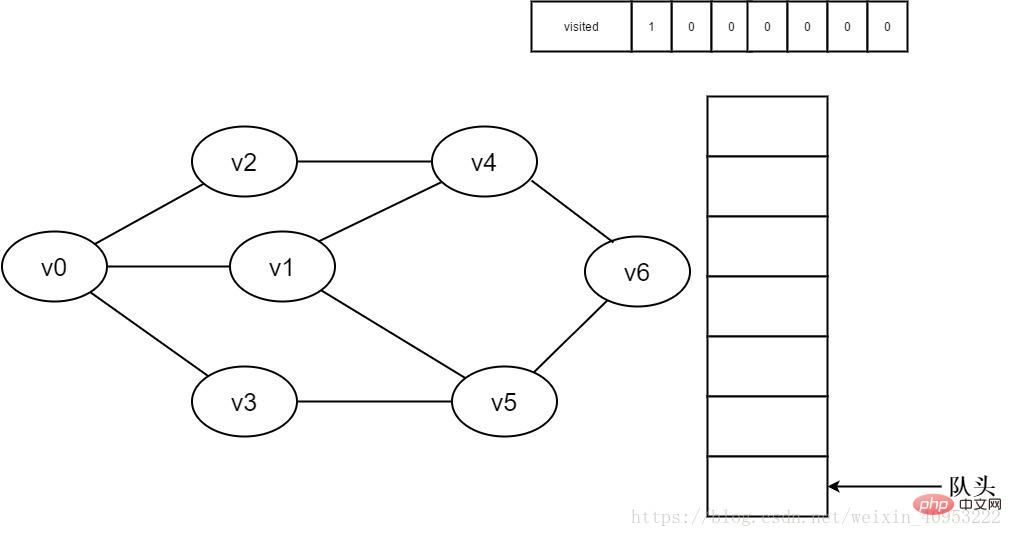
Figure 3-2-1
#2. Vertex v0 is about to be visited.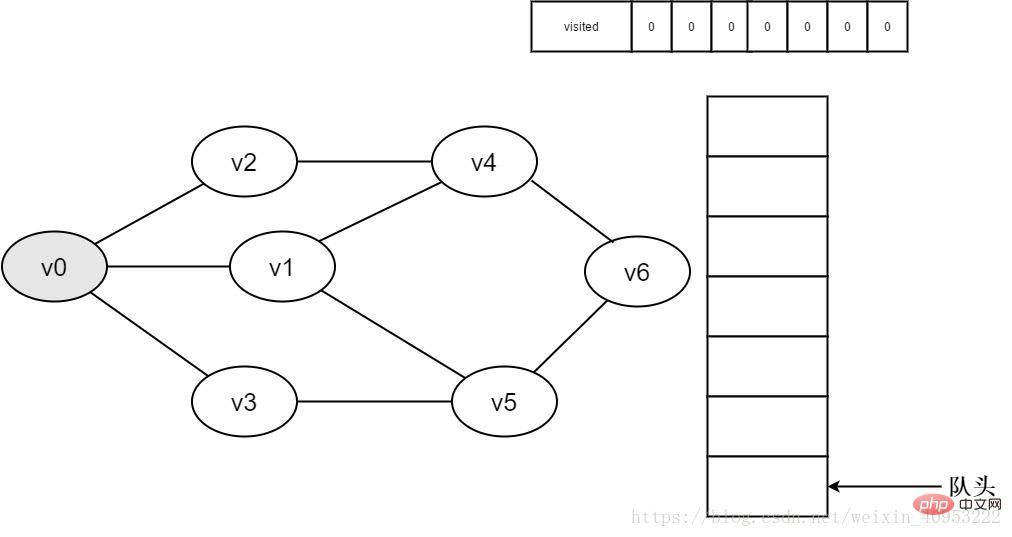
Figure 3-2-2
3. Visit vertex v0 and place visited[0 The value of ] is 1, and v0 is added to the queue at the same time.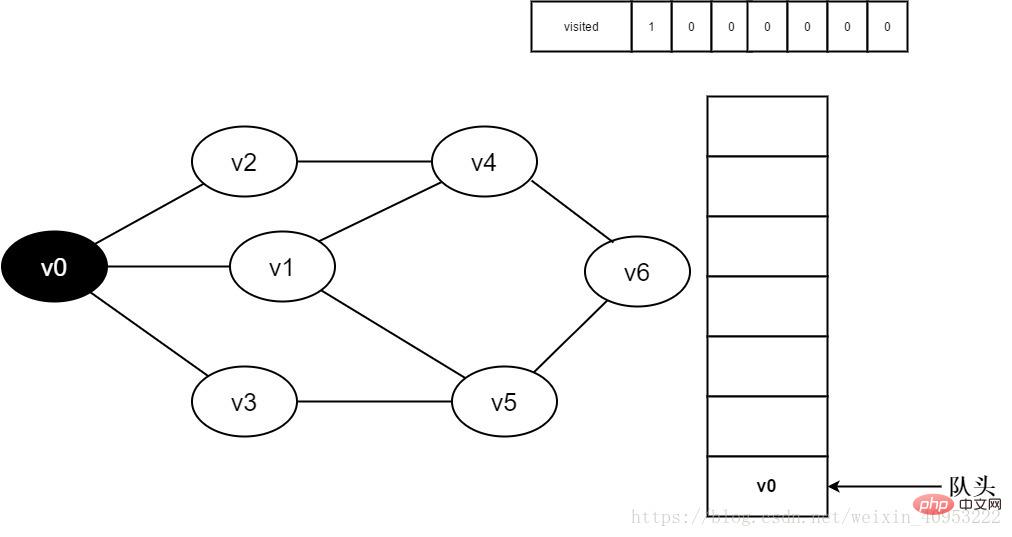
Figure 3-2-3
4. Dequeue v0 and visit v0’s adjacent point v2. Determine visited[2], because the value of visited[2] is 0, visit v2.
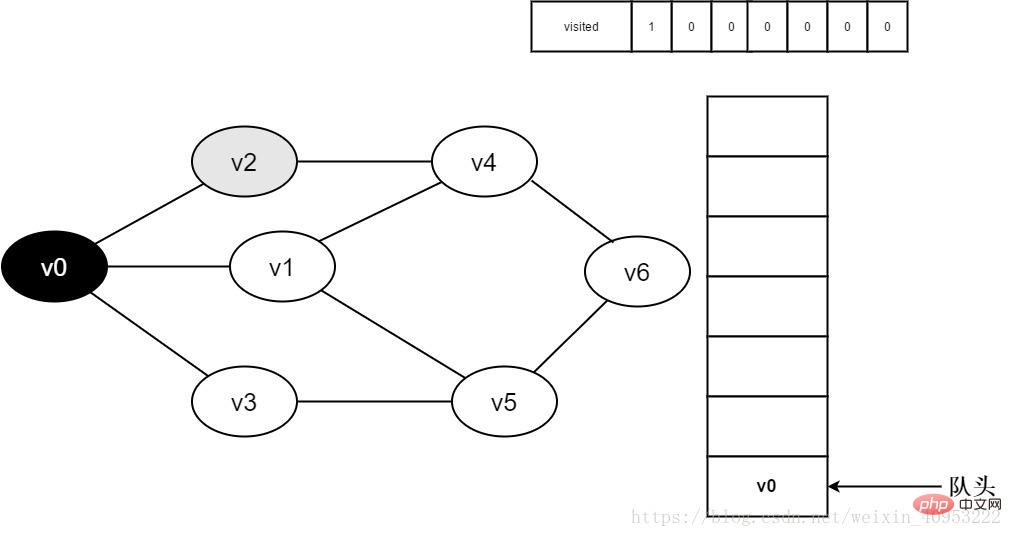
Figure 3-2-4
5. Set visited[2] to 1 and v2 Join the team.
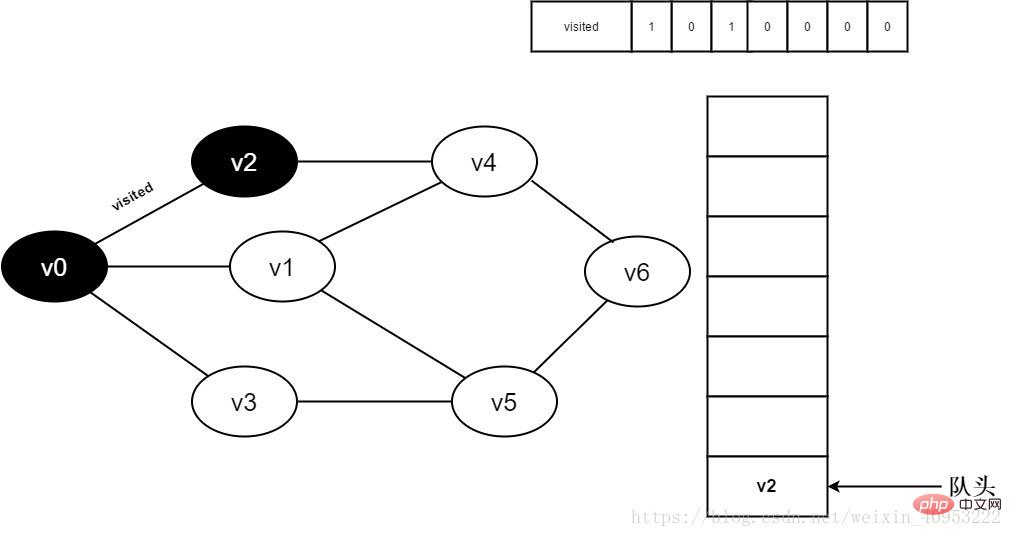
Figure 3-2-5
6. Access v0 neighbor point v1. Determine visited[1], because the value of visited[1] is 0, visit v1.
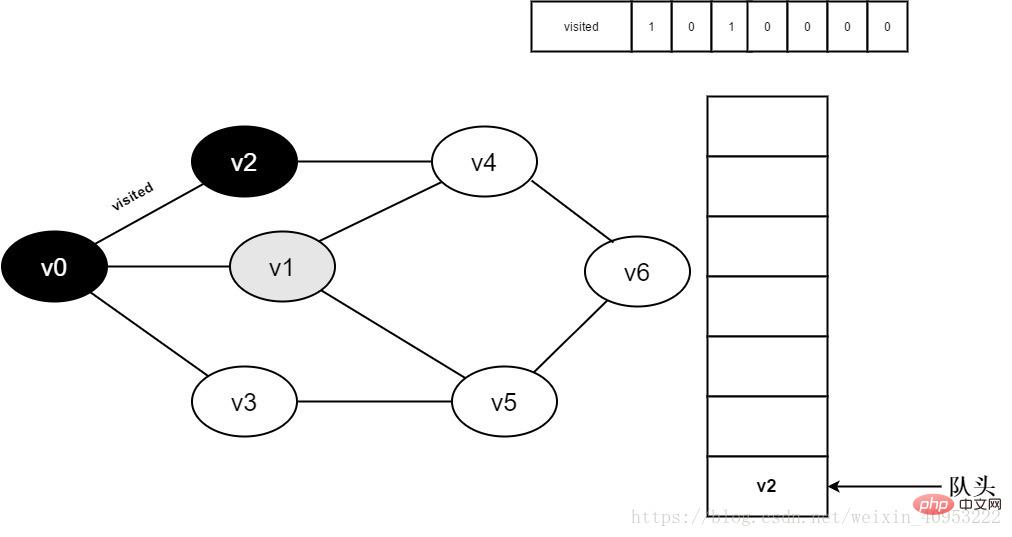
Figure 3-2-6
7. Set visited[1] to 0 and v1 Join the team.
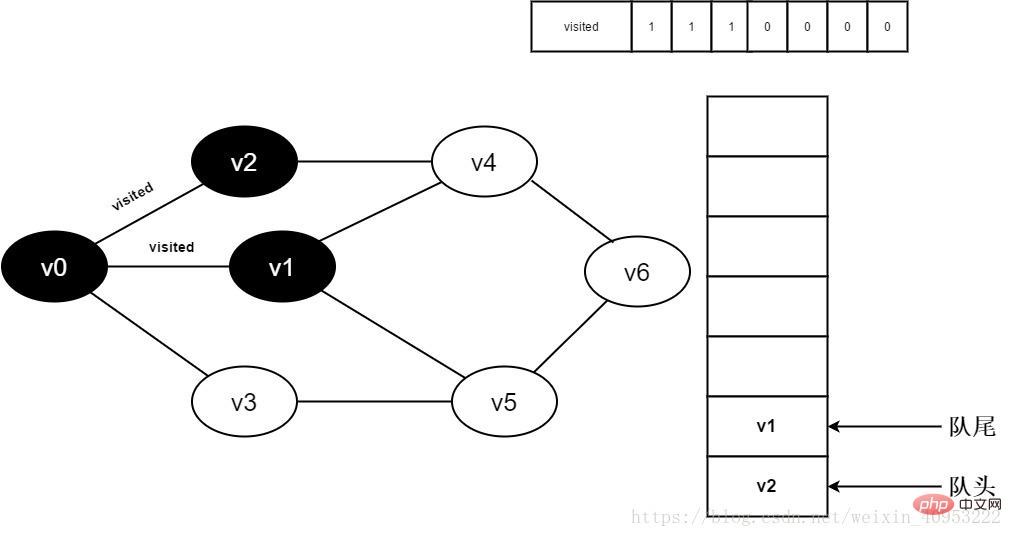
Figure 3-2-7
8. Judge visited[3] because its value is 0 , access v3. Set visited[3] to 0 and enqueue v3.
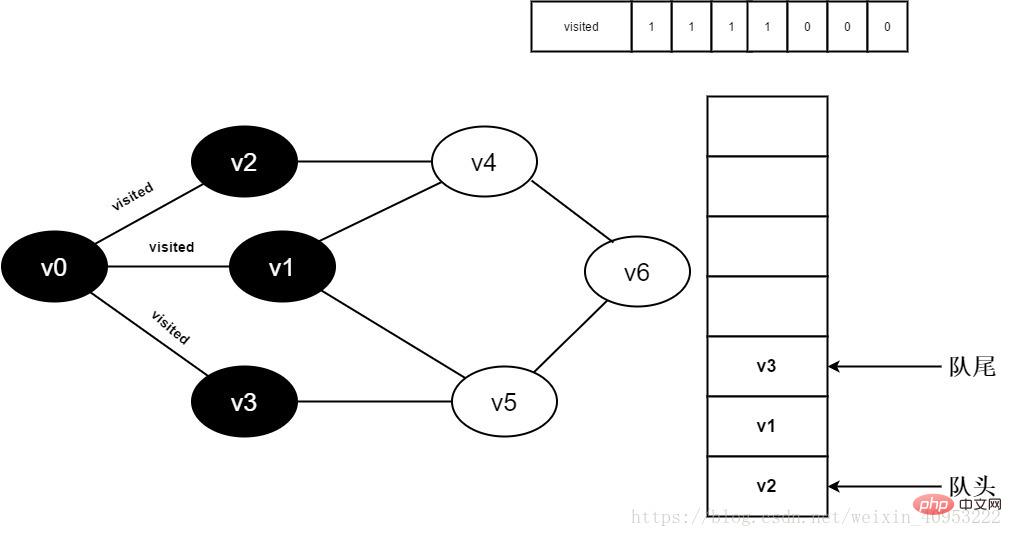
All adjacent points of Figure 3-2-8
9.v0 have been visited. Dequeue the head element v2 and start visiting all adjacent points of v2.
Start visiting v2 adjacent point v0, and judge visited[0]. Because its value is 1, no visit will be performed.
Continue to visit v2 adjacent point v4, judge visited[4], because its value is 0, visit v4, as shown below:
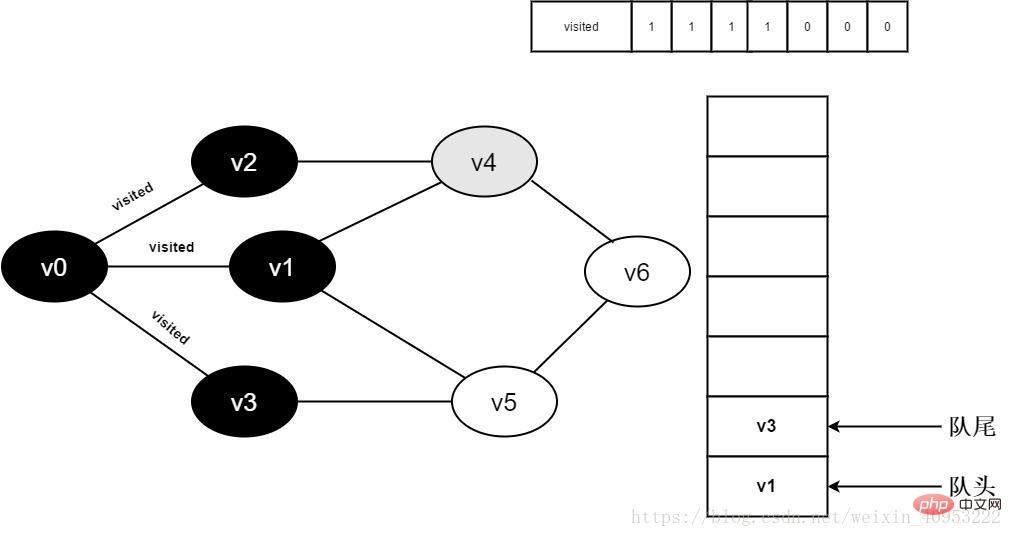
Figure 3-2-9
10. Set visited[4] to 1 and add v4 to the queue.
Figure 3-2-10
All adjacent points of 11.v2 have been visited. Dequeue the head element v1 and start visiting all adjacent points of v1.
Start visiting v1 adjacent point v0, because the visited[0] value is 1, no visit is performed.
Continue to visit v1 adjacent point v4, because the value of visited[4] is 1, no visit is performed.
Continue to visit v1 adjacent point v5, because the visited[5] value is 0, visit v5, as shown below:
Picture 3-2-11
12. Set visited[5] to 1 and add v5 to the queue.
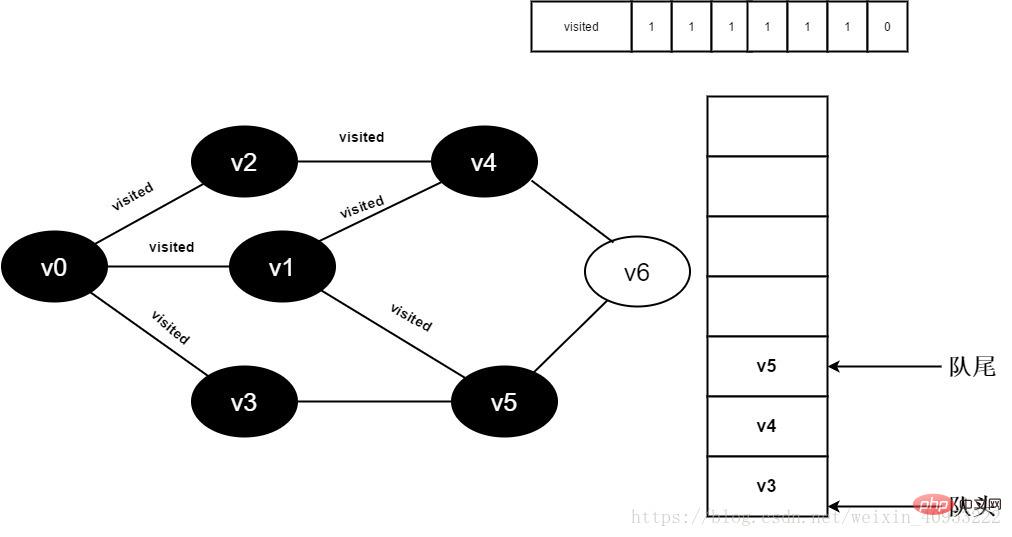
Figure 3-2-12
All adjacent points of 13.v1 have been visited, and the head element of the team v3 dequeues and starts accessing all adjacent points of v3.
Start visiting the v3 neighbor point v0. Because the visited[0] value is 1, no visit will be performed.
Continue to visit v3 neighbor point v5, because the visited[5] value is 1, no visit is performed.
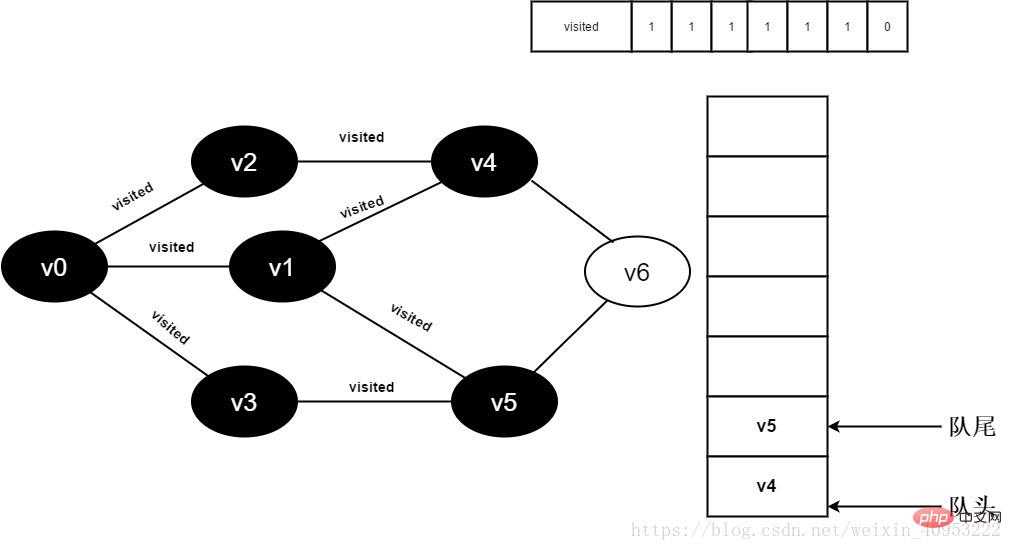
Figure 3-2-13
All adjacent points of 14.v3 have been visited, and The head element v4 is dequeued and begins to visit all adjacent points of v4.
Start visiting the adjacent point v2 of v4. Because the value of visited[2] is 1, no visit will be performed.
Continue to visit the adjacent point v6 of v4, because the value of visited[6] is 0, visit v6, as shown below:
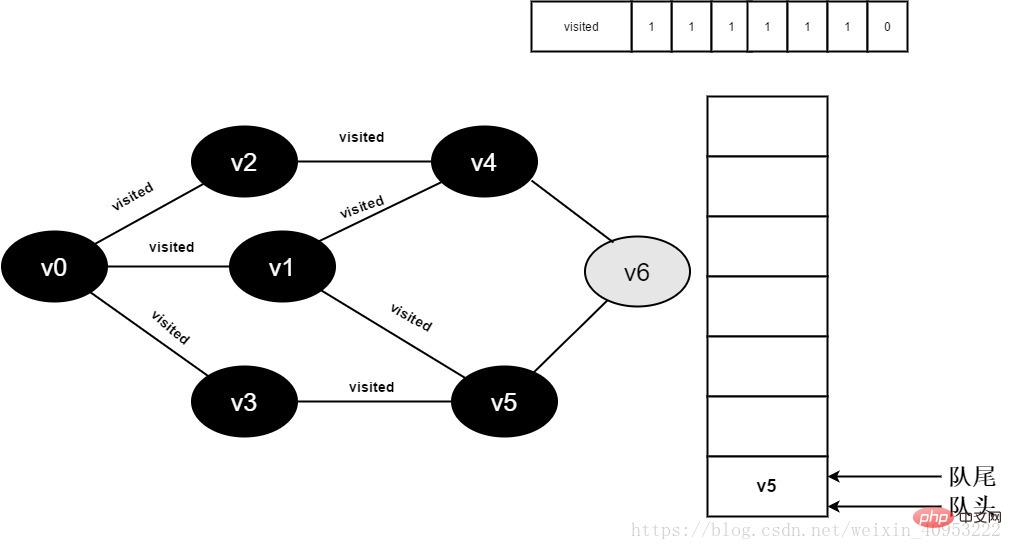
Figure 3-2-14
15. Set the value of visited[6] to 1 and add v6 to the queue.
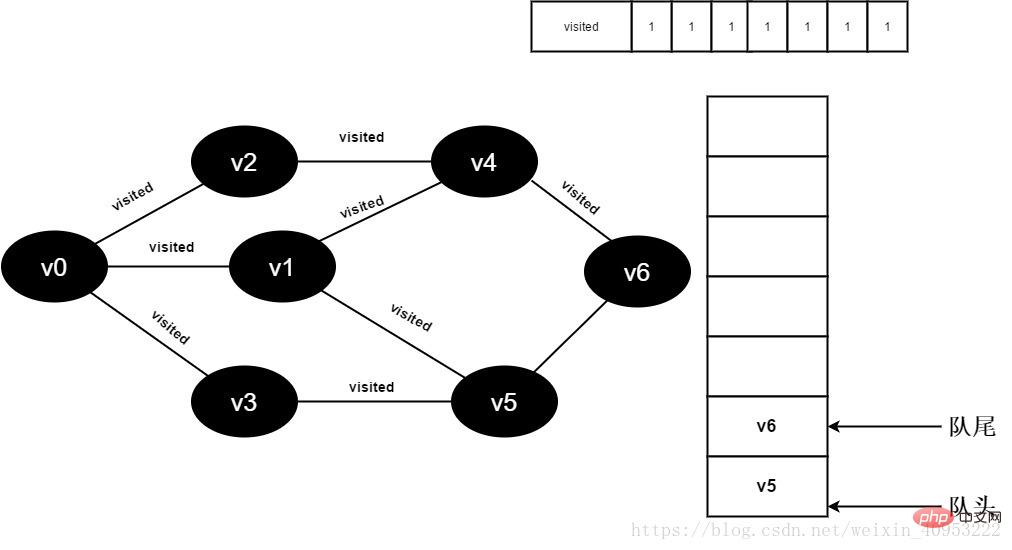
Figure 3-2-15
All adjacent points of 16.v4 have been visited. The head element v5 is dequeued and begins to visit all adjacent points of v5.
Start visiting v5 neighbor point v3. Because the value of visited[3] is 1, no visit will be performed.
Continue to visit v5 neighbor point v6, because the value of visited[6] is 1, no visit is performed.
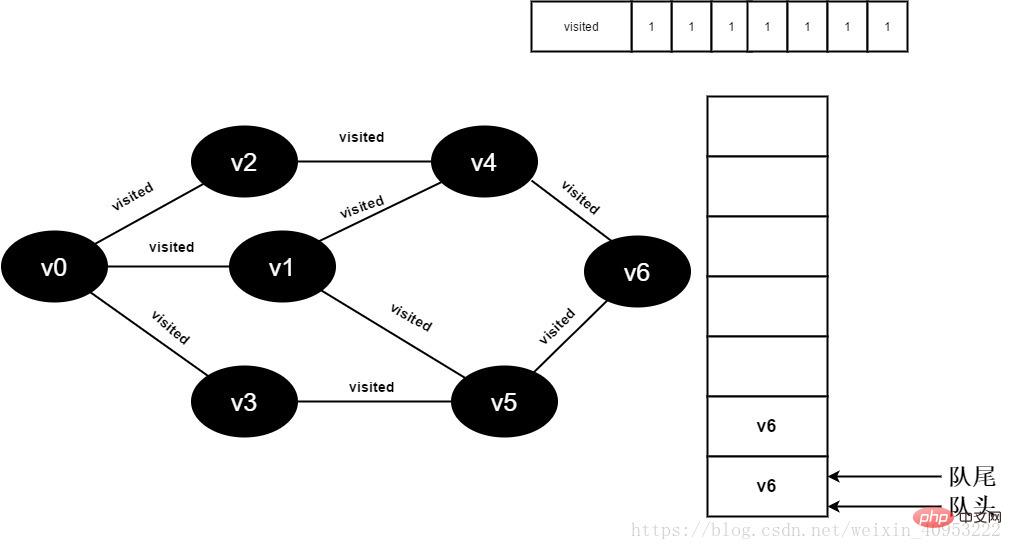
Figure 3-2-16
All adjacent points of 17.v5 have been visited. The head element v6 is dequeued and begins to visit all adjacent points of v6.
Start visiting v6 neighbor point v4. Because the value of visited[4] is 1, no visit will be performed.
Continue to visit the v6 neighbor point v5. Because the value of visited[5] is 1, no visit will be performed.
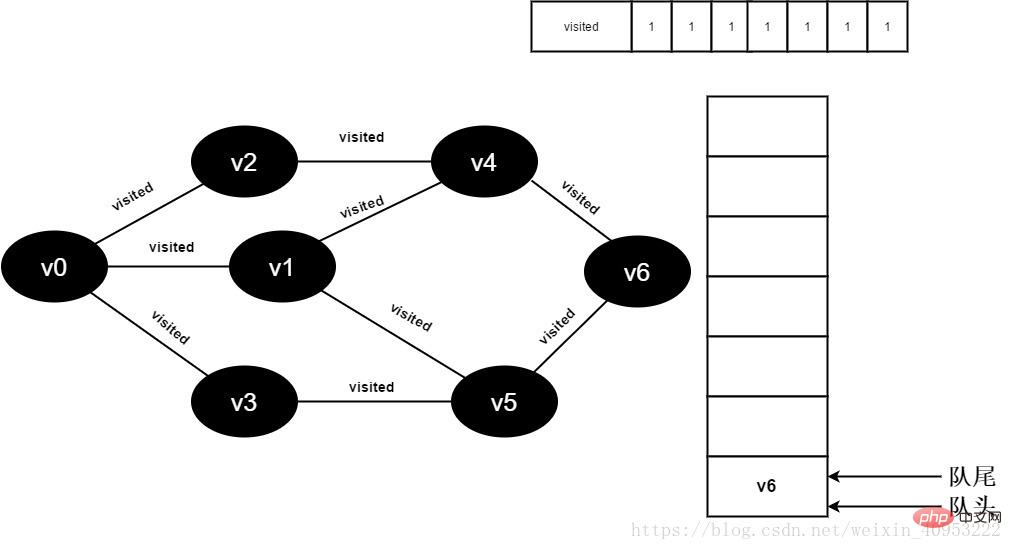
Figure 3-2-17
18. The queue is empty, exit the loop, and all vertices have been visited.
##Figure 3-2-18
3.3 Details Implementation of the code3.3.1 Use the adjacency matrix to represent the breadth-first search of the graph/*一些量的定义*/ queue<char> q; //定义一个队列，使用库函数queue #define MVNum 100 //表示最大顶点个数 bool visited[MVNum]; //定义一个visited数组，记录已被访问的顶点
/*邻接矩阵存储表示*/
typedef struct AMGraph
{
char vexs[MVNum]; //顶点表
int arcs[MVNum][MVNum]; //邻接矩阵
int vexnum, arcnum; //当前的顶点数和边数
}
AMGraph;/*找到顶点v的对应下标*/
int LocateVex(AMGraph &G, char v)
{
int i;
for (i = 0; i < G.vexnum; i++)
if (G.vexs[i] == v)
return i;
}/*采用邻接矩阵表示法，创建无向图G*/
int CreateUDG_1(AMGraph &G)
{
int i, j, k;
char v1, v2;
scanf("%d%d", &G.vexnum, &G.arcnum); //输入总顶点数，总边数
getchar(); //获取'\n’，防止其对之后的字符输入造成影响
for (i = 0; i < G.vexnum; i++)
scanf("%c", &G.vexs[i]); //依次输入点的信息
for (i = 0; i < G.vexnum; i++)
for (j = 0; j < G.vexnum; j++)
G.arcs[i][j] = 0; //初始化邻接矩阵边，0表示顶点i和j之间无边
for (k = 0; k < G.arcnum; k++)
{
getchar();
scanf("%c%c", &v1, &v2); //输入一条边依附的顶点
i = LocateVex(G, v1); //找到顶点i的下标
j = LocateVex(G, v2); //找到顶点j的下标
G.arcs[i][j] = G.arcs[j][i] = 1; //1表示顶点i和j之间有边，无向图不区分方向
}
return 1;
}/*采用邻接矩阵表示图的广度优先遍历*/
void BFS_AM(AMGraph &G,char v0)
{
/*从v0元素开始访问图*/
int u,i,v,w;
v = LocateVex(G,v0); //找到v0对应的下标
printf("%c ", v0); //打印v0
visited[v] = 1; //顶点v0已被访问
q.push(v0); //将v0入队
while (!q.empty())
{
u = q.front(); //将队头元素u出队，开始访问u的所有邻接点
v = LocateVex(G, u); //得到顶点u的对应下标
q.pop(); //将顶点u出队
for (i = 0; i < G.vexnum; i++)
{
w = G.vexs[i];
if (G.arcs[v][i] && !visited[i])//顶点u和w间有边，且顶点w未被访问
{
printf("%c ", w); //打印顶点w
q.push(w); //将顶点w入队
visited[i] = 1; //顶点w已被访问
}
}
}
}/*找到顶点对应的下标*/
int LocateVex(ALGraph &G, char v)
{
int i;
for (i = 0; i < G.vexnum; i++)
if (v == G.vertices[i].data)
return i;
}/*邻接表存储表示*/
typedef struct ArcNode //边结点
{
int adjvex; //该边所指向的顶点的位置
ArcNode *nextarc; //指向下一条边的指针
int info; //和边相关的信息，如权值
}ArcNode;
typedef struct VexNode //表头结点
{
char data;
ArcNode *firstarc; //指向第一条依附该顶点的边的指针
}VexNode,AdjList[MVNum]; //AbjList表示一个表头结点表
typedef struct ALGraph
{
AdjList vertices;
int vexnum, arcnum;
}ALGraph;/*采用邻接表表示法，创建无向图G*/
int CreateUDG_2(ALGraph &G)
{
int i, j, k;
char v1, v2;
scanf("%d%d", &G.vexnum, &G.arcnum); //输入总顶点数，总边数
getchar();
for (i = 0; i < G.vexnum; i++) //输入各顶点，构造表头结点表
{
scanf("%c", &G.vertices[i].data); //输入顶点值
G.vertices[i].firstarc = NULL; //初始化每个表头结点的指针域为NULL
}
for (k = 0; k < G.arcnum; k++) //输入各边，构造邻接表
{
getchar();
scanf("%c%c", &v1, &v2); //输入一条边依附的两个顶点
i = LocateVex(G, v1); //找到顶点i的下标
j = LocateVex(G, v2); //找到顶点j的下标
ArcNode *p1 = new ArcNode; //创建一个边结点*p1
p1->adjvex = j; //其邻接点域为j
p1->nextarc = G.vertices[i].firstarc; G.vertices[i].firstarc = p1; // 将新结点*p插入到顶点v1的边表头部
ArcNode *p2 = new ArcNode; //生成另一个对称的新的表结点*p2
p2->adjvex = i;
p2->nextarc = G.vertices[j].firstarc;
G.vertices[j].firstarc = p1;
}
return 1;
}/*采用邻接表表示图的广度优先遍历*/
void BFS_AL(ALGraph &G, char v0)
{
int u,w,v;
ArcNode *p;
printf("%c ", v0); //打印顶点v0
v = LocateVex(G, v0); //找到v0对应的下标
visited[v] = 1; //顶点v0已被访问
q.push(v0); //将顶点v0入队
while (!q.empty())
{
u = q.front(); //将顶点元素u出队，开始访问u的所有邻接点
v = LocateVex(G, u); //得到顶点u的对应下标
q.pop(); //将顶点u出队
for (p = G.vertices[v].firstarc; p; p = p->nextarc) //遍历顶点u的邻接点
{
w = p->adjvex;
if (!visited[w]) //顶点p未被访问
{
printf("%c ", G.vertices[w].data); //打印顶点p
visited[w] = 1; //顶点p已被访问
q.push(G.vertices[w].data); //将顶点p入队
}
}
}
}/*广度优先搜索非连通图*/
void BFSTraverse(AMGraph G)
{
int v;
for (v = 0; v < G.vexnum; v++)
visited[v] = 0; //将visited数组初始化
for (v = 0; v < G.vexnum; v++)
if (!visited[v]) BFS_AM(G, G.vexs[v]); //对尚未访问的顶点调用BFS
}
Figure 4-2-1
Figure 4-2-2
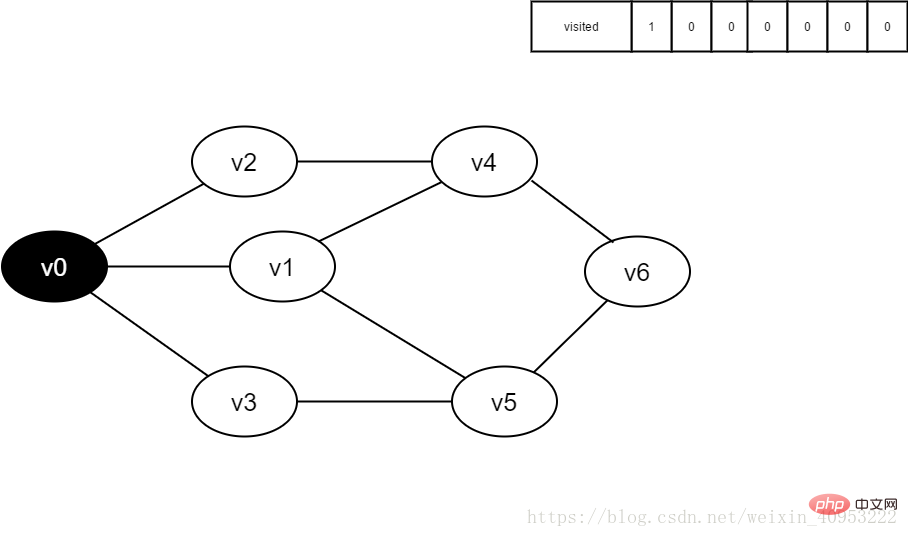
Figure 4-2-3
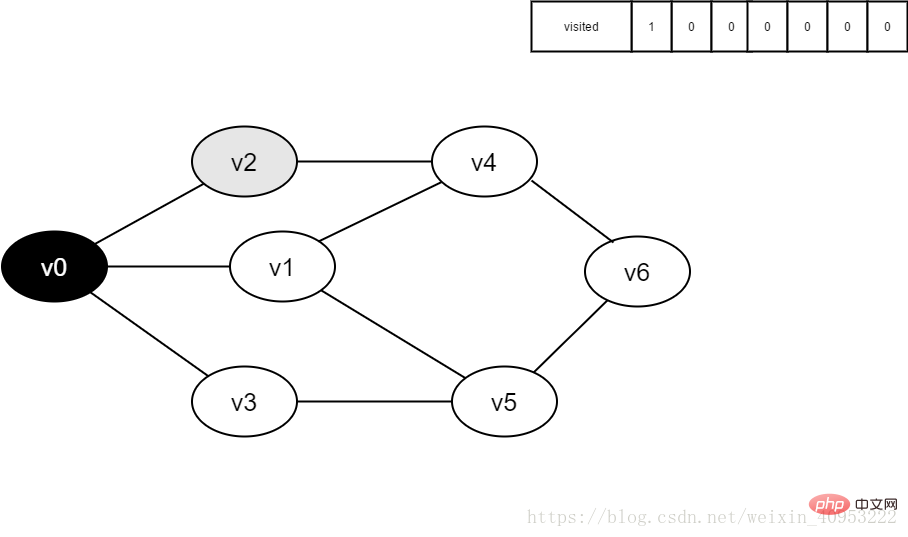
Figure 4-2-4
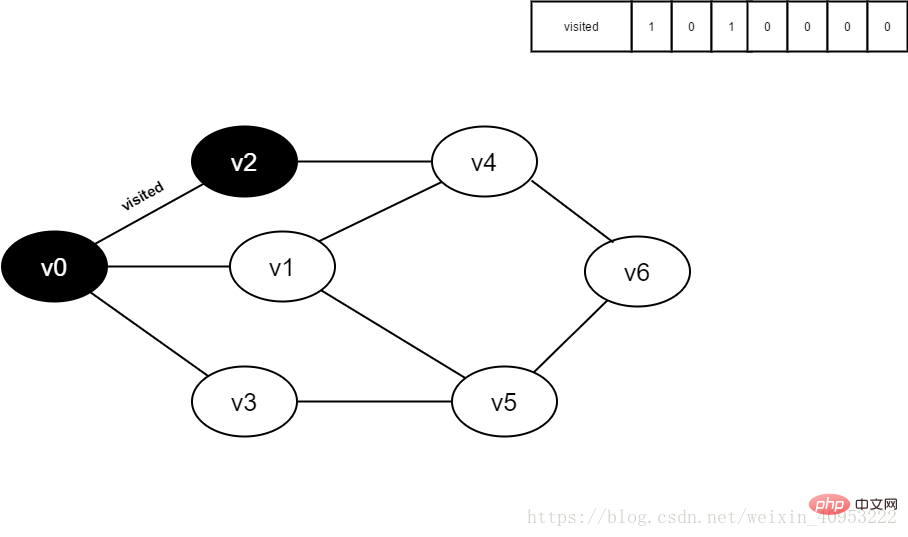
Figure 4-2-5
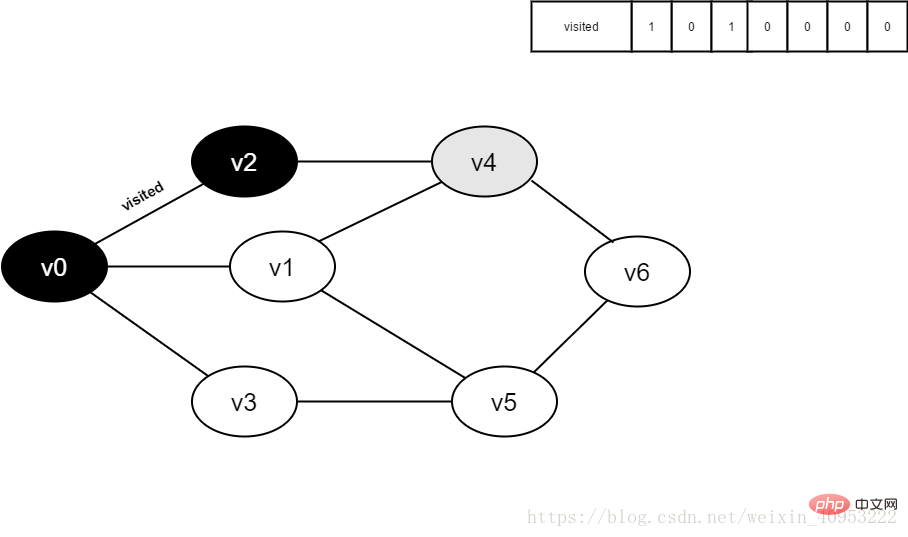
Figure 4-2-6
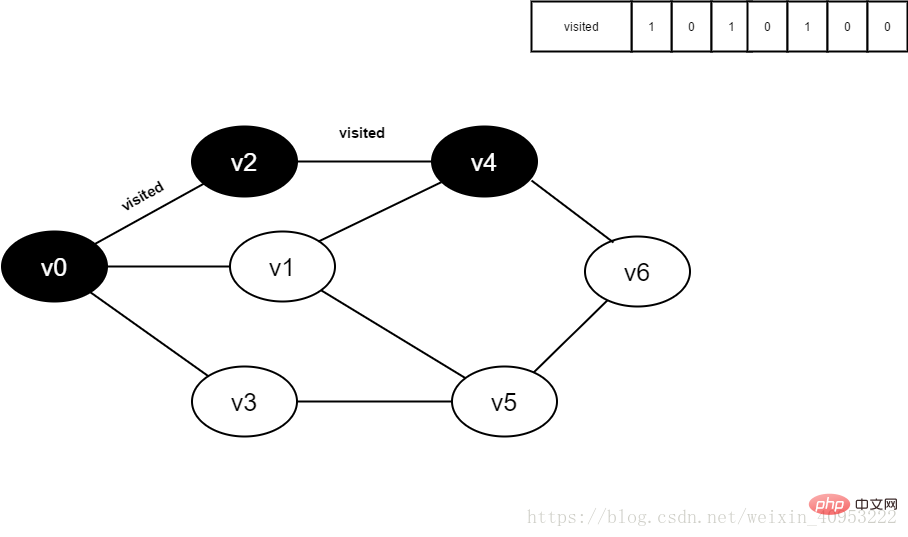
Figure 4-2-7
8. Visit the adjacent point v1 of v4, determine visited[1], and its value is 0, access v1.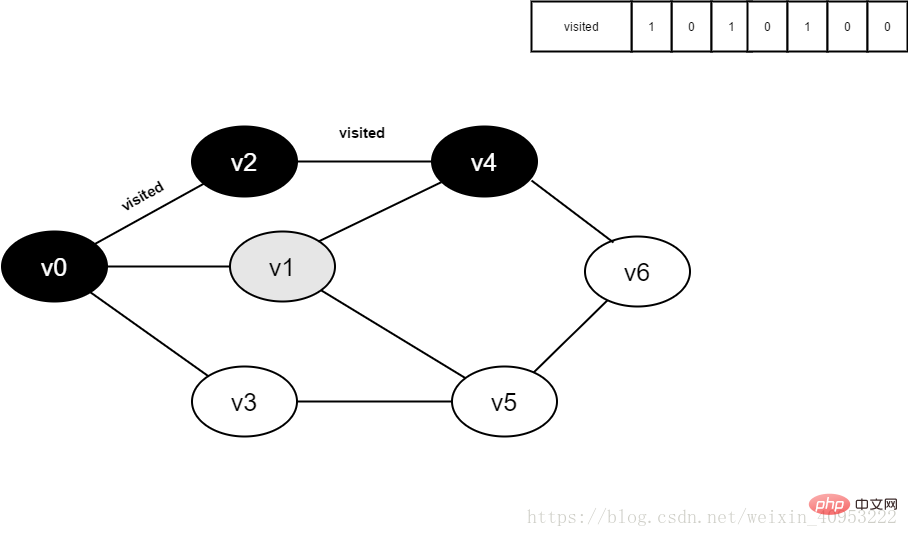
Figure 4-2-8
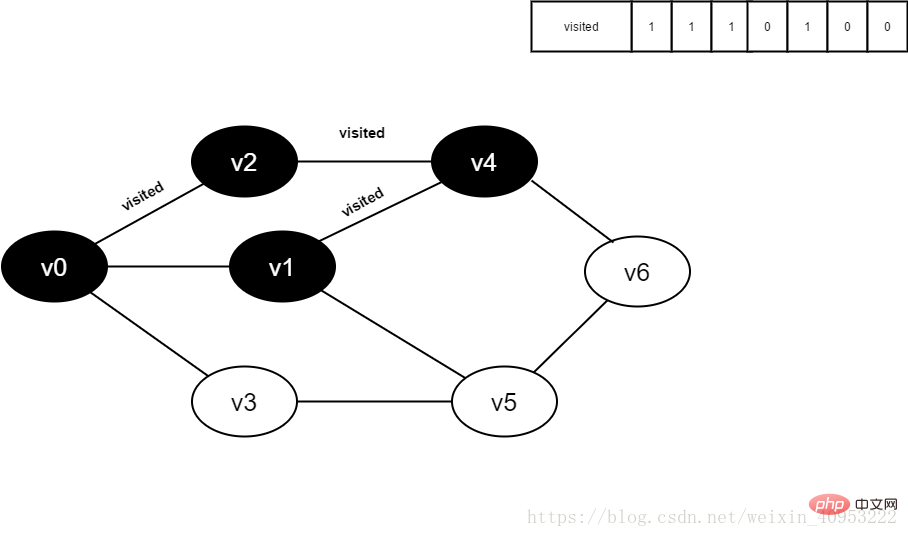
Figure 4-2-9
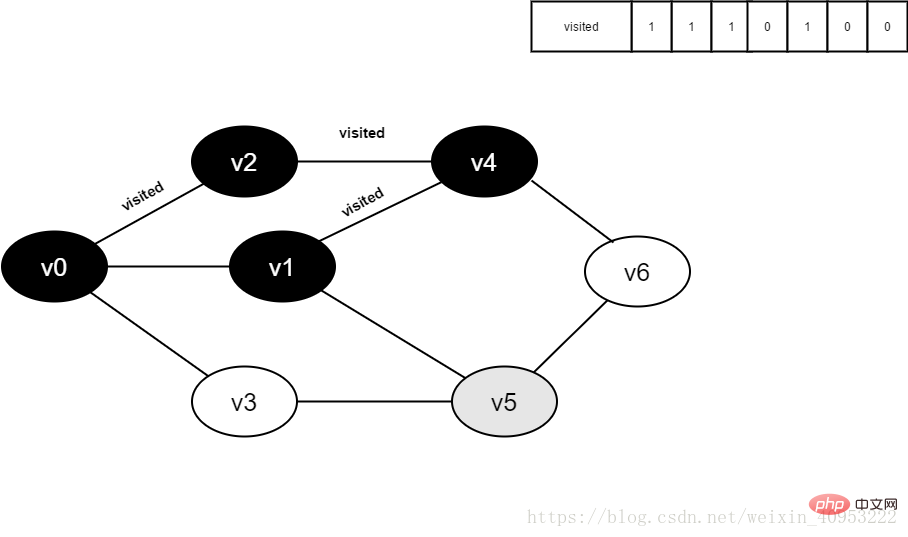
Figure 4-2-10
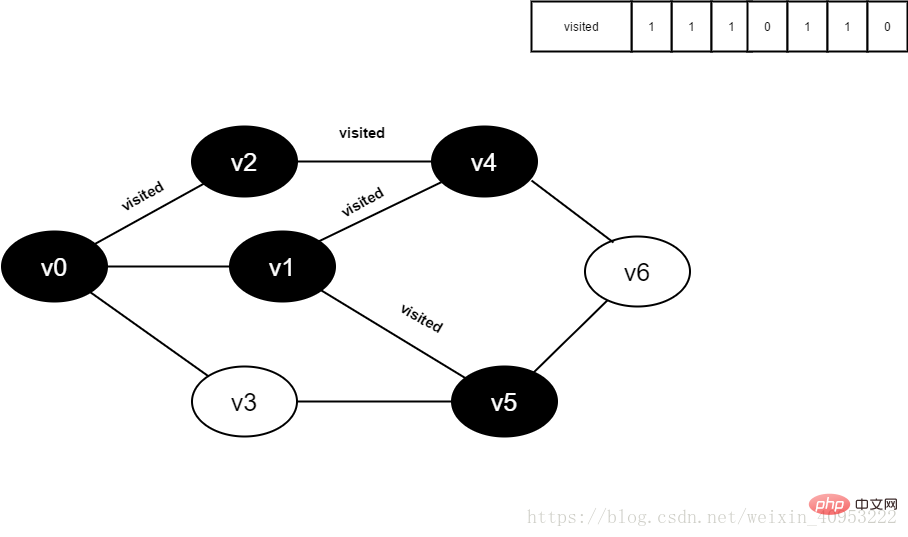
Figure 4-2-11
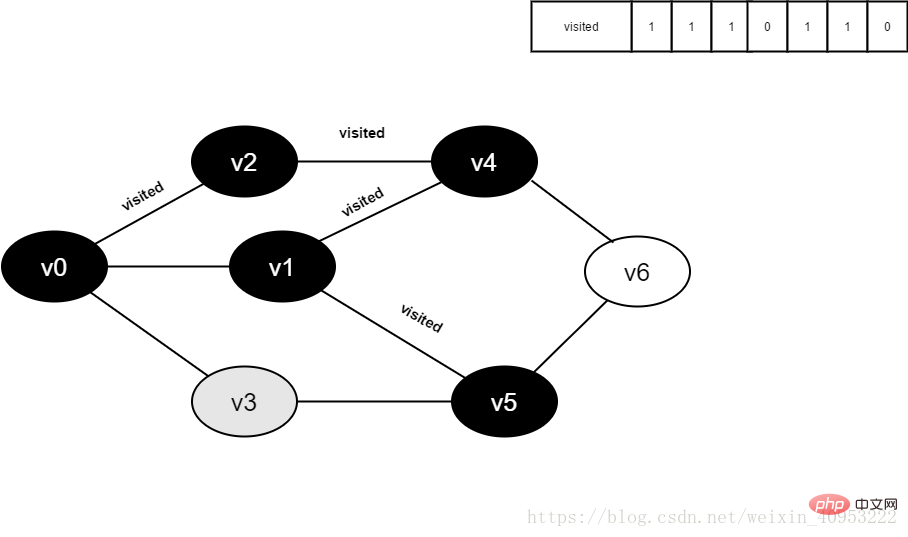
图4-2-12
13.将visited[1]置为1。
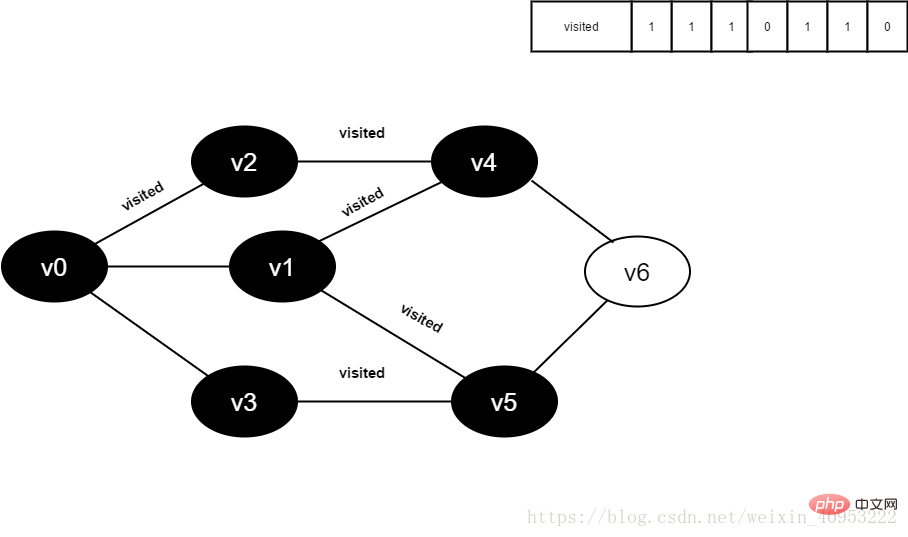
图4-2-13
14.访问v3的邻接点v0，判断visited[0]，其值为1，不访问。
继续访问v3的邻接点v5，判断visited[5]，其值为1，不访问。
v3所有邻接点均已被访问，回溯到其上一个顶点v5，遍历v5所有邻接点。
访问v5的邻接点v6，判断visited[6]，其值为0，访问v6。
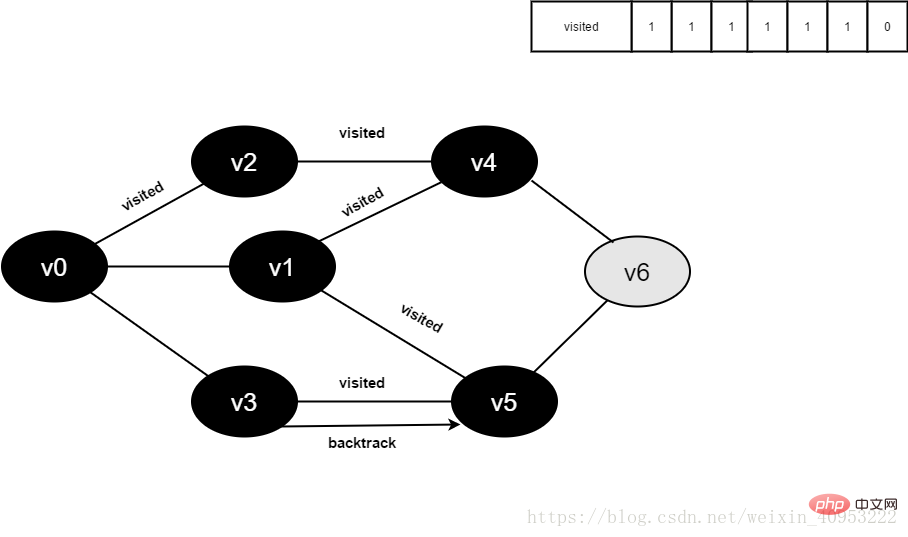
图4-2-14
15.将visited[6]置为1。
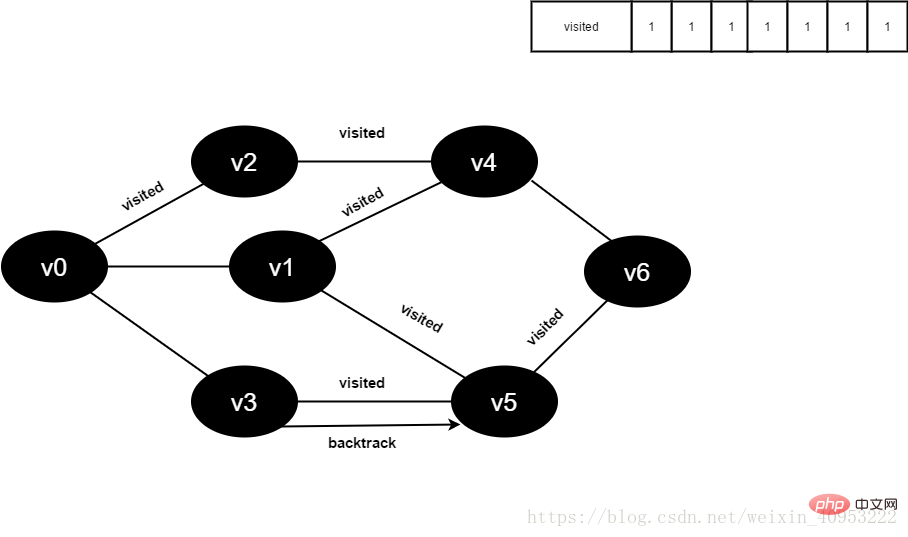
图4-2-15
16.访问v6的邻接点v4，判断visited[4]，其值为1，不访问。
访问v6的邻接点v5，判断visited[5]，其值为1，不访问。
v6所有邻接点均已被访问，回溯到其上一个顶点v5，遍历v5剩余邻接点。
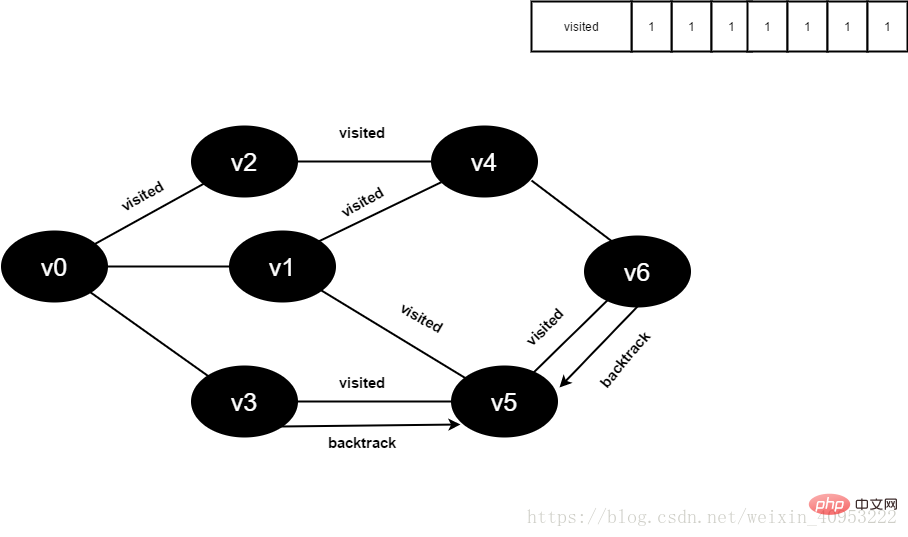
图4-2-16
17.v5所有邻接点均已被访问，回溯到其上一个顶点v1。
v1所有邻接点均已被访问，回溯到其上一个顶点v4，遍历v4剩余邻接点v6。
v4所有邻接点均已被访问，回溯到其上一个顶点v2。
v2所有邻接点均已被访问，回溯到其上一个顶点v1，遍历v1剩余邻接点v3。
v1所有邻接点均已被访问，搜索结束。
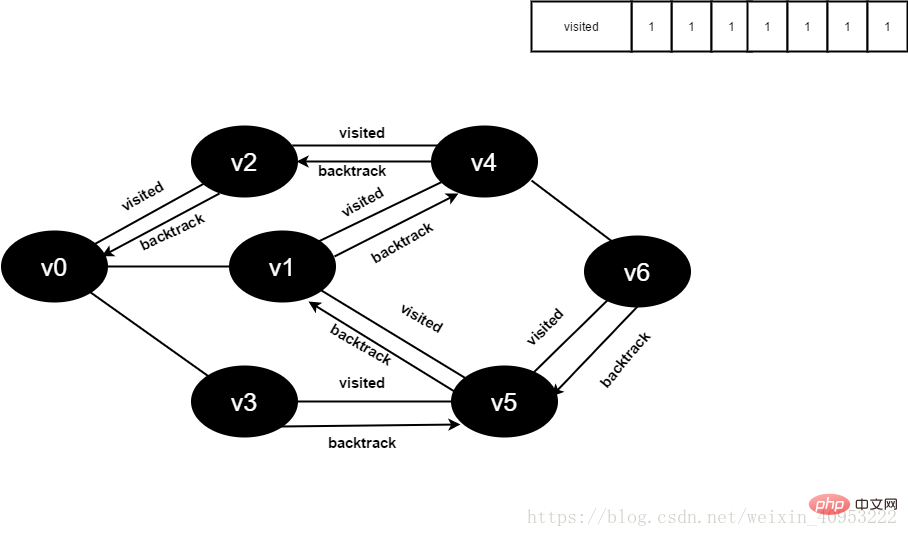
图4-2-17
邻接矩阵的创建在上述已描述过，这里不再赘述
void DFS_AM(AMGraph &G, int v)
{
int w;
printf("%c ", G.vexs[v]);
visited[v] = 1;
for (w = 0; w < G.vexnum; w++)
if (G.arcs[v][w]&&!visited[w]) //递归调用
DFS_AM(G,w);
}邻接表的创建在上述已描述过，这里不再赘述。
void DFS_AL(ALGraph &G, int v)
{
int w;
printf("%c ", G.vertices[v].data);
visited[v] = 1;
ArcNode *p = new ArcNode;
p = G.vertices[v].firstarc;
while (p)
{
w = p->adjvex;
if (!visited[w]) DFS_AL(G, w);
p = p->nextarc;
}
}更多相关知识，请访问：PHP中文网！
The above is the detailed content of What is breadth-first traversal of a graph similar to a binary tree?. For more information, please follow other related articles on the PHP Chinese website!
How to close port 445 in xp
How to use the Print() function in Python
Solution to the Invalid Partition Table prompt when Windows 10 starts up
How to make gif animation in ps
css background code collection
Data encryption storage measures
How to check website dead links
The difference between server and cloud host
![[Web front-end] Node.js quick start](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
