Detailed method for finding the roots of a quadratic equation using Geometry Sketchpad

Geometry Sketchpad Find the roots of quadratic equations. Solving quadratic equations is a common problem in mathematics. Geometry Sketchpad, a geometric drawing software, provides an effective way to solve such equations. In this article, PHP editor Baicao will introduce in detail the complete process of using the geometric sketchpad to find the roots of a quadratic equation of one variable. This article will demonstrate step by step how to construct the graph of an equation, exploit geometric properties, and derive the exact values ​​of the roots. Readers are advised to read the following details carefully to master the specific steps and techniques of this method.

Step 1: Open the software and establish three parameters. Click [Data] in the upper menu and select [New Parameter] from the pop-up drop-down menu. In the small window that pops up, change t1 to a, select unitless, and default the value, then click OK. In the same way, establish the other two parameters b and parameter c. Let their values ​​​​be 1 first, and then you can change the values ​​​​of the parameters at will.

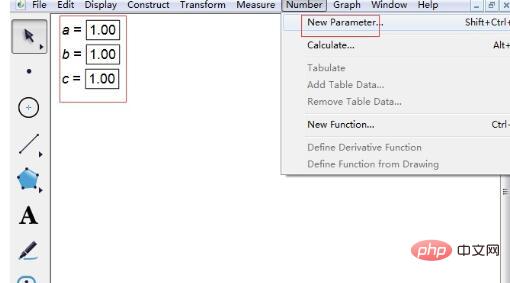
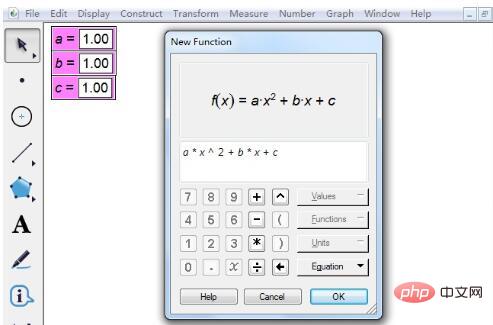
Step 2 Enter the function expression of the quadratic equation. Click [Draw] on the upper menu, select the draw new function option, and enter the expression in the pop-up dialog box. There are a few points to note when entering expressions. 1. When entering parameter a, click the parameter a in the upper left corner with the mouse to enter. Then click the multiplication sign * to enter x. The same goes for other parameters.

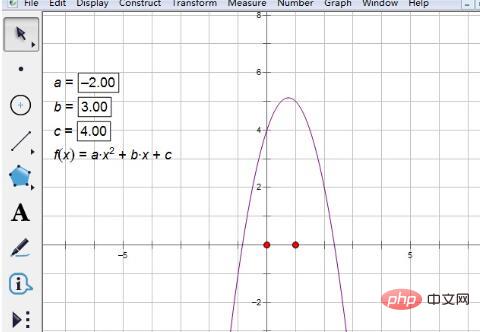
Step 3 Change parameter values. After entering the expression, click [OK] to draw a graph as shown below. Obviously, it has no intersection with the horizontal axis, and the corresponding quadratic equation has no real roots. So to change the value of the parameter, double-click parameter a, and a small window will pop up. Just enter the specific value. The same goes for other parameters.

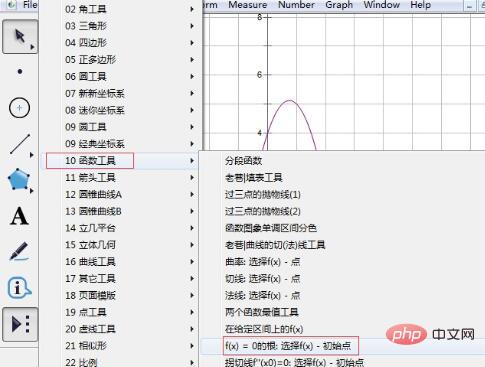
Step 4 Select the function tool. Click the [Custom Tool] button on the left toolbar, and select [Function Tool] from the pop-up shortcut option - the root of f(x)=0.

Step 5 Find the roots of the equation. Click the function analysis expression once, move the cursor, and the root label appears, and one root is displayed. Click the expression again, move the cursor, another root label appears, and the second root is displayed.

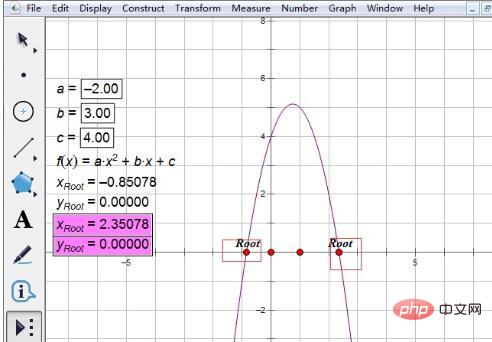
Tips: In this way, the two real roots of the quadratic equation have been found. Note that the two x values ​​are the roots, and y is the ordinate. So how to find the roots of a quadratic equation with arbitrary coefficients? The method is very simple. You just need to double-click the parameters, change the values ​​of a, b, and c, and the roots of the new equation will be displayed immediately.

The above is the detailed content of Detailed method for finding the roots of a quadratic equation using Geometry Sketchpad. For more information, please follow other related articles on the PHP Chinese website!