
The content of this article is to share with you distance measurement and python implementation. Friends in need can refer to the content in the article
##Reprinted from: http://www.cnblogs.com/denny402/p/7027954.html
https://www.cnblogs.com/denny402/p /7028832.html
1. Euclidean Distance Euclidean distance is the easiest to understand distance calculation method, derived from Euclidean space The distance formula between two points.
(1) The Euclidean distance between two points a(x1,y1) and b(x2,y2) on the two-dimensional plane: 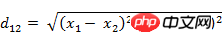 (2) Two points a(x1) in the three-dimensional space ,y1,z1) and b(x2,y2,z2) Euclidean distance:
(2) Two points a(x1) in the three-dimensional space ,y1,z1) and b(x2,y2,z2) Euclidean distance: 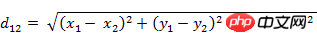 (3) Two n-dimensional vectors a(x11,x12,…,x1n) and b( The Euclidean distance between x21, Implementation:
(3) Two n-dimensional vectors a(x11,x12,…,x1n) and b( The Euclidean distance between x21, Implementation:
Method 1: 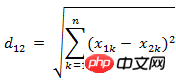

##
import numpy as np x=np.random.random(10) y=np.random.random(10)#方法一:根据公式求解d1=np.sqrt(np.sum(np.square(x-y)))#方法二:根据scipy库求解from scipy.spatial.distance import pdistX=np.vstack([x,y]) d2=pdist(X)
(2) Two n-dimensional vectors a(x11,x12) ,...,x1n) and b(x21,x22,...,x2n)
Implementation in python:

import numpy as np x=np.random.random(10) y=np.random.random(10)#方法一:根据公式求解d1=np.sum(np.abs(x-y))#方法二:根据scipy库求解from scipy.spatial.distance import pdistX=np.vstack([x,y]) d2=pdist(X,'cityblock')
Another equivalent form of this formula is
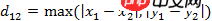 Implementation in python:
Implementation in python:

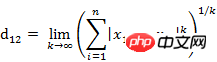
##
import numpy as np x=np.random.random(10) y=np.random.random(10)#方法一:根据公式求解d1=np.max(np.abs(x-y))#方法二:根据scipy库求解from scipy.spatial.distance import pdistX=np.vstack([x,y]) d2=pdist(X,'chebyshev')
4. 闵可夫斯基距离(Minkowski Distance)
闵氏距离不是一种距离,而是一组距离的定义。
(1) 闵氏距离的定义
两个n维变量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的闵可夫斯基距离定义为:
也可写成

其中p是一个变参数。
当p=1时,就是曼哈顿距离
当p=2时,就是欧氏距离
当p→∞时,就是切比雪夫距离
根据变参数的不同,闵氏距离可以表示一类的距离。
(2)闵氏距离的缺点
闵氏距离,包括曼哈顿距离、欧氏距离和切比雪夫距离都存在明显的缺点。
举个例子:二维样本(身高,体重),其中身高范围是150~190,体重范围是50~60,有三个样本:a(180,50),b(190,50),c(180,60)。那么a与b之间的闵氏距离(无论是曼哈顿距离、欧氏距离或切比雪夫距离)等于a与c之间的闵氏距离,但是身高的10cm真的等价于体重的10kg么?因此用闵氏距离来衡量这些样本间的相似度很有问题。
简单说来,闵氏距离的缺点主要有两个:(1)将各个分量的量纲(scale),也就是“单位”当作相同的看待了。(2)没有考虑各个分量的分布(期望,方差等)可能是不同的。
python中的实现:
import numpy as np x=np.random.random(10) y=np.random.random(10)#方法一:根据公式求解,p=2d1=np.sqrt(np.sum(np.square(x-y)))#方法二:根据scipy库求解from scipy.spatial.distance import pdistX=np.vstack([x,y]) d2=pdist(X,'minkowski',p=2)
5. 标准化欧氏距离 (Standardized Euclidean distance )
(1)标准欧氏距离的定义
标准化欧氏距离是针对简单欧氏距离的缺点而作的一种改进方案。标准欧氏距离的思路:既然数据各维分量的分布不一样,好吧!那我先将各个分量都“标准化”到均值、方差相等吧。均值和方差标准化到多少呢?这里先复习点统计学知识吧,假设样本集X的均值(mean)为m,标准差(standard deviation)为s,那么X的“标准化变量”表示为: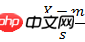
标准化后的值 = ( 标准化前的值 - 分量的均值 ) /分量的标准差
经过简单的推导就可以得到两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的标准化欧氏距离的公式:
如果将方差的倒数看成是一个权重,这个公式可以看成是一种加权欧氏距离(Weighted Euclidean distance)。
python中的实现:
import numpy as np x=np.random.random(10) y=np.random.random(10) X=np.vstack([x,y])#方法一:根据公式求解sk=np.var(X,axis=0,ddof=1) d1=np.sqrt(((x - y) ** 2 /sk).sum())#方法二:根据scipy库求解from scipy.spatial.distance import pdistd2=pdist(X,'seuclidean')
6. 马氏距离(Mahalanobis Distance)
(1)马氏距离定义
有M个样本向量X1~Xm,协方差矩阵记为S,均值记为向量μ,则其中样本向量X到u的马氏距离表示为:
而其中向量Xi与Xj之间的马氏距离定义为: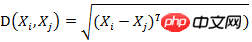
若协方差矩阵是单位矩阵(各个样本向量之间独立同分布),则公式就成了: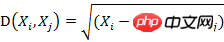
也就是欧氏距离了。
若协方差矩阵是对角矩阵,公式变成了标准化欧氏距离。
python 中的实现:
import numpy as np x=np.random.random(10) y=np.random.random(10)#马氏距离要求样本数要大于维数,否则无法求协方差矩阵#此处进行转置,表示10个样本,每个样本2维X=np.vstack([x,y]) XT=X.T#方法一:根据公式求解S=np.cov(X) #两个维度之间协方差矩阵SI = np.linalg.inv(S) #协方差矩阵的逆矩阵#马氏距离计算两个样本之间的距离,此处共有10个样本,两两组合,共有45个距离。n=XT.shape[0] d1=[]for i in range(0,n): for j in range(i+1,n): delta=XT[i]-XT[j] d=np.sqrt(np.dot(np.dot(delta,SI),delta.T)) d1.append(d) #方法二:根据scipy库求解from scipy.spatial.distance import pdist d2=pdist(XT,'mahalanobis')
马氏优缺点:
1)马氏距离的计算是建立在总体样本的基础上的,这一点可以从上述协方差矩阵的解释中可以得出,也就是说,如果拿同样的两个样本,放入两个不同的总体中,最后计算得出的两个样本间的马氏距离通常是不相同的,除非这两个总体的协方差矩阵碰巧相同;
2)在计算马氏距离过程中,要求总体样本数大于样本的维数,否则得到的总体样本协方差矩阵逆矩阵不存在,这种情况下,用欧式距离计算即可。
3)还有一种情况,满足了条件总体样本数大于样本的维数,但是协方差矩阵的逆矩阵仍然不存在,比如三个样本点(3,4),(5,6)和(7,8),这种情况是因为这三个样本在其所处的二维空间平面内共线。这种情况下,也采用欧式距离计算。
4)在实际应用中“总体样本数大于样本的维数”这个条件是很容易满足的,而所有样本点出现3)中所描述的情况是很少出现的,所以在绝大多数情况下,马氏距离是可以顺利计算的,但是马氏距离的计算是不稳定的,不稳定的来源是协方差矩阵,这也是马氏距离与欧式距离的最大差异之处。
优点:它不受量纲的影响,两点之间的马氏距离与原始数据的测量单位无关;由标准化数据和中心化数据(即原始数据与均值之差)计算出的二点之间的马氏距离相同。马氏距离还可以排除变量之间的相关性的干扰。缺点:它的缺点是夸大了变化微小的变量的作用。
7. 夹角余弦(Cosine)
It can also be called cosine similarity. The cosine of the angle in geometry can be used to measure the difference between the directions of two vectors. This concept is borrowed in to measure the difference between sample vectors.
(1) The cosine formula of the angle between vector A(x1,y1) and vector B(x2,y2) in two-dimensional space: 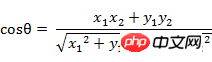
(2) Two n-dimensional sample points The cosine of the angle between a(x11,x12,…,x1n) and b(x21,x22,…,x2n)
Similarly, for two n-dimensional sample points a(x11,x12,…,x1n) and b (x21,x22,…,x2n), you can use a concept similar to the cosine of the angle to measure the degree of similarity between them. 
That is: 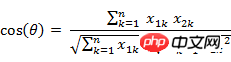
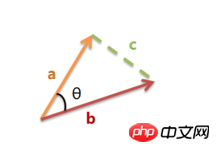
The value range of cosine is [-1,1]. Find the angle between the two vectors and obtain the cosine value corresponding to the angle. This cosine value can be used to characterize the similarity of the two vectors. The smaller the angle is, approaching 0 degrees, the closer the cosine value is to 1, and the more consistent their directions are, the more similar they are. When the directions of two vectors are completely opposite, the cosine of the angle between them takes the minimum value -1. When the cosine value is 0, the two vectors are orthogonal and the included angle is 90 degrees. Therefore, it can be seen that cosine similarity has nothing to do with the magnitude of the vector, but only with the direction of the vector.
import numpy as np x=np.random.random(10) y=np.random.random(10)#方法一:根据公式求解d1=np.dot(x,y)/(np.linalg.norm(x)*np.linalg.norm(y))#方法二:根据scipy库求解from scipy.spatial.distance import pdist X=np.vstack([x,y]) d2=1-pdist(X,'cosine')
两个向量完全相等时,余弦值为1,如下的代码计算出来的d=1。
d=1-pdist([x,x],'cosine')
8. 皮尔逊相关系数(Pearson correlation)
(1) 皮尔逊相关系数的定义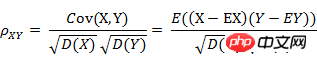
The cosine similarity mentioned earlier is only related to the direction of the vector, but it will be affected by the translation of the vector. In the angle cosine formula, if x is translated to x+ 1, the cosine value will change. How can translation invariance be achieved? This requires the use of Pearson correlation coefficient (Pearson correlation), sometimes also directly called Correlation coefficient.
If the cosine formula of the included angle is written as:
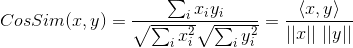
represents the cosine of the angle between vector x and vector y, then Pearson correlation coefficient can be expressed as:
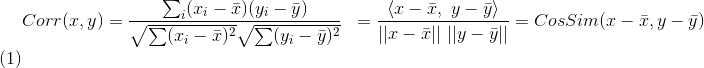
皮尔逊相关系数具有平移不变性和尺度不变性,计算出了两个向量(维度)的相关性。
在python中的实现:
import numpy as np x=np.random.random(10) y=np.random.random(10)#方法一:根据公式求解x_=x-np.mean(x) y_=y-np.mean(y) d1=np.dot(x_,y_)/(np.linalg.norm(x_)*np.linalg.norm(y_))#方法二:根据numpy库求解X=np.vstack([x,y]) d2=np.corrcoef(X)[0][1]
The correlation coefficient is a method of measuring the correlation between random variables X and Y. The value range of the correlation coefficient is [-1,1]. The larger the absolute value of the correlation coefficient, the higher the correlation between X and Y. When X and Y are linearly related, the correlation coefficient takes a value of 1 (positive linear correlation) or -1 (negative linear correlation).
9. Hamming distance (Hamming distance)
(1) The definition of Hamming distance
Two equal The Hamming distance between long strings s1 and s2 is defined as the minimum number of substitutions required to change one into the other. For example, the Hamming distance between the strings "1111" and "1001" is 2.
Application: Information coding (in order to enhance fault tolerance, the minimum Hamming distance between codes should be made as large as possible).
Implementation in python:
import numpy as npfrom scipy.spatial.distance import pdist x=np.random.random(10)>0.5y=np.random.random(10)>0.5x=np.asarray(x,np.int32) y=np.asarray(y,np.int32)#方法一:根据公式求解d1=np.mean(x!=y)#方法二:根据scipy库求解X=np.vstack([x,y]) d2=pdist(X,'hamming')
10. 杰卡德相似系数(Jaccard similarity coefficient)
(1) 杰卡德相似系数
两个集合A和B的交集元素在A,B的并集中所占的比例,称为两个集合的杰卡德相似系数,用符号J(A,B)表示。
杰卡德相似系数是衡量两个集合的相似度一种指标。
(2) 杰卡德距离
与杰卡德相似系数相反的概念是杰卡德距离(Jaccard distance)。杰卡德距离可用如下公式表示: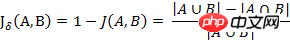
杰卡德距离用两个集合中不同元素占所有元素的比例来衡量两个集合的区分度。
(3) 杰卡德相似系数与杰卡德距离的应用
可将杰卡德相似系数用在衡量样本的相似度上。
样本A与样本B是两个n维向量,而且所有维度的取值都是0或1。例如:A(0111)和B(1011)。我们将样本看成是一个集合,1表示集合包含该元素,0表示集合不包含该元素。
在python中的实现:
import numpy as npfrom scipy.spatial.distance import pdist x=np.random.random(10)>0.5y=np.random.random(10)>0.5x=np.asarray(x,np.int32) y=np.asarray(y,np.int32)#方法一:根据公式求解up=np.double(np.bitwise_and((x != y),np.bitwise_or(x != 0, y != 0)).sum()) down=np.double(np.bitwise_or(x != 0, y != 0).sum()) d1=(up/down) #方法二:根据scipy库求解X=np.vstack([x,y]) d2=pdist(X,'jaccard')
11. 布雷柯蒂斯距离(Bray Curtis Distance)
Bray Curtis距离主要用于生态学和环境科学,计算坐标之间的距离。该距离取值在[0,1]之间。它也可以用来计算样本之间的差异。
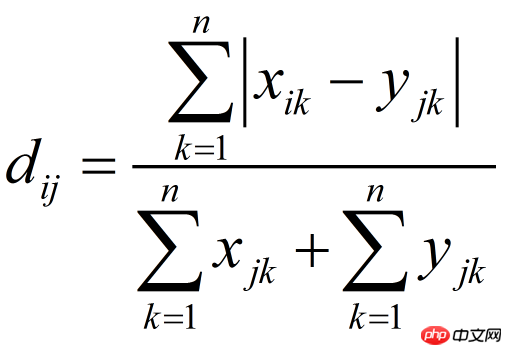
Sample data:
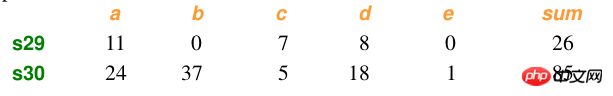
##Calculation:
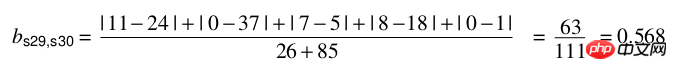
## Implementation in python:
import numpy as npfrom scipy.spatial.distance import pdist x=np.array([11,0,7,8,0]) y=np.array([24,37,5,18,1])#方法一:根据公式求解up=np.sum(np.abs(y-x)) down=np.sum(x)+np.sum(y) d1=(up/down) #方法二:根据scipy库求解X=np.vstack([x,y]) d2=pdist(X,'braycurtis')
相关推荐:
The above is the detailed content of Distance measurement and python implementation. For more information, please follow other related articles on the PHP Chinese website!




