
#著者| Wang Hao
##査読者| Chonglou21
世紀のインターネット技術といえば、Python/Rust/Go などに加え、その誕生一連の新しいプログラミング言語の登場や、情報検索技術の精力的な開発も見どころです。インターネットにおける最初の純粋なテクノロジーのビジネスモデルは、Google や Baidu に代表される検索エンジンテクノロジーでした。しかし、誰もが予想していないのは、推薦システムがずっと前に誕生したということです。 1992 という早い時期に、人類史上初の推薦システムが論文の形で発表されましたが、この時点では Google や Baidu はまだ誕生していませんでした。
必需品とされる検索エンジンとは異なり、すぐに多くのユニコーンが誕生しました。レコメンデーション システムをコア技術とするテクノロジー企業は、
—— 大規模言語モデルに基づく情報検索に遭遇しました。現在、先手は欧米諸国だが、現在は中国と米国が共同で進んでいる。 近年、レコメンデーション システムの分野で権威あるカンファレンス RecSys
は、頻繁に最優秀論文賞を# に授与しています。 ## シーケンスの推奨事項 #(連続的な推奨事項 #)。これは、この分野が垂直用途にますます注目していることを示しています。非常に重要なレコメンデーション システムの垂直用途がありますが、これまでのところ大きな波紋を起こしていません。この分野はシナリオベースのレコメンデーション (Context-aware Recommendation) であり、参照されています。 CARS として変換します。 CARS Workshop は時々見かけますが、これらの Workshop 論文はありません。年間 10 記事を超えると、やるべきことはあまりありません。 車 何に使えますか?まず、CARS
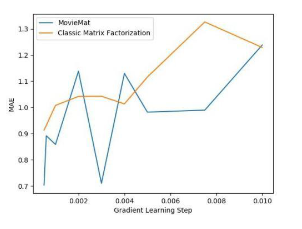
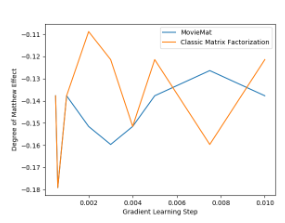
は、バーガーキングなどのファストフード企業ですでに使用されています。ユーザーが車を運転しているとき、シーンに応じてユーザーに音楽を推奨することもできます。さらに考えられるのは、気象状況に応じてユーザーに旅行プランを勧めることはできないだろうか?それともユーザーの体調に合わせて食事を勧めるのでしょうか?実際、想像力をフルに働かせれば、CARS のさまざまな実際的な応用例をいつでも見つけることができます。 しかし、CARS は非常に広く使用されているのに、なぜ論文を発表する人がこれほど少ないのかという疑問が生じます。理由は簡単です。CARS 利用可能な公開データセットがほとんどないからです。現在、CARS に最適な公開データセットは、スロベニアの LDOS-CoMoDa データセットです。これとは別に、他のデータセットを見つけるのは困難です。 LDOS-CoMoDa は、アンケート形式を使用して映画鑑賞時のシーン データをユーザーに提供しており、研究者の大多数が CARS に従事しています。研究が可能になる。このデータは 2012 から 2013 頃まで公開されていましたが、現在このデータ収集について知っている人はほとんどいません。 本題に戻りますが、この記事では主に MatMat / MovieMat アルゴリズムと PowerMat を紹介します。 アルゴリズム。これらのアルゴリズムは、CARS 問題を解決するための強力なツールです。まず、MatMat が CARS 問題をどのように定義するかを見てみましょう。まずユーザー評価マトリックスを再定義し、ユーザー評価を入れます。行列 各評価値を正方行列に置き換えます。正方行列の対角要素は元のスコア値であり、非対角要素はシーン情報です。 古典的な行列分解を変更する MatMat アルゴリズムの損失関数を以下に定義します。損失関数の形式は次のとおりです: どこで U および V はすべて行列です。このようにして、元の行列因数分解のベクトル内積を変更します。ベクトルのドット乗算を行列乗算に変換します。次の例を見てみましょう: MovieLens 小規模データセットでパフォーマンス テストを行ってみましょう 比較実験、次の結果が得られます。 MatMat アルゴリズムの方が優れていることがわかります。従来の行列因数分解アルゴリズムよりも優れています。レコメンデーション システムの公平性をもう一度確認してみましょう: MatMat は、公平性指標の点で依然として同等のパフォーマンスを発揮していることがわかります。 MatMat の解法プロセスは比較的複雑で、アルゴリズムを考案した著者ですら論文に導出過程を書いていません。しかし、よく言われるように、線形代数をしっかり学べば、世界中を旅することも怖くなくなります。賢明な読者であれば、関連する式を導き出し、このアルゴリズムを実装できると思います。 MatMat アルゴリズム ペーパーの元のアドレスは、次のリンクで見つけることができます: //m.sbmmt.com/ link/9b8c60725a0193e78368bf8b84c37fb2 。この論文は、国際学術会議 IEEE ICISCAE 2021 の最優秀論文レポート賞を受賞しました。 MatMat アルゴリズムは、シーンベースの映画推奨の分野に適用されます。このアルゴリズムの映画インスタンスの名前は、MovieMat です。 ###。 MovieMat の評価マトリックスは次のように定義されます: 作者は比較実験を行いました。 : LDOS-CoMoDa データ コレクション、MovieMat パフォーマンスは、従来の行列分解よりもはるかに高くなります。公平性の評価結果を見てみましょう: ##MovieMat ## の結果。 MovieMat のオリジナルの論文は、次のリンクでご覧いただけます: //m.sbmmt.com/link/f4ec6380c50a68a7c35d109bec48aebf 。 #このような問題に遭遇することがあります。新しい場所に到着し、シーン データのみがあり、ユーザー評価データがない場合はどうすればよいでしょうか?問題ではありません。Ratidar Technologies LLC ( Beijing Daping Qizhi Network Technology Co., Ltd.) は、## に基づいて発明されました。ゼロサンプル学習 #CARS アルゴリズム—— PowerMat。 PowerMat のオリジナルの論文は、次のリンクからご覧いただけます: //m.sbmmt.com/link/1514f187930072575629709336826443 。 PowerMat の発明者は、 および DotMat## から借用しました。 #、次の MAP 関数が定義されています: ここで、U はユーザー特徴ベクトル、V はユーザー特徴ベクトルです。 item feature Vector、R はユーザー評価値、C はシーン変数です。具体的には、次の式が得られます。 確率的勾配降下法を使用してこの問題を解決すると、次の式が得られます。 観察の結果、この数式セットには入力データに関連する変数がないことがわかりました。そのため、PowerMat はシナリオにのみ関連するゼロショット学習アルゴリズム。このアルゴリズムは次のシナリオに適用できます: 観光客は特定の場所への旅行を計画していますが、一度も行ったことがないため、天気やその他のシーン データしか持っていません。 # 観光客などにチェックインできるアトラクションを勧める#以下は、 と他のアルゴリズムとの比較データです: と MovieMat が均等に一致していることがわかりました。 # は ではなく、同等であり、結果は従来の行列分解アルゴリズムよりも優れています。以下の図は、公平性の観点から見ても、indicator、PowerMat が依然として強力なパフォーマンスを示していることを示しています: 比較実験を通じて、 CARS アルゴリズムであることがわかりました。 インターネット データ エンジニアは、データが何よりも重要であるとよく言います。そして 2010 の時代の頃、インターネットではデータに対して強気、アルゴリズムに対して弱気という強い傾向がありました。 CARS が良い例です。大多数の人が関連データにアクセスできないため、この分野の発展は大幅に制限されています。 LDOS-CoMoDa データコレクションを公開してくれたスロベニアの研究者のおかげで、私たちはこの分野を発展させる機会を得ました。また、より多くの人が CARS に注目し、CARS を実装し、 に貢献してくれることを願っています。車 資金調達…… Wang Hao、Funplus 人工知能研究所の元所長。彼は、ThoughtWorks、Douban、Baidu、Sina などの企業でテクノロジーおよびテクノロジーの幹部職を歴任してきました。インターネット企業、金融テクノロジー、ゲームなどの企業で #13 年間勤務し、人工知能、コンピューター グラフィックス、ブロックチェーンなどの分野で深い洞察力と豊富な経験を持っています。国際学会やジャーナルに 42 論文を発表し、IEEE SMI 2008 Best Paper Award、 ICBDT を受賞2020 / IEEE ICISCAE 2021 / AIBT 2023 / ICSIM 2024 最優秀論文レポート賞を受賞。 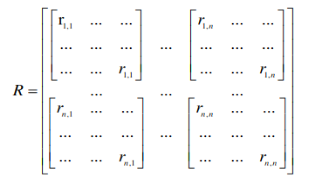
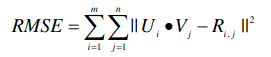

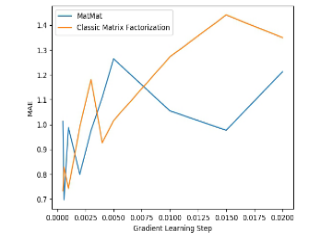
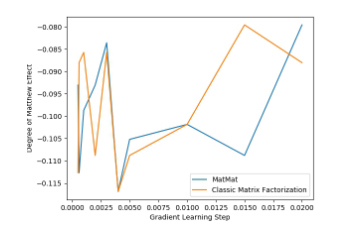
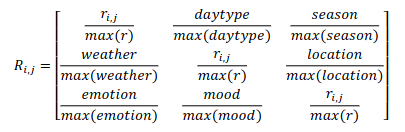
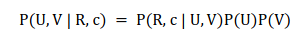
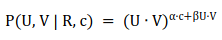
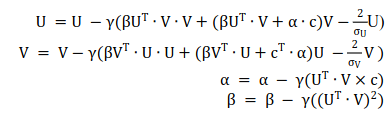
 PowerMat
PowerMat 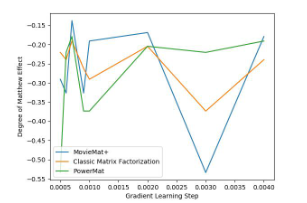 が優れた
が優れた
著者について
以上が線形代数をよく学び、推奨システムで遊びましょうの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。