機械学習の要点: 過学習を防ぐには?-AI-php.cn

実際、正則化の本質は非常に単純で、特定の目的を達成するために、特定の問題にアプリオリな制限や制約を課す手段や操作です。アルゴリズムで正則化を使用する目的は、モデルの過剰適合を防ぐことです。正則化というと、多くの学生はよく使われる L1 ノルムと L2 ノルムをすぐに思い浮かべるかもしれませんが、要約する前に、まず LP ノルムとは何かを見てみましょう。

LP ノルム

ノルムは、単純にベクトル空間の距離を表すものとして理解できますが、距離の定義は非常に抽象的です。 -否定的、再帰的、三角不等式、それは距離です。

LP ノルムはノルムではなく、次のように定義される一連のノルムです:

機械学習の要点: 過学習を防ぐには?

#p の範囲は [1, ∞) 。 p は、三角不等式に違反するため、(0,1) の範囲のノルムとして定義されません。

pp の変化に応じて、ノルムにもさまざまな変化が生じます。P ノルムの古典的な変化図を次のように借用します。 pが0から正の無限大まで変化するときの単位球の変化を示します。 P ノルムに基づいて定義された単位球は凸集合ですが、0

それでは、L0 ノルムとは何なのかという疑問が生じます。 L0 ノルムは、ベクトル内の非ゼロ要素の数を表し、次のように表されます:

機械学習の要点: 過学習を防ぐには?

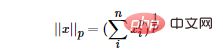
L0 ノルムを最小化することで、最も最適でないスパース特徴を見つけることができます。しかし残念なことに、L0 ノルムの最適化問題は NP 困難問題です (L0 ノルムも非凸です)。したがって、実際のアプリケーションでは、L0 の凸緩和を実行することがよくあります。L1 ノルムが L0 ノルムの最適な凸近似であることが理論的に証明されているため、通常は L0 ノルムを直接最適化する代わりに L1 ノルムが使用されます。

L1 ノルム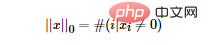

機械学習の要点: 過学習を防ぐには? LP ノルムの定義に従って、L1 ノルムの数学的形式を簡単に取得できます。

Pass As can上の式から分かるように、L1 ノルムはベクトルの各要素の絶対値の合計であり、「スパース正則化演算子」(Lasso 正則化) とも呼ばれます。そこで問題は、なぜスパース化が必要なのかということです。スパース化には多くの利点がありますが、最も直接的な利点は次の 2 つです。

機能選択機械学習の要点: 過学習を防ぐには?

解釈可能性

L2 ノルムは最もよく知られています。ユークリッド距離です。式は次のとおりです:

L2 ノルムには多くの名前があります。その回帰を「リッジ回帰」と呼ぶ人もいます。 " "（リッジ回帰）、これを「体重減少」と呼ぶ人もいます。 L2 ノルムを正則化項として使用すると、密な解を得ることができます。つまり、各特徴に対応するパラメーター ww が非常に小さく、0 に近いですが 0 ではありません。さらに、L2 ノルムを正則化項として使用すると、モデルが複雑すぎると過学習につながり、それによってモデルの汎化能力が向上します。

L1 ノルムと L2 ノルムの違い

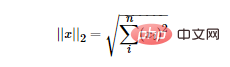機械学習の要点: 過学習を防ぐには? 次の図に示すように、L1 ノルムと L2 ノルムの違いを示す PRML の古典的な図を紹介します。

#上図に示すように、青い円は問題の可能な解の範囲を表し、オレンジ色の円は正規項の可能な解の範囲を表します。目的関数全体 (元の問題の正規項) には、2 つの解の範囲が接している場合に限り、解が存在します。上図から、L2 ノルムの解の範囲は円であるため、接点は座標軸上にない可能性が高く、L1 ノルムはひし形 (頂点が凸) であるため、その接点は座標軸上にないことが容易にわかります。接点は座標軸上にある可能性が高く、座標軸上の点は、１つの座標成分だけが非ゼロであり、他の座標成分はゼロである、つまり疎であるという特徴を有する。したがって、次の結論が得られます。L1 ノルムは疎な解をもたらす可能性があり、L2 ノルムは密な解をもたらす可能性があります。

ベイズ事前の観点から見ると、モデルをトレーニングするとき、現在のトレーニングデータセットのみに依存するだけでは十分ではありません。より優れた汎化機能を達成するには、多くの場合、事前項と正規項を追加する必要があります。先験的に追加することに相当します。

L1 ノルムはラプラス事前分布を追加することと同等です;
L2 ノルムは事前ガウス分布を追加することと同等です。

以下の図に示すように:

機械学習の要点: 過学習を防ぐには?

Dropout

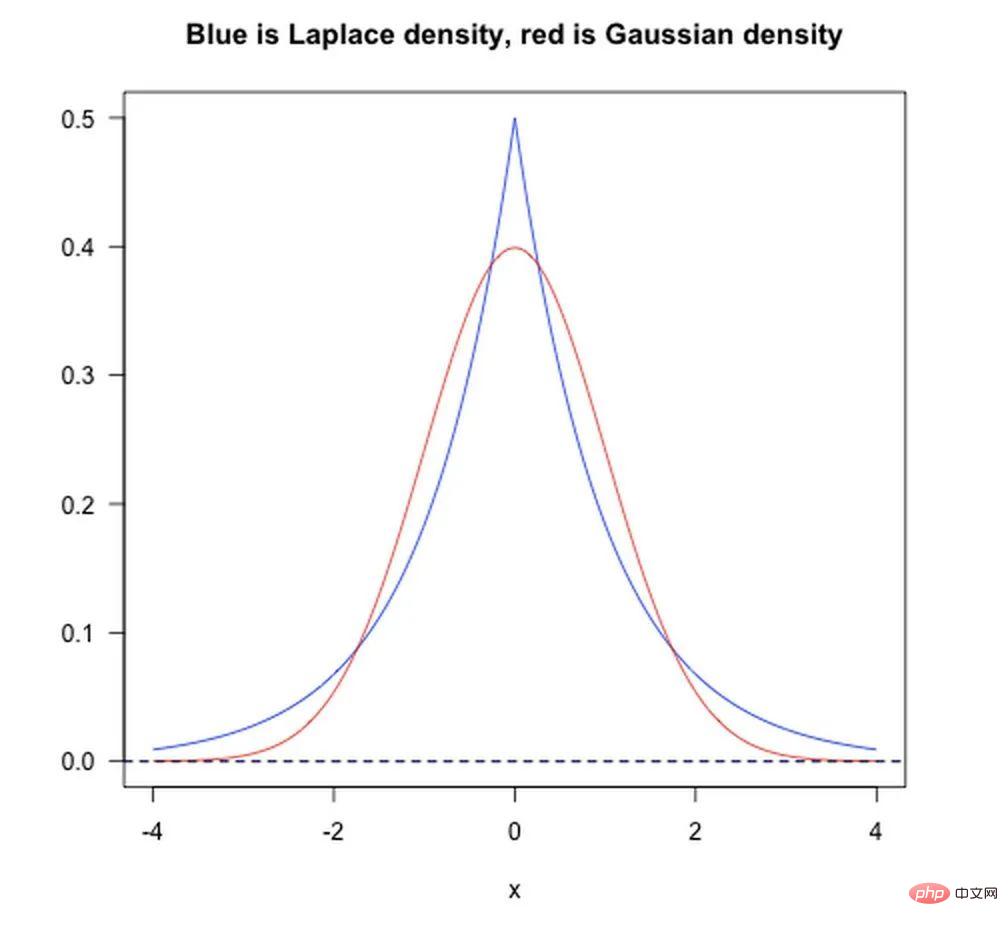
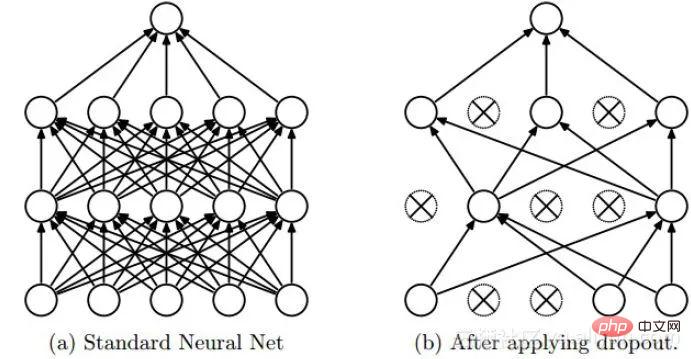
Dropout は深層学習でよく使用される正則化手法です。そのアプローチは、DNN のトレーニングプロセス中に確率 p で一部のニューロンを破棄する、つまり、破棄されたニューロンの出力が 0 であると単純に理解できます。 Dropout は、次の図に示すようにインスタンス化できます。

機械学習の要点: 過学習を防ぐには?

## Dropout の正則化効果は、次の 2 つの側面から直感的に理解できます。ドロップアウトトレーニングの各ラウンド中にニューロンをランダムに失うことは、複数の DNN を平均することと同等であるため、予測に使用すると投票の効果があります。

ニューロン間の複雑な同時適応を軽減します。隠れ層のニューロンがランダムに削除されると、完全に接続されたネットワークがある程度まで疎になり、異なる特徴の相乗効果が効果的に減少します。言い換えれば、一部の機能は固定関係を持つ隠れノードの共同作用に依存する可能性があり、ドロップアウトを通じて、一部の機能が他の機能が存在する場合にのみ有効である状況を効果的に組織化し、ニューラルネットワークの堅牢性を高めます。セックス。

バッチ正規化
バッチ正規化は厳密には正規化手法であり、主にネットワークの収束を加速するために使用されますが、ある程度の正則化効果もあります。

ここでは、Wei Xiushen 博士の Zhihu 回答における共変量シフトの説明への参照を示します。

注: 以下の内容は、Wei Xiushen 博士の Zhihu 回答から引用されています。統計的機械学習における古典的な前提が「ソース空間 (ソースドメイン) とターゲット空間 (ターゲットドメイン) のデータ分布」であることは誰もが知っています。「（配信は）一貫している」。それらが矛盾している場合、転移学習/ドメイン適応などの新しい機械学習の問題が発生します。共変量シフトは不一致分布を仮定した分岐問題であり、ソース空間とターゲット空間の条件付き確率は一致しているが、その周辺確率が異なることを意味します。よくよく考えてみると、確かにニューラルネットワークの各層の出力は、層内演算を経ているため、その分布が各層に対応する入力信号の分布とは明らかに異なっていることが分かります。ネットワークの深さが増すにつれて差は大きくなりますが、「示す」ことができるサンプルラベルは変化せず、共変量シフトの定義を満たします。

BN の基本的な考え方は、実際には非常に直観的です。なぜなら、非線形変換前のニューラルネットワークの活性化入力値 (X=WU B、U は入力) は、ネットワークの深さが深くなるにつれて、その値が大きくなるからです。分布は徐々にシフトまたは変化します (つまり、上記の共変量シフト)。トレーニングの収束が遅い理由は、一般に、全体の分布が非線形関数の値の範囲の上限と下限に徐々に近づくためです (シグモイド関数の場合、活性化入力値 X=WU B が大きな負または正であることを意味します)。 value) であるため、これによりバックプロパゲーション中に低レベルニューラルネットワークの勾配が消失します。これが、トレーニングにおけるディープニューラルネットワークの収束がますます遅くなる根本的な理由です。 BN は、特定の標準化手法を使用して、ニューラルネットワークの各層のニューロンの入力値の分布を、平均 0、分散 1 の標準正規分布に強制的に戻します。これにより、勾配分散の問題が発生します。アクティベーション機能。したがって、BN の役割は共変量シフトを軽減することであると言うよりも、BN が勾配分散問題を軽減できると言う方が適切です。

正規化、標準化、正則化

正規化については以前に説明しましたが、ここでは正規化と標準化について簡単に説明します。正規化: 正規化の目的は、元のデータを [a, b] 間隔にマッピングするための特定のマッピング関係を見つけることです。一般に、a と b は [−1,1]、[0,1] の組み合わせになります。通常、次の 2 つのアプリケーションシナリオがあります。

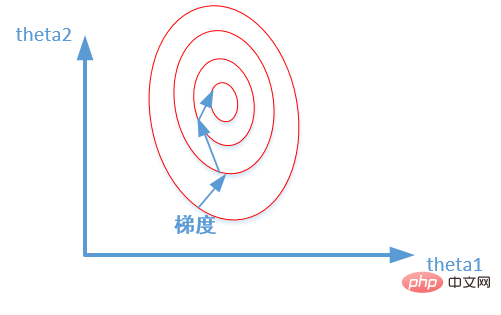
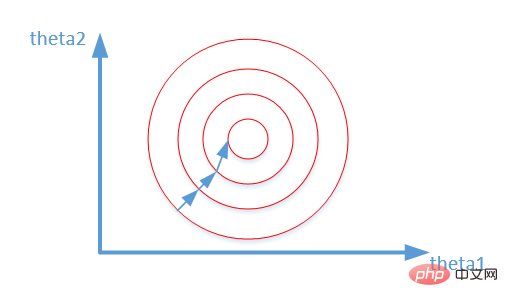
数値を (0, 1) の間の小数に変換します。

次元数値を無次元数値に変換します。