Quelle est l'aire d'un polygone régulier à n côtés d'un rayon donné ?

Ici, nous verrons comment calculer l'aire d'un polygone régulier à n côtés de rayon donné. Le rayon ici est la distance entre n'importe quel sommet et le centre. Pour résoudre ce problème, traçons une ligne verticale du centre vers l’un des côtés. Supposons que la longueur de chaque côté soit « a ». La perpendiculaire divise le côté en deux parties, chaque partie ayant une longueur a/2. Une ligne verticale et un rayon forment un angle x. Supposons que la longueur du rayon soit h.

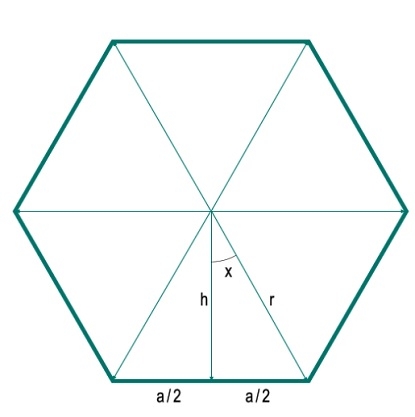
Ici, on voit que le polygone est divisé en N triangles égaux. Par conséquent, pour tout polygone ayant N côtés, il sera divisé en N triangles. L’angle au centre est donc de 360 degrés. Celui-ci est divisé en angles différents 360°/N (ici 360°/6 = 60°). L’angle x est donc de 180°/N. Nous pouvons maintenant facilement obtenir h et a en utilisant des équations trigonométriques.

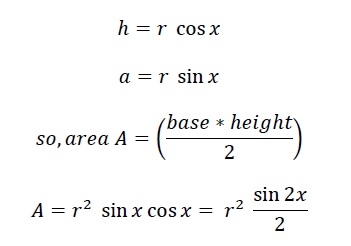
Maintenant, l'aire de l'ensemble du polygone est N*A.

Exemple

#include  #include  using namespace std; float polygonArea(float r, int n){ return ((r * r * n) * sin((360 / n) * 3.1415 / 180)) / 2; //convert angle to rad then calculate } int main() { float rad = 9.0f; int sides = 6; cout << "Polygon Area: " << polygonArea(rad, sides); }

Sortie

Polygon Area: 210.44

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!