
Avant d'introduire la transformation matricielle transform(), parlons de ce qu'est une matrice de transformation. 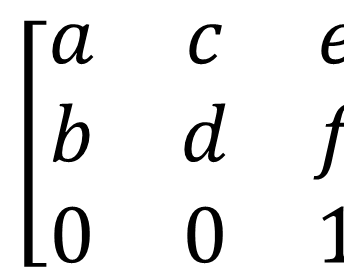
Ce qui précède est la matrice de transformation correspondant à la méthode transform() dans Canvas. Cette méthode transmet les six paramètres indiqués dans la figure, en particulier context.transform(a,b,c,d,e,f).
La signification de chaque paramètre correspond au tableau suivant :
| 参数 | 意义 |
|---|---|
| a | 水平缩放(1) |
| b | 水平倾斜(0) |
| c | 垂直倾斜(0) |
| d | 垂直缩放(1) |
| e | 水平位移(0) |
| f | 垂直位移(0) |
Lorsque nous remplaçons le 0 ou le 1 correspondant dans la matrice, nous pouvons constater qu'il s'agit d'une matrice d'identité (la valeur par défaut de la mise à l'échelle horizontale et verticale est 1, ce qui signifie une mise à l'échelle de 1 fois, c'est-à-dire aucune mise à l'échelle). Cette méthode utilise une nouvelle matrice de changement pour multiplier la matrice de transformation actuelle, puis obtient divers effets de changement.
Pour faire simple, lorsque l'on veut transformer un graphique, il suffit d'opérer les paramètres correspondants de la matrice de transformation. Après l'opération, multiplier les coordonnées de chaque point fixe du graphique par cette matrice pour obtenir une nouvelle. Les coordonnées du point fixe.
Méthode transform()
Le dessin sur toile nous fournit une méthode pour modifier cette matrice de transformation, c'est-à-dire transform().
Le système de coordonnées par défaut est basé sur le coin supérieur gauche du canevas comme origine des coordonnées (0, 0). Plus la valeur de l'axe X est située à droite, plus la valeur est grande, et plus la valeur de l'axe Y est située en bas, plus elle est grande. Dans le système de coordonnées par défaut, les coordonnées de chaque point sont directement mappées sur un pixel CSS. Certaines opérations spécifiques et paramètres de propriétés sur le canevas utilisent le système de coordonnées par défaut. Cependant, en plus du système de coordonnées par défaut, chaque canevas possède également une « matrice de transformation actuelle » dans le cadre de l'état graphique. Cette matrice définit le système de coordonnées actuel du canevas. Lorsque les coordonnées d'un point sont spécifiées, la plupart des opérations sur le canevas mappent le point sur le système de coordonnées actuel, plutôt que sur le système de coordonnées par défaut. La matrice de transformation actuelle est utilisée pour transformer les coordonnées spécifiées en coordonnées équivalentes dans le système de coordonnées par défaut. La transformation des coordonnées affecte également le dessin des segments de texte et de ligne.
L'appel de la méthode translate() déplace simplement l'origine des coordonnées vers le haut, le bas, la gauche et la droite. La méthode
rotate() fera pivoter l'axe des coordonnées dans le sens des aiguilles d'une montre selon l'angle spécifié.
La méthode scale() implémente l'extension et le raccourcissement de la distance sur l'axe des x ou l'axe des y. Passer une valeur négative permettra d'obtenir une
échelle pour inverser l'axe des coordonnées en utilisant l'origine des coordonnées comme point de référence. Comme un reflet dans un miroir.
translate est utilisé pour déplacer l'origine des coordonnées vers le coin inférieur gauche du canevas, puis la méthode d'échelle est utilisée pour inverser l'axe y, de sorte que l'axe y devienne plus grand à mesure qu'il monte.
Comprendre la transformation du système de coordonnées d'un point de vue mathématique :
Les méthodes de translation, de rotation et de mise à l'échelle sont faciles à comprendre si vous les imaginez comme des transformations des axes de coordonnées. Il est facile de comprendre la transformation de coordonnées d'un point de vue algébrique, c'est-à-dire d'imaginer la transformation comme un point (x, y) dans le système de coordonnées transformé, et le système de coordonnées d'origine devient (x`, y`).
Appelez c.translate(dx,dy). La méthode est équivalente à l'expression suivante
Il est recommandé d'utiliser transform() dans les situations suivantes :
1. Utilisez context.transform (1,0,0,1,dx,dy) au lieu de context.translate(dx,dy)
2. 0 ,0) au lieu de context.scale(sx, sy)
3. Utilisez context.transform(0,b,c,0,0,0) pour obtenir l'effet d'inclinaison (le plus pratique).
Il n'est pas nécessaire de l'utiliser pour réaliser la rotation. De plus, il n'est pas nécessaire de se souvenir de toutes ces conclusions. Notez simplement la signification des six paramètres de abcdef.
Regardons un code pour nous familiariser avec lui :
运行结果:
setTransform() signifie
transform() signifie que rotate(),scale(), translate() ou transform() sont utilisés. Il s'agit d'une fonction de transformation() qui permet de résoudre le problème.一点和之前的变换是一样的。
Vous pouvez utiliser setTransform() pour créer un contexte.
这里我们通过一个例子来说明:绘制一个矩形,通过 setTransform() 重置并创建新的变换矩阵,再次绘制矩形,重置并创建新的变换矩阵,然后再次绘制矩形。
运行结果:
解释一下过程:Le système setTransform() est également utilisé pour définir la fonction setTransform().下面的例子中,不会显示红色矩形,因为它在蓝色矩形下面。
 Quelles sont les méthodes de production de production d'animation html5 ?
Quelles sont les méthodes de production de production d'animation html5 ?
 La différence entre HTML et HTML5
La différence entre HTML et HTML5
 Comment résoudre le problème de l'écran noir après avoir allumé l'ordinateur et impossible d'accéder au bureau
Comment résoudre le problème de l'écran noir après avoir allumé l'ordinateur et impossible d'accéder au bureau
 l'explorateur Windows a cessé de fonctionner
l'explorateur Windows a cessé de fonctionner
 Comment résoudre l'échec de la résolution DNS
Comment résoudre l'échec de la résolution DNS
 Les principaux composants qui composent le CPU
Les principaux composants qui composent le CPU
 geforce 940mx
geforce 940mx
 solution de panique du noyau
solution de panique du noyau