Application des graphiques : chemin le plus court
Avez-vous l'impression d'avoir encore plus à apprendre sur l'arbre couvrant minimum dans l'article précédent ? Je ne sais pas dans quelle mesure tout le monde l'a maîtrisé. Avez-vous compris les principes de Prim et Kruskal ? Si vous ne pouvez pas l'écrire pendant l'entretien, donnez au moins une idée générale. Bien sûr, si vous êtes un étudiant qui passe l'examen d'entrée de troisième cycle, vous devez comprendre et mémoriser en profondeur le code de l'ensemble de l'algorithme.
Quel est le chemin le plus court
Aujourd'hui, nous apprenons un autre problème classique dans les applications graphiques, qui est le problème du chemin le plus court. Ce problème est différent de l'arbre couvrant minimum. L'exigence de l'arbre couvrant minimum est de connecter tous les nœuds et de prendre l'itinéraire avec le plus petit poids. Le chemin le plus court fait référence au chemin ayant le plus petit poids d’un sommet à un autre sommet. Ce chemin n'est pas nécessairement inclus dans l'arbre couvrant minimum, ils ne sont donc pas très liés.
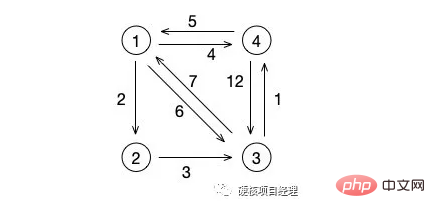
D'après cette image, notre chemin le plus court du nœud 1 au nœud 2 est 2, c'est évident. Alors qu’en est-il du nœud 1 au nœud 3 ? Pas le chemin du milieu direct avec un poids de 6, mais le chemin 1->2->3, qui est le chemin avec un poids total de 5.
Ensuite, regardons le nœud 3. Le chemin le plus court entre celui-ci et le nœud 1 devrait être le chemin 3->4->1, c'est-à-dire le chemin avec un poids de 6, pas celui du milieu. Un chemin droit. avec un poids de 7.
Oui, c'est le concept du chemin le plus court. Par le chemin le plus court, nous résolvons généralement le problème du graphe unidirectionnel, mais qu'en est-il dans la vraie vie ? Les applications cartographiques les plus courantes sont en fait les graphiques bidirectionnels. Cependant, cela n'affecte pas notre apprentissage. Nous pouvons considérer les nœuds de cet exemple de diagramme comme des gares urbaines. Même les lignes de train reliant le nœud 1 et le nœud 3 n'allent pas nécessairement en même temps. Par exemple, la durée totale du trajet du train Z2 de Changsha à Pékin est de 14 heures et 42 minutes, tandis que le temps de retour du train Z1 est de 14 heures et 10 minutes. Pouvons-nous donc choisir d'autres trains ? Par exemple, un train peut prendre seulement 8 heures de Changsha à Shijiazhuang, puis seulement 2 heures de Shijiazhuang à Pékin. De cette façon, le temps total que nous choisirons cet itinéraire ne prendra que 10 heures (sur 10 heures). bien sûr, ce n'est qu'un exemple. Les gens choisiront certainement le train à la gare de départ s'il ne s'agit pas d'un train à grande vitesse.)
Algorithme Floyd du chemin le plus court multi-sources
Tout d'abord, parlons d'un algorithme de chemin le plus court multi-sources. Alors, qu’est-ce que le multi-source ?
En fait, cet algorithme peut trouver le chemin le plus court de tous les nœuds à tous les nœuds. C'est vrai, avec cet algorithme, quel que soit le nœud qui va à quel nœud, le chemin le plus court entre eux est calculé en même temps. Est-ce magique ? Non, non, non, ce qui est encore plus étonnant, et ce qui vous fera crier Oh mon Dieu dans un instant, c'est son code de base, qui ne fait que cinq lignes ! !
function Floyd($graphArr){
$n = count($graphArr);
for($k = 1;$k<=$n;$k++){ // 设 k 为经过的结点
for($i = 1;$i<=$n;$i++){
for($j = 1;$j<=$n;$j++){
// 如果经过 k 结点 能使 i 到 j 的路径变短，那么将 i 到 j 之间的更新为通过 k 中转之后的结果
if($graphArr[$i][$j] > $graphArr[$i][$k] + $graphArr[$k][$j]){
$graphArr[$i][$j] = $graphArr[$i][$k] + $graphArr[$k][$j];
}
}
}
}
for($i = 1;$i<=$n;$i++){
for($j = 1;$j<=$n;$j++){
echo $graphArr[$i][$j], ' ';
}
echo PHP_EOL;
}
}
// 请输入结点数：4
// 请输入边数：8
// 请输入边，格式为 出 入 权：1 2 2
// 请输入边，格式为 出 入 权：1 3 6
// 请输入边，格式为 出 入 权：1 4 4
// 请输入边，格式为 出 入 权：2 3 3
// 请输入边，格式为 出 入 权：3 1 7
// 请输入边，格式为 出 入 权：3 4 1
// 请输入边，格式为 出 入 权：4 1 5
// 请输入边，格式为 出 入 权：4 3 12
// 0 2 5 4
// 9 0 3 4
// 6 8 0 1
// 5 7 10 0Nous pouvons d'abord vérifier le résultat, qui est la sortie matricielle à la fin du commentaire. Les distances les plus courtes entre le nœud 1 et les nœuds 2, 3 et 4 sont 2, 5 et 4. La distance la plus courte entre le nœud 3 et les nœuds 1, 2 et 4 est 6, 8 et 1. En d’autres termes, la matrice de contiguïté du graphe original devient la matrice du chemin le plus court. Chaque ligne représente la distance la plus courte entre chaque nœud et les autres nœuds.
D'accord, le résultat est bon, alors quel est exactement le code écrit ? C'est quoi ce k ? Ne vous inquiétez pas, regardons les choses étape par étape.
En supposant que la distance entre les deux points n'est pas la plus courte, alors il doit y avoir un autre point comme support pour sauter Du point i, sautez d'abord vers ce point puis sautez vers le point j. Un tel chemin est plus direct Si. i est proche de j, nous définissons ce point comme k point
Mais nous ne savons pas à quel nœud aller, et il peut y avoir plus d'un k. Peut-être devons-nous passer par plusieurs k de i à j. temps, nous commençons à parcourir à partir de k, qui est le premier niveau de boucle
Sous le premier niveau de boucle, nous effectuons notre boucle de parcours normale de i et j, et obtenons la longueur de i directement à j, qui est [i] [j ]. À l’heure actuelle, en raison de l’existence du k le plus à l’extérieur, nous connaissons également la longueur de k à j si je marche à partir de k, qui est la distance [i][k] + [k][i]
Évidemment, si la distance de [i][k] + [k][i] est plus courte que [i][j], la valeur de [i][j] est mise à jour à [i][k] + [k] [i ]
Une fois les boucles internes i et j terminées, le parcours du premier nœud en tant que saut multimédia est également terminé. Les poids entre chaque nœud de la matrice actuelle ont été traités via le premier nœud. moyen
Cependant, ce n'est pas exact. Peut-être que le chemin que nous pouvons parcourir par i, k1, k2, j est le plus court, donc la boucle k externe continue de traverser et les deuxièmes nœuds servent de nœuds intermédiaires
et le cycle. continue jusqu'à ce que tous les nœuds aient traversé une fois les nœuds intermédiaires intermédiaires, et nous obtenons un graphique matriciel du chemin le plus court, qui est le résultat de notre code de test ci-dessus
Prenons le nœud 4 et le nœud 3 sera expliqué. Nous définissons 4 comme i et le nœud 3 comme j.
初始化时，[i][j] 为 12 ，这个没什么问题，单向图的那条带箭头的边的权值就是 12 。
然后当 k 为 1 时，也就是我们经过结点 1 来看路径有没有变短，这时 [i][k] 是 5 ，[k][j] 是 6 ，OK，路径变成 11 了，把 [i][j] 的值改成 11 。
同时，在 i 为 4 ，j 为 2 的情况下，他们两个的最短路径也在这次 k=1 的循环中被赋值为 7 。最开始 4 到 2 是没有直接的边的，现在在结点 1 的连接下，他们有了路径，也就是 [4][2] = [4][1] + [1][2] = 7 。
当 k 为 2 时，[i][j] 为 11 ，这时 [i][k] 就是上面说过的 [4][2] 。也就是 7 ，而 [k][j] 则是 3 ，路径又缩小了，[i][k] + [k][j] = 10 ，[i][j] 现在又变成了 10 。
循环继续，但已经没有比这条路径更小的值了，所以最后 [4][2] 的最短路径就是 10 。
看着晕吗？拿出笔来在纸上或者本子上自己画画，每一步的 k 都去画一下当前的最短路径矩阵变成什么样了。这样画一次之后，马上就知道这个 Floyd 算法的核心奥秘所在了。
不得不说，前人的智慧真的很伟大吧，不过说是前人，其实 Floyd 大佬在 1962 年才发表了这个算法，但这个算法的核心思想却是数学中的动态规划的思想。所以说，算法和数学是没法分家的，各位大佬哪个不是数学界的一把手呢。
单源最短路径 Dijkstra 算法
说完了多源最短路径，我们再讲一个鼎鼎大名的单源最短路径的算法。虽说上面的多源很牛X，但是它的时间复杂度也就是时间效率也确实是太差了，没看错的话三个 N 次的循环嵌套就是 O(N3)。如果数据稍微多一点的话基本就可以从 Oh!My God! 变成 Oh!FxxK! 了。而且大多数情况下，我们的需求都会是固定的求从某一点到另一点的最短路径问题，也就是单源最短路径问题。这时，就可以使用这种效率稍微好一点的算法来快速地解决了。
// origin 表示源点，也就是我们要看哪个结点到其它结点的最短路径
function Dijkstra($graphArr, $origin)
{
$n = count($graphArr);
$dis = []; // 记录最小值
$book = []; // 记录结点是否访问过
// 初始化源点到每个点的权值
for ($i = 1; $i <= $n; $i++) {
$dis[$i] = $graphArr[$origin][$i]; // 源点到其它点的默认权值
$book[$i] = 0; // 所有结点都没访问过
}
$book[$origin] = 1; // 源点自身标记为已访问
// 核心算法
for ($i = 1; $i <= $n - 1; $i++) {
$min = INFINITY;
// 找到离目标结点最近的结点
for ($j = 1; $j <= $n; $j++) {
// 如果结点没有被访问过，并且当前结点的权值小于 min 值
if ($book[$j] == 0 && $dis[$j] < $min) {
$min = $dis[$j]; // min 修改为当前这个节点的路径值
$u = $j; // 变量 u 变为当前这个结点
}
// 遍历完所有结点，u 就是最近的那个顶点
}
$book[$u] = 1; // 标记 u 为已访问
for ($v = 1; $v <= $n; $v++) {
// 如果 [u][v] 顶点小于无穷
if ($graphArr[$u][$v] < INFINITY) {
// 如果当前 dis[v] 中的权值大于 dis[u]+g[u][v]
if ($dis[$v] > $dis[$u] + $graphArr[$u][$v]) {
// 将当前的 dis[v] 赋值为 dis[u]+g[u][v]
$dis[$v] = $dis[$u] + $graphArr[$u][$v];
}
}
}
// 最近的结点完成，继续下一个最近的结点
}
for ($i = 1; $i <= $n; $i++) {
echo $dis[$i], PHP_EOL;
}
}
// 请输入结点数：4
// 请输入边数：8
// 请输入边，格式为 出 入 权：1 2 2
// 请输入边，格式为 出 入 权：1 3 6
// 请输入边，格式为 出 入 权：1 4 4
// 请输入边，格式为 出 入 权：2 3 3
// 请输入边，格式为 出 入 权：3 1 7
// 请输入边，格式为 出 入 权：3 4 1
// 请输入边，格式为 出 入 权：4 1 5
// 请输入边，格式为 出 入 权：4 3 12
// 测试第四个结点到其它结点的最短路径
Dijkstra($graphArr, 4);
// 5
// 7
// 10
// 0代码一下增加了不少吧，不过仔细看一下核心的算法部分，这次只是两层循环的嵌套了，时间复杂度一下子就降到了 O(N2) ，这一下就比 Floyd 算法提升了很多。当然，它的场景也是有限的，那就是只能一个结点一个结点的计算。
好了，我们还是来看一下 Dijkstra 到底在干嘛吧。我们依然是使用上面那个简单的图，并且还是研究结点 4 到其它结点的算法执行情况。
首先，我们初始化结点 4 到其他所有结点的默认值，这时结点 4 到结点 2 是没有直接路径的，所以是无穷大，而到结点 1 是 5，到结点 3 是 12 。
然后将结点 4 标记为已访问，也就是 book[4] = 1
进入核心算法，从头开始遍历结点，这里是标记为 i 下标，因为这里是单源的最短路径，所以我们不需要再看自己到自己的最短路径了，只需要 n-1 次循环就可以了
开始 j 层的循环，先判断当前的结点是否已经被标记过，没有被标记过的话再看它的值是否是最小的，最后循环完成后获得一个从结点 4 出发的权值最小的路径，并将这条路径到达的结点下标记为 u ，标记 u 下标的这个结点为已访问结点
进入 v 循环，判断图中 u 到 v 的结点是否是无穷，如果不是的话再判断 u 到 v 的结点加上原来的 dis[u] 的权值是否小于 dis[v] 中记录的权值，如果比这个小的话，更新 dis[v] 为 u 到 v 的结点加上原来的 dis[u] 的权值
循环重复地进行比较完成算法
对于结点 4 来说，dis 经历了如下的变化：
首先，默认情况下 dis = [5, 9999999, 12, 0]
第一次循环后，结点1 完成查找，并在 v 的循环中发现了可以从结点1 到结点2 和结点3 而且比原来的值都要小 ，于是 dis = [5, 7, 11, 0]
第二次循环后，结点2 完成查找，这次循环发现从结点2 到结点3 的距离更短，于是 dis = [5, 7, 10, 0]
第三次循环后，结点3 完成查找，没有发现更短的路径，dis = [5, 7, 10, 0]
看明白了吗？不明白的话自己试试吧，不管是断点还是在中间输出一下 dis 和 book ，都能够帮助我们更好地理解这个算法的每一步是如何执行的。从代码中就可以看出来，这个 Dijkstra 算法的时间复杂度是 O(N2) ，这可比 Floyd 快了不少了吧。
总结
关于图的两种最典型的应用及算法就到这里结束了。当然，图的内容可远不止这些，比较典型的还是进度网络图等的算法，特别是做一些项目管理类的系统时会非常有用。当然，更高深的内容就要去研究《图论》了。这个可就远超我的水平了，希望有更多数学相关基础的同学能够继续深入研究。而我嘛，先去恶补下数学吧！！
测试代码： https://github.com/zhangyue0503/Data-structure-and-algorithm/blob/master/5.图/source/5.5图的应用：最短路径.php
推荐：《PHP视频教程》
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Comment ouvrir le fichier php
Comment supprimer les premiers éléments d'un tableau en php
Que faire si la désérialisation php échoue
Comment connecter PHP à la base de données mssql
Comment connecter PHP à la base de données mssql
Comment télécharger du HTML
Comment résoudre les caractères tronqués en PHP
Comment ouvrir des fichiers php sur un téléphone mobile
![[Web front-end] Démarrage rapide de Node.js](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
