N algorithmes pour la séquence de Fibonacci en PHP

Préface

Il y a quelque temps, j'ai rencontré la méthode récursive conventionnelle d'optimisation du calcul de la séquence de Fibonacci, mais une fois que Time n'a pas trouvé une bonne méthode à temps, j'ai donc recherché des informations pertinentes plus tard et résumé une variété de solutions de calcul, je les ai donc partagées avec tout le monde pour communiquer et apprendre ensemble.

Recommandé : "Tutoriel vidéo PHP"

Que sont les nombres de Fibonacci

Fibonacci La séquence de Fibonacci, également connue sous le nom de séquence du nombre d'or, a été introduite par le mathématicien Leonardoda Fibonacci en utilisant l'élevage de lapins comme exemple, elle est donc également appelée « séquence du lapin ». Elle fait référence à cette séquence de nombres : 1, 1, 2, 3, 5. , 8, 13, 21, 34,... Mathématiquement, la suite de Fibonacci est définie récursivement comme suit : F(1)=1, F (2)=1, F(n)=F(n - 1)+F (n - 2) (n ≥ 3, n ∈ N*).

Maintenant que nous savons 斐波那契数, utilisons différentes méthodes pour calculer et obtenir le Nième nombre de Fibonacci.

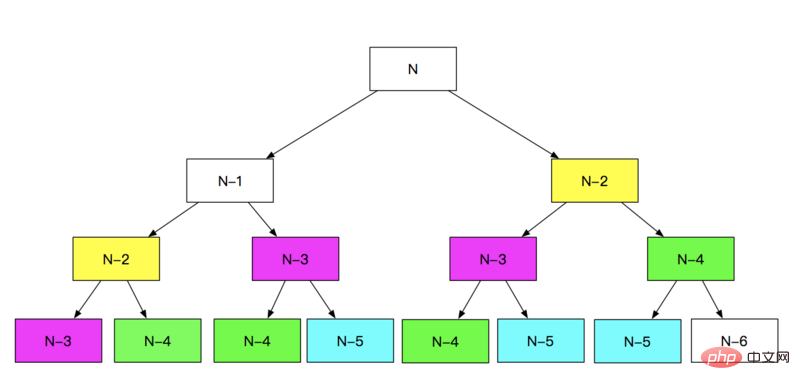
Récursivité ordinaire

Cette méthode est la plus conventionnelle. Elle peut être calculée directement selon la définition de F(n)=F(n - 1)+F(n - 2) récursivité, mais les performances sont les plus faibles.

/**
 * 普通递归
 * @param int $n
 * @return int
 */function fib($n = 1){    // 低位处理
    if ($n < 3) {        return 1;
    }    // 递归计算前两位
    return fib($n - 1) + fib($n - 2);
}

Optimisation récursive

Comme vous pouvez le voir grâce à la méthode récursive ci-dessus, de nombreux calculs répétés sont effectués et les performances sont extrêmement mauvaises si N est plus grand. , le nombre de calculs sera trop important. C'est terrible. Eh bien, puisque les calculs répétés affectent les performances, l'optimisation commence par réduire les calculs répétés, c'est-à-dire stocker les données précédemment calculées, évitant ainsi trop de calculs répétés et optimisant l'algorithme récursif.

/**
 * 递归优化
 * @param int $n
 * @param int $a
 * @param int $b
 * @return int
 */function fib_2($n = 1, $a = 1, $b = 1){    if ($n > 2) {        // 存储前一位，优化递归计算
        return fib_2($n - 1, $a + $b, $a);
    }    return $a;
}

Mémoire ascendante

De bas en haut calcule de manière itérative le sous-problème des nombres de Fibonacci et stocke la valeur calculée, en passant la valeur calculée. Effectuez des calculs. Utilisez les boucles for pour réduire le problème des calculs répétés causés par la récursion.

/**
 * 记忆化自底向上
 * @param int $n
 * @return int
 */function fib_3($n = 1){
    $list = [];    for ($i = 0; $i <= $n; $i++) {        // 从低到高位数，依次存入数组中
        if ($i < 2) {
            $list[] = $i;
        } else {
            $list[] = $list[$i - 1] + $list[$i - 2];
        }
    }    // 返回最后一个数，即第N个数
    return $list[$n];
}

Itérer de bas en haut

Le bit le plus bas est initialisé et attribué, et utilisez for pour calculer de manière itérative de bas en haut pour obtenir le Nième nombre.

/**
 * 自底向上进行迭代
 * @param int $n
 * @return int
 */function fib_4($n = 1){    // 低位处理
    if ($n <= 0) {        return 0;
    }    if ($n < 3) {        return 1;
    }
    $a = 0;
    $b = 1;    // 循环计算
    for ($i = 2; $i < $n; $i++) {
        $b = $a + $b;
        $a = $b - $a;
    }    return $b;
}

Méthode de formule

En comprenant la relation entre la séquence de Fibonacci et le nombre d'or, utilisez le nombre d'or pour calculer le Nème numéro d'acte de Fibonacci.

/**
 * 公式法
 * @param int $n
 * @return int
 */function fib_5($n = 1){    // 黄金分割比
    $radio = (1 + sqrt(5)) / 2;    // 斐波那契序列和黄金分割比之间的关系计算
    $num = intval(round(pow($radio, $n) / sqrt(5)));    return $num;
}

La méthode invincible et imbattable

Je n'entrerai pas dans les détails de cette méthode. Tout le monde la connaît, mais ne l'essayez pas facilement...<. 🎜>

/**
 * 无敌欠揍法
 * @param int $n
 * @return int
 */function fib_6($n = 1){    // 列举了30个数
    $list = [1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269];    return $list[$n];
}

Copier après la connexion

Enfin

D'accord, je viens d'écrire plusieurs solutions. S'il y a quelque chose qui ne va pas, s'il vous plaît. signalez-le et je le réviserai à temps. Si vous avez d'autres méthodes de calcul, n'hésitez pas à les partager pour communiquer et apprendre ensemble. Merci !

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!