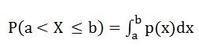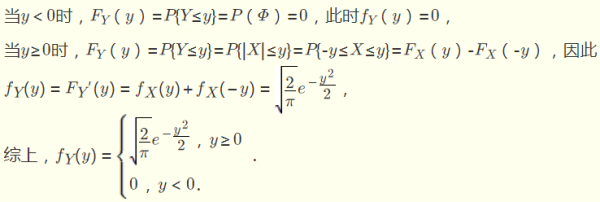A simple explanation of the probability density function

Can you briefly explain what the probability density function is?

The probability density function (p.d.f., probability density function) describes the probability distribution of random variables and is the derivative function of the cumulative distribution function. [Edit] Definition For a one-dimensional real random variable X, any function $f\_X\; (x)$ that satisfies the following conditions can be defined as its probability density function: $f\_\; (x)\backslash ge\; 0,\; -\backslash infty$ \backslash int\_\{-\backslash infty\}^\{\backslash infty\}\; f\_\; (x)\backslash ,dx\; =\; 1$The\; probability\; of\; random\; variable\; X\; in\; the\; interval\; can\; be\; determined\; by\; its\; probability\; The\; definite\; integral\; representation\; of\; the\; density\; function:$ P[a\; and$ F(x)=P[Xis\; the\; cumulative\; distribution\; function\; of\; X.\; Obviously\; the\; probability\; density\; function\; is\; its\; derivative\; function.\; [Edit]Application\; Moments\; such\; as\; expected\; value\; and\; variation\; can\; be\; obtained\; from\; the\; probability\; density\; function.\; Expected\; value\; (first\; moment):\; E[X]=$ \backslash int\_\{-\backslash infty\}^\{\backslash infty\}\; xf(x)\backslash ,dx$Variation\; (second\; moment):\; VAR[X]=$ \backslash int\_\{-\backslash infty\}^\{\backslash infty\}\; (x-E[X])^2f(x)\backslash ,dx$[edit]\; Characteristic\; function\; can\; be\; obtained\; by\; Fourier\; transformation\; of\; the\; probability\; density\; function.$ \backslash Phi\_X(j\backslash omega)\; =\; \backslash int\_\{-\backslash infty\}^\{\backslash infty\}\; f(x)e^\{j\backslash omega\; x\}\backslash ,dx$There\; is\; a\; one-to-one\; relationship\; between\; the\; characteristic\; function\; and\; the\; probability\; density\; function\; Relationship.\; Therefore,\; knowing\; the\; characteristic\; function\; of\; a\; distribution\; is\; equivalent\; to\; knowing\; the\; probability\; density\; function\; of\; a\; distribution.\; da:Sandsynlighedst\ae thedsfunktion\; en:Probability\; density\; function\; it:Funzione\; di\; densità\; di\; probabilità\; nl:Kansdichtheid\; sv:Täthetsfunktion$$$

A beam of particles is dispersed by an obstacle (located at x = 0). Its wave function is as follows:

Ψ（x, t） = Ae-iEt/h[when x

Ψ（x, t） = e-iEt/h( Beikx Ce-ikx) [when x> 0 ]

Where E = h2k2/( 2m ) and k > 0, A, B and C are complex coefficients.

﹝The "h" is "h-bar", which is the horizontal line above h﹞

(a) Calculate its probability density p(x, t) when x

(b) Calculate its probability flow density j(x, t) when x

(c) Calculate its probability density p(x, t) when x > 0.

(d) Calculate its probability flow density j(x, t) when x > 0.

(e) The wave function above contains three different parts, three coefficients A, B and C. Tell whether each one moves right or left. The three of them represent incidence, reflection and emission respectively. Which one is that?

Note: The answers to p(x, t) and j(x, t) must be real numbers.

How to distinguish between probability function and probability density

Mathematical definition of probability density

For random variable X, if there is a non-negative integrable function p(x) (﹣∞

Continuous random variables are often intuitively described by their probability density functions. The probability density function f(x) of continuous random variables has the following properties:

This refers to one-dimensional continuous random variables, and multi-dimensional continuous variables are similar.

Probability density function of random data: represents the probability that the instantaneous amplitude falls within a specified range, so it is a function of amplitude. It varies with the magnitude of the range taken.

The density function f(x) has the following properties:

(1)f(x)≧0;

(2) ∫f(x)d(x)=1;

(3) P(a

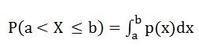
Suppose the probability density function of random variable X N0 1 Y |x| Y

The problem-solving process is as follows:

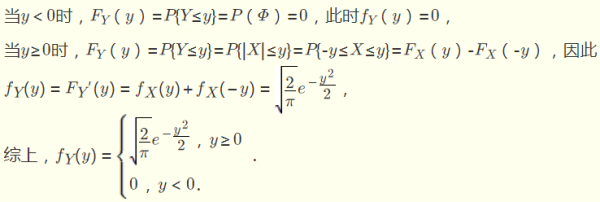
Extended information

Probability density method:

Suppose the random variable Among them, α=min(g(-∞), g(∞)), β=max(g(-∞), g(∞)), h(y) is the inverse function of g(x). Simply talking about probability density has no practical significance. It must have a certain bounded interval as a premise. The probability density can be regarded as the ordinate and the interval as the abscissa. The integral of the probability density over the interval is the area, and this area is the probability of an event occurring in this interval. The sum of all areas is 1. Therefore, it is meaningless to analyze the probability density of a point alone. It must have an interval as a reference and comparison.

Probability refers to the probability of an event occurring randomly. For a uniform distribution function, the probability density is equal to the probability of an interval (the value range of the event) divided by the length of the interval. Its value is non-negative and can be very large. Very small.

Select one product at random from a batch of genuine and defective products. "The one you draw is genuine" is a random event. Suppose a random phenomenon is tested and observed n times, and event A occurs m times, that is, its frequency of occurrence is m/n. After a lot of repeated experiments, m/n often gets closer and closer to a certain constant (see Bernoulli's law of large numbers for proof of this conclusion).

The above is the detailed content of A simple explanation of the probability density function. For more information, please follow other related articles on the PHP Chinese website!