Through MAmmoT, LLM becomes a mathematical generalist: from formal logic to four arithmetic operations

Mathematical reasoning is an important capability of modern large language models (LLM). Despite some recent progress in this field, there is still a clear gap between closed source and open source LLM. Closed-source models such as GPT-4, PaLM-2, and Claude 2 dominate common mathematical reasoning benchmarks such as GSM8K and MATH, while open-source models such as Llama, Falcon, and OPT lag significantly behind on all benchmarks

In order to solve this problem, the research community is working hard in two directions

(1) Continuous pre-training methods such as Galactica and MINERVA can perform training on more than 100 billion The LLM is continuously trained on the basis of mathematically related network data. This method can improve the general scientific reasoning ability of the model, but the computational cost is higher

Rejection sampling fine-tuning (RFT) and specific data set fine-tuning methods such as WizardMath, that is, using the specific data set Supervise data to fine-tune the LLM. While these methods can improve performance within a specific domain, they do not generalize to broader mathematical reasoning tasks beyond fine-tuning data. For example, RFT and WizardMath can improve the accuracy by more than 30% on GSM8K (one of which is a fine-tuned dataset), but hurt the accuracy on datasets outside the domain such as MMLU-Math and AQuA, making it lower As much as 10%

Recently, a research team from the University of Waterloo, Ohio State University and other institutions proposed a lightweight but generalizable mathematical instruction fine-tuning method that can be used Enhance the general (i.e. not limited to fine-tuning tasks) mathematical reasoning capabilities of LLM.

Rewritten content: In the past, the method of focus was mainly the chain of thought (CoT) method, which is to solve mathematical problems through step-by-step natural language description. This method is very general and can be applied to most mathematical disciplines, but has some difficulties with computational accuracy and complex mathematical or algorithmic reasoning processes (such as solving roots of quadratic equations and calculating matrix eigenvalues)

In contrast, code format prompt design methods such as Program of Thought (PoT) and PAL use external tools (i.e., Python interpreters) to greatly simplify the mathematical solution process. This approach is to offload the computational process to an external Python interpreter to solve complex mathematical and algorithmic reasoning (such as solving quadratic equations using sympy or computing matrix eigenvalues using numpy). However, PoT struggles with more abstract reasoning scenarios, such as common sense reasoning, formal logic, and abstract algebra, especially without a built-in API.

In order to take into account the advantages of both CoT and PoT methods, the team introduced a new mathematical hybrid instruction fine-tuning data set, MathInstruct, which has two main features: (1) Broadly covers different mathematical fields and levels of complexity, (2) blending CoT and PoT principles

MathInstruct Based on seven existing mathematical principle data sets and six newly compiled of data sets. They used MathInstruct to fine-tune Llama models of different sizes (from 7B to 70B). They called the resulting model the MAmmoTH model, and found that MAmmoTH had unprecedented capabilities, like a mathematical generalist.

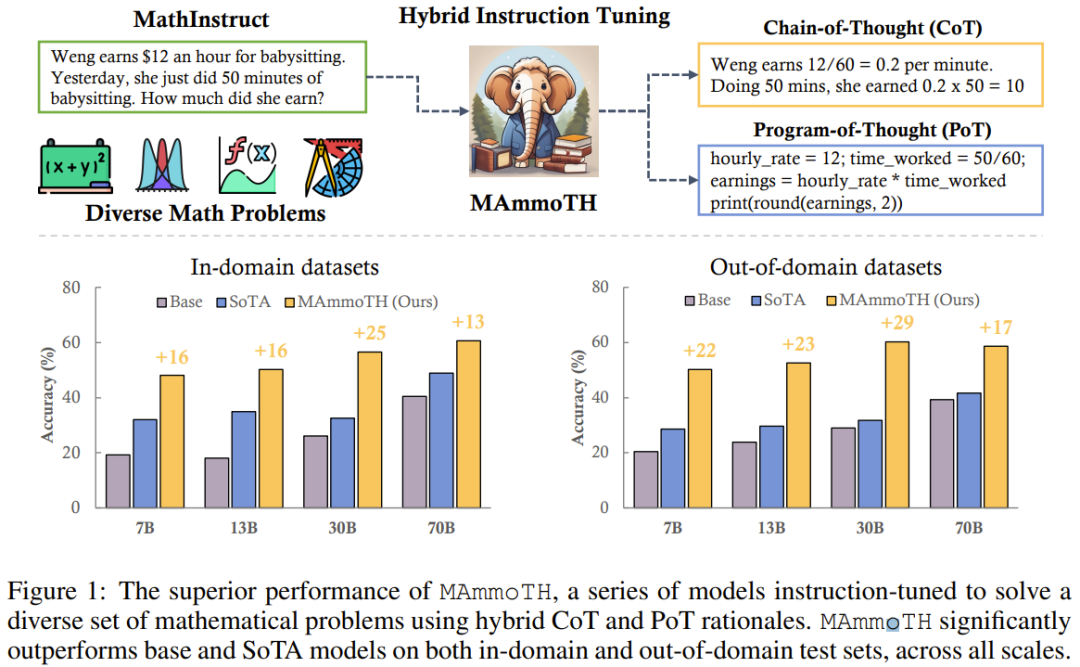
To evaluate MAmmoTH, the research team used a series of evaluation data sets, including an in-domain test set (GSM8K , MATH, AQuA-RAT, NumGLUE) and test sets outside the domain (SVAMP, SAT, MMLU-Math, Mathematics, SimulEq)

The research results show that the MAmmoTH model is generalized to It performs better on out-of-field data sets, and also significantly improves the ability of open source LLM in mathematical reasoning

It is worth noting that on the commonly used competition-level MATH data set, MAmmoTH The 7B version is able to beat WizardMath (the previous best open source model on MATH) by 3.5x (35.2% vs 10.7%), while the fine-tuned 34B MAmmoTH-Coder can even surpass GPT-4 using CoT

The contribution of this research can be summarized in two aspects: (1) In terms of data engineering, they proposed a high-quality mathematical instruction fine-tuning data set, which contains a variety of different Mathematical problems and mixing principles. (2) In terms of modeling, they trained and evaluated more than 50 different new models and baseline models ranging in size from 7B to 70B to explore the impact of different data sources and input-output formats

Research results show that new models such as MAmmoTH and MAmmoTH-Coder significantly exceed previous open source models in terms of accuracy

• Paper: https://arxiv.org/pdf/2309.05653.pdf
• ##Code: https:/ /github.com/TIGER-AI-Lab/MAmmoTH
• Datasets and models: https://huggingface.co/datasets/TIGER-Lab/MathInstruct

The team has released the data set they compiled, open sourced the code of the new method, and released the trained different sizes on Hugging Face The model

New proposed method

Reorganize a diverse mixed instruction fine-tuning dataset

The team’s goal is to compile a list of high-quality and diverse mathematical instruction fine-tuning datasets, which should have two main characteristics: (1) Broad coverage of different mathematical domains and complexity, (2) combining CoT and PoT principles.

For the first feature, the researchers first selected some widely used high-quality datasets involving different mathematical fields and complexity levels, such as GSM8K, MATH, AQuA , Camel and TheoremQA. They then noticed a lack of college-level mathematics, such as abstract algebra and formal logic, in existing datasets. To solve this problem, they used a small number of seed examples found online, used GPT-4 to synthesize the CoT principles of the questions in TheoremQA, and created "question-CoT" pairings in a self-guided manner

For the second feature, combining the CoT and PoT principles can improve the versatility of the data set, making the trained model capable of solving different types of mathematical problems. However, most existing datasets provide limited procedural rationales, resulting in an imbalance between CoT and PoT principles. To this end, the team used GPT-4 to supplement PoT principles for selected data sets, including MATH, AQuA, GSM8K and TheoremQA. These GPT-4 synthesized programs are then filtered by comparing their execution results with human-annotated ground truth, ensuring that only high-quality principles are added.

Following these guidelines, they created a new data set, MathInstruct, as detailed in Table 1 below.

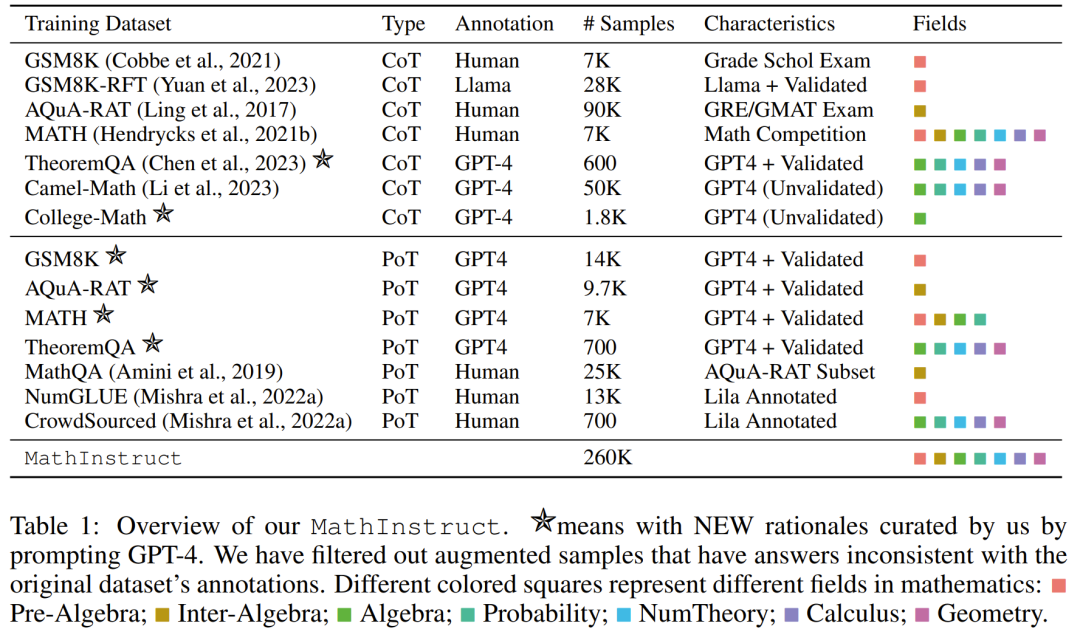
Contains 260,000 pairs (commands, responses) covering a wide range of core mathematical areas (arithmetic, algebra, probability, calculus and geometry etc.), contains a mix of CoT and PoT principles, and has different languages and difficulty levels.

Reset training

All subsets of MathInstruct have been unified into an Alpaca-like instruction data set structure. This standardization operation ensures that the fine-tuned model can handle the data consistently, regardless of the format of the original data set

For the base model, the team chose Llama-2 and Code Llama

By adjusting on MathInstruct, they obtained models of different sizes, including 7B, 13B, 34B and 70B

Experiment

Evaluation Dataset

To evaluate the mathematical reasoning ability of the model, the team selected some evaluation data sets, see below Table 2 contains many different in-field and out-of-field samples, covering several different areas of mathematics.

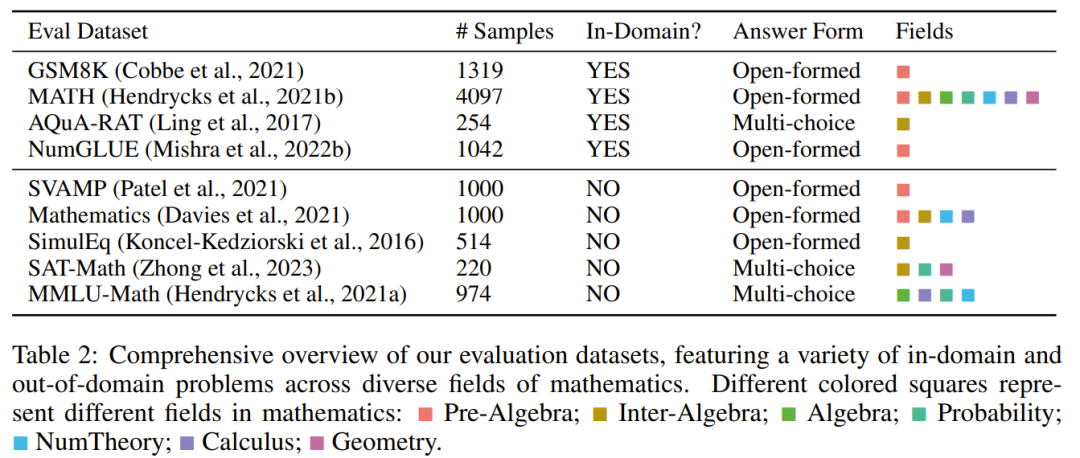
The assessment data set contains different difficulty levels, including primary, secondary and university levels. Some datasets also include formal logic and common sense reasoning

The assessment dataset chosen has both open-ended and multiple-choice questions.

For open-ended problems (such as GSM8K and MATH), researchers adopted PoT decoding because most of these problems can be solved programmatically. ,

For multiple-choice questions (such as AQuA and MMLU), the researchers adopted CoT decoding because most of the questions in this dataset can be better handled by CoT.

CoT decoding does not require any trigger words, while PoT decoding requires a trigger word: "Let’s write a program to solve the problem".

Main results

Tables 3 and 4 below report the results on data within and outside the domain, respectively.

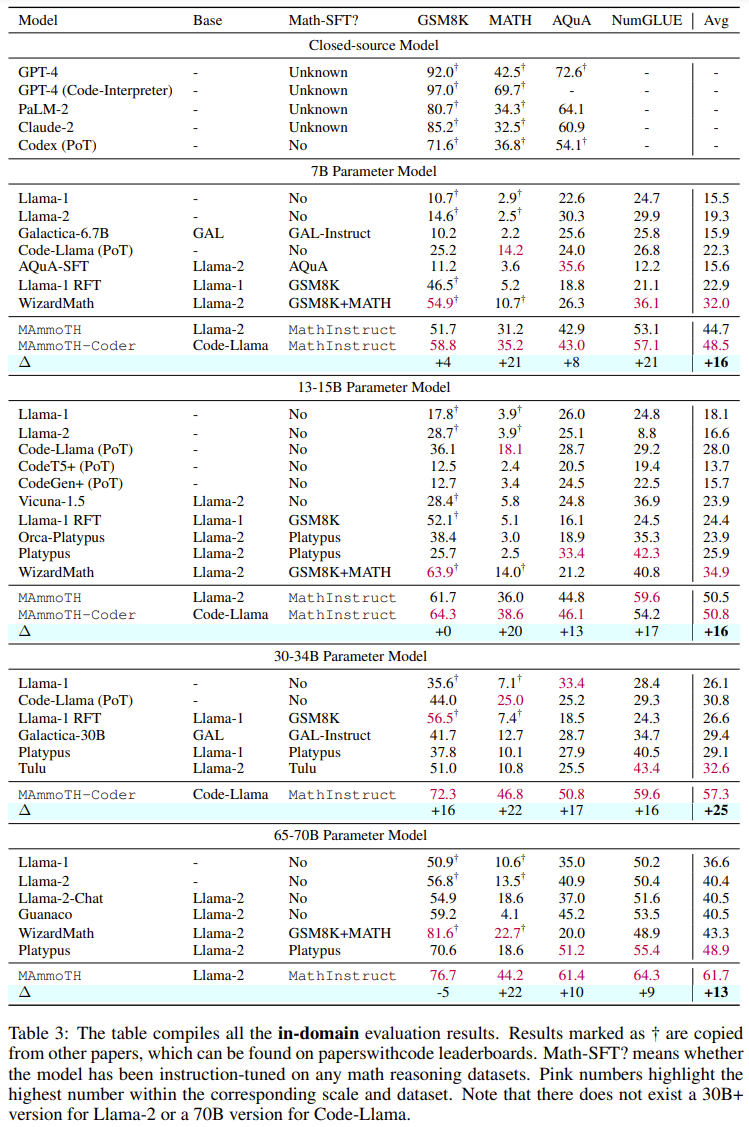
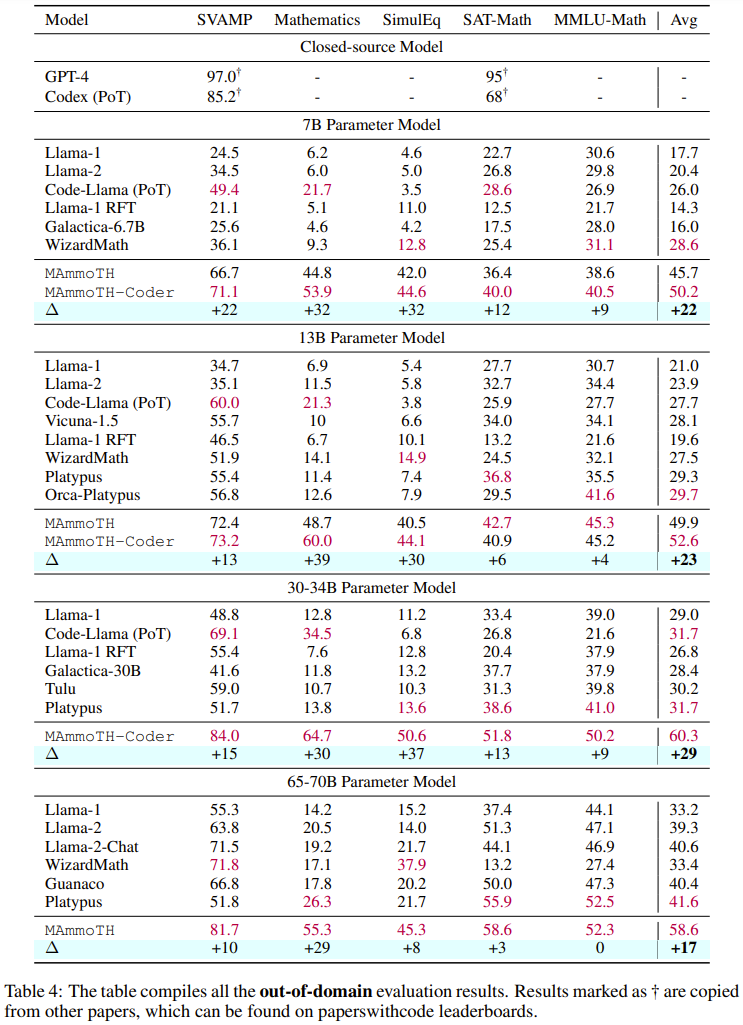
Overall, both MAmmoTH and MAmmoTH-Coder outperform the previous best models across different model sizes. The new model achieves more performance gains on out-of-domain datasets than on in-domain datasets. These results indicate that the new model does have the potential to become a mathematical generalist. MAmmoTH-Coder-34B and MAmmoTH-70B even outperform closed-source LLM on some datasets.

The researchers also compared using different base models. Specifically, they conducted experiments comparing two basic models, Llama-2 and Code-Llama. As can be seen from the above two tables, Code-Llama is overall better than Llama-2, especially on out-of-field data sets. The gap between MAmmoTH and MAmmoTH-Coder can even reach 5%

Exploration of ablation research on data sources

They conducted studies to explore the sources of performance gains. In order to better understand the source of MAmmoTH's advantages over existing benchmark models, the researchers conducted a series of controlled experiments. The results are shown in Figure 2

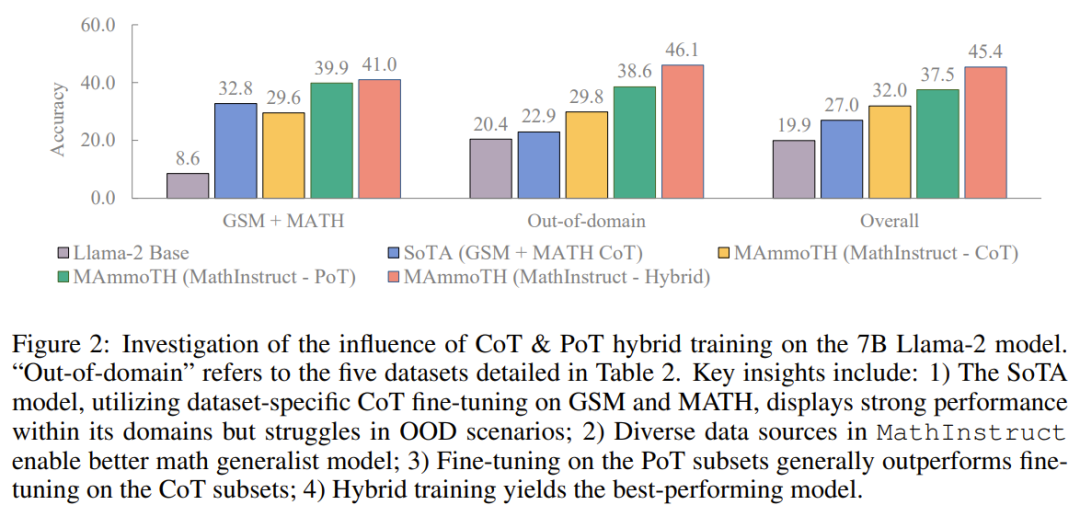
To summarize, the significant performance advantage of MAmmoTH can be attributed to: 1) diverse data sources covering different mathematical domains and complexity levels, 2) a hybrid strategy of CoT and PoT instruction fine-tuning.

They also studied the impact of major subsets. With regard to the diverse sources of MathInstruct used to train MAmmoTH, it is also important to understand the extent to which each source contributes to the overall performance of the model. They focus on four main subsets: GSM8K, MATH, Camel and AQuA. They conducted an experiment where each dataset was gradually added to training and compared performance to a model fine-tuned on the entire MathInstruct.

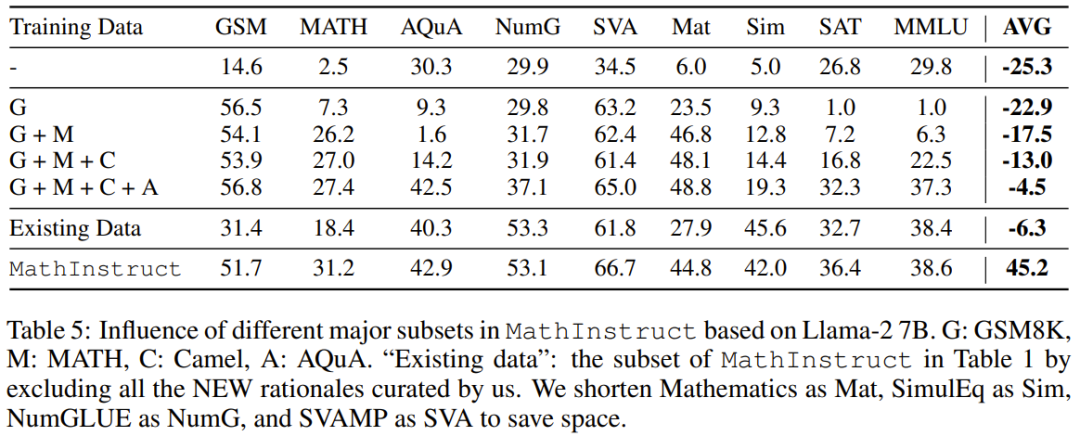
According to the results in Table 5, it can be seen that if the diversity of the training data set is insufficient (for example, when there is only GSM8K) , the generalization ability of the model is very poor: the model can only adapt to the situation within the data distribution, and it is difficult to solve problems other than GSM problems

The important impact of diverse data sources on MAmmoTH is in these Highlighted in the results is the core key to making MAmmoTH a mathematical generalist. These results also provide valuable insights and guidance for our future data curation and collection efforts, such as that we should always collect diverse data and avoid collecting only specific types of data

The above is the detailed content of Through MAmmoT, LLM becomes a mathematical generalist: from formal logic to four arithmetic operations. For more information, please follow other related articles on the PHP Chinese website!