Number of paths from root to leaves with at most M consecutive nodes and value K

Introduction

Binary trees are a fascinating data structure with a wide range of applications in computer science and programming. An interesting problem is to find the count from a given tree consisting of a parent node and its children. A binary tree is composed of nodes, the root node is determined, and the root node can provide child nodes according to user needs. The K value is determined, and the movement method is selected by the M value.

Count of root to leaf paths

The graph is created using various nodes that hold values ​​in the form of integers. This article mainly focuses on counting from the starting node or root node to the leaf node or child node.

Example

The graph is created from a binary tree with various nodes.

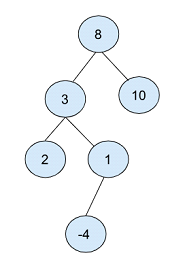
• In the above binary tree, the root node is selected as "8".

• Then create two nodes, one with a value of 3 and the other with a value of 10, occupying the left and right positions of the root node.

• With the node with value 2 as the root, create another child node with values ​​2 and 1 as left and right nodes respectively.

• Finally, a child node with a value of 1 creates a child node with a value of -4.

Method 1: C code to use a recursive function to compute a root-to-leaf path consisting of up to M consecutive nodes with K values

To solve this problem efficiently, we will utilize basic concepts such as tree traversal algorithm and recursion.

algorithm

Step 1: Create a structure to represent the tree node, which includes two pointers (left child node and right child node) and an integer field to store the node value.

Step 2: Design a recursive function to traverse the binary tree starting from the root, while tracking the current path length (initialized to 0), the number of consecutive occurrences (initially set to 0), and the target value K, allowing The maximum number of consecutive occurrences M.

Step 3: Call the function recursively on each left and right subtree, passing updated parameters such as incremental path length and number of consecutive occurrences (if applicable).

Step 4: For each non-empty node visited during the traversal:

a) If its value is equal to K, add one to both variables.

b) Reset the variable to zero if its value does not match K or exceeds the number of consecutive occurrences of M that have been encountered so far in the path.

Step 5: While traversing the tree, if the value of the child node is zero in both the left and right cases - we can handle it in two ways, namely

a) Check whether the variable does not exceed M.

b) If yes, increase the total number of paths that meet the condition by 1.

Example

//including the all in one header
#include<bits/stdc++.h>
using namespace std;
//creating structure with two pointers as up and down
struct Vertex {
   int data;
   struct Vertex* up;
   struct Vertex* down;
};
//countPaths function declared with five arguments ; with root = end; Node= vertex; left = up; right = down
int countPaths(Vertex* end, int K, int M, int currCount, int 
consCount) {
//To check the condition when the root is equal to 1 and greater than the maximum value, the values is incremented
   if (end == NULL || consCount > M) {
      return 0;
   }
//To check when the root is equal to the K value, increment by 1
   if (end->data == K) {
      currCount++;
      consCount++;
   } else {
//If it is not equal, it will return 0
      currCount = 0;
   }
   if (end->up == NULL && end->down == NULL) {
      if (currCount <= M) {
         return 1;
      } else {
         return 0;
      }
   }
   return countPaths(end->up, K, M, currCount, consCount) + countPaths(end->down, K, M, currCount, consCount);
}
//Main function to test the implementation
int main() {
   Vertex* end = new Vertex();
   end->data = 8;
   end->up = new Vertex();
   end->up->data = 3;
   end->down = new Vertex();
   end->down->data = 10;
   end->up->up = new Vertex();
   end->up->up->data = 2;
   end->up->down = new Vertex();
   end->up->down->data = 1;
   end->up->down->up = new Vertex();
   end->up->down->up->data = -4;

   int K = 1; // Value of node
   int M = 2; // Maximum consecutive nodes
   int currCount = -1; // Current count
   int consCount = -1; // Consecutive count

   cout << "The number of paths obtained from the given graph of" << M << "nodes with a value of " << K << " is " << countPaths(end, K, M, currCount, consCount) << endl;

   return 0;
} 

Output

The number of paths obtained from the given graph of 2 nodes with a value of 1 is 3

in conclusion

In this article, we explore the problem of counting the number of paths from the top (i.e., leaf) to the tip or root. Such problems can be solved efficiently by using tree traversal algorithms and recursive techniques in C. The process of traversing a binary tree may seem difficult, but it becomes easy with examples.

The above is the detailed content of Number of paths from root to leaves with at most M consecutive nodes and value K. For more information, please follow other related articles on the PHP Chinese website!