
"In a weighted directed graph G=(V,E), the weight of each edge is a real number. In addition, a vertex in V is also given, called the source.
Calculate the shortest path length from the source to all other vertices. This is the single source shortest path (SSSP) problem."
For more than half a century, researchers around the world have been trying to solve this problem. Now, the algorithmic puzzle has finally been successfully solved by a research team from the Department of Computer Science at the University of Copenhagen.
Negative weight SSSP algorithm: fast and efficient

Paper link: https:/ /arxiv.org/abs/2203.03456
In an interview, researcher Christian Wulff-Nilsen said that their solution is the first breakthrough that has existed for more than 30 years. The Õ(n(4/3) log W) operation time constrained SSSP combination algorithm with negative weights.
There are two classic algorithms about SSSP: Dijkstra algorithm (Dijkstra algorithm) and Bellman-Ford algorithm (Bellman-Ford algorithm), both All have their own limitations.
Dijkstra algorithm has the shortest operation time and can reach nearly linear time O(m n log n), but negative weight edges cannot be calculated.
The Bellman-Ford algorithm can calculate negative weight edges, but the operation time is too long, reaching O(mn). Currently, the state-of-the-art SSSP algorithms for solving negative-weighted edges rely on complex continuous optimization and dynamic algebraic and graphical algorithms. This leads to the fact that even if later generations of scholars continue to optimize the algorithm, its calculation time still takes Õ(n(4/3) log W). This computational time constraint has existed for thirty years.
Faced with these limitations, Wulff-Nilsen raised two questions:
## 1) Can the operation of the negative-weighted edge algorithm achieve near-linear time?
#2) Can this be achieved with simple tools?
#Is there a method that requires both time and quality?
#Don’t say it, it really does exist.
The algorithm proposed by Wulff-Nilsen is an image scaling algorithm, which is enhanced by the simple image decomposition algorithm Low Diameter Decomposition. Usually, this decomposition algorithm is only used for graph decomposition of non-negative-weighted edges, and one of the contributions of this research is to apply it to negative-weighted edge images to strengthen the negative-weighted edge SSSP recursive scaling algorithm.
Derivation processWulff-Nilsen is based on Johnson's price algorithm. Propose: In the image G = (V, E, w), let Φ be any function: V→ Z. Let w(Φ) be the weight function:
Definition: , : . In imageG = (V, E,w) and imageG' = (V, E,w'), if: 1) The shortest distance between the image G and the image The shortest distance in G' is equal and vice versa; 2) G is only in G'## When # contains a negative weight ring, the image G is equal to the image G'.
Corollary 2.7 Consider an arbitrary image 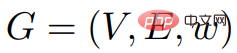 and a price function Φ. In u, v ∈ V,
and a price function Φ. In u, v ∈ V,
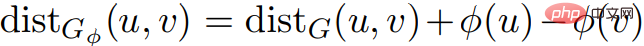 . And in any ring C,
. And in any ring C,
. 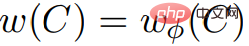 Therefore, G is equal to
Therefore, G is equal to 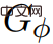 . If ##,
. If ##, 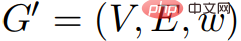 ,
, 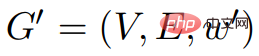
 then G and G'Equal.
then G and G'Equal.
The purpose of this algorithm is to calculate the price function Φ when # All edge weights in ##GΦ are non-negative, assuming there is no negative weight cycle. Then you can run Dijkstra's algorithm on . 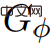
First, Wulff-Nilsen assumes that there is an algorithm Dijkstra (
G,s), inputting a graph without negative weight edgesG, vertex s ∈ V, s in G outputs the shortest path tree. The running time is O(m n log n). If G is a DAG (directed acyclic graph), calculate a price function Φ such that The objective of the single-source shortest path problem is to find the shortest path from a given starting node to all other nodes in the network. #A network is represented as a graph consisting of nodes and the connections between them, called edges. Each edge has a direction (for example, this can be used to represent a one-way road) and a weight that represents the cost of traveling along that edge. If all edge weights are non-negative, the problem can be solved in almost linear time using the classic Dijkstra's algorithm. The new results solve this problem in almost the same time as Dijkstra's algorithm, but also allow for negative edge weights. After that, Wulff-Nilsen mentioned the two most important algorithms in combination tools: ScaleDown and SPmain . ##The ScaleDown algorithm runs in stages, and in the last stage it uses ElimNeg () to calculate the price function This means that, for all , If the algorithm terminates, then for all This means that for all By induction, assuming that the theory applies to Therefore, through the Output of Since Thus we can conclude that if #This can prove the correctness of the SPmain algorithm. So far, the two most important algorithms in Wulff-Nilsen's negative weight SSSP solution have been proven to be true. The new algorithm successfully introduces negative weights while ensuring near-linear time. Last year, Wulff -Nilsen made another breakthrough in the same field, involving how to find shortest paths in time-varying networks. His solution to a recent riddle builds on this work. He believes that solving the SSSP problem can pave the way for algorithms that can not only help electric vehicles instantly calculate the fastest route to their destination, but also ensure that The most energy efficient way to do this. Wulff-Nilsen explained: “Our algorithm adds negative weights, a dimension that previous algorithms did not have. A practical example is when driving in the mountains. , with the dimension of negative weight, the navigation system can recommend routes with more downhill roads to electric vehicle owners, so that electric vehicles can be charged when going downhill." Wulff-Nilsen also said that their algorithm can not only be used for electric vehicle route planning, but also for monitoring speculation in the financial industry. He said: "In principle, this algorithm can be used to provide early warning to users such as central banks, warning speculators speculating in the purchase and sale of various currencies. Now, many criminals use computers to commit crimes, but because our algorithm is so fast, it may be possible It is used to monitor and detect vulnerabilities before they are exploited." In 1959, when Dijkstra first proposed the shortest distance problem, he probably would not have thought of it. , for more than 60 years, some people have been constantly optimizing the solution to this problem. You may also be surprised that the answer to the puzzle has such rich connotations. #Perhaps, this is the charm of science.  has Non-negative edge weights are simple: just loop over v1, ..., vn of the topology and set Φ(vi) so that all incoming edge weights are non-negative.
has Non-negative edge weights are simple: just loop over v1, ..., vn of the topology and set Φ(vi) so that all incoming edge weights are non-negative. 
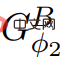 Φ2. If ElimNeg terminates, it will return the price function ψ′, let
Φ2. If ElimNeg terminates, it will return the price function ψ′, let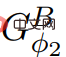 all edge values are non Negative; in other words, because ,
all edge values are non Negative; in other words, because , 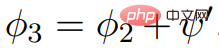 , does not contain negative weights.
, does not contain negative weights. 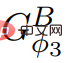
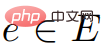 satisfies the condition (because
satisfies the condition (because 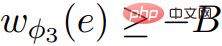 ). This proves the correctness of the ScaleDown output.
). This proves the correctness of the ScaleDown output. 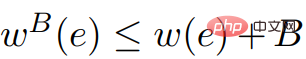

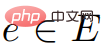 and
and 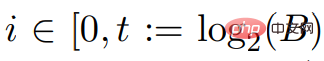 ,
, 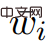 is the integral and for all
is the integral and for all  ,
, 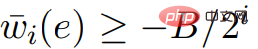 .
. 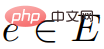 ,
, 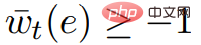 . Therefore the graph G* has non-negative weights.
. Therefore the graph G* has non-negative weights. 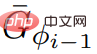 , The response to ScaleDown in line 5 of the algorithm The call to
, The response to ScaleDown in line 5 of the algorithm The call to 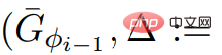
 # meets the necessary input attributes.
# meets the necessary input attributes. 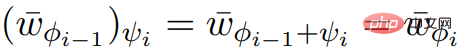 and ScaleDown, you can get
and ScaleDown, you can get 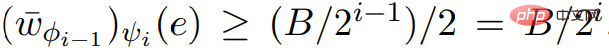 .
. 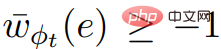 , if C is
, if C is 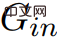 ## In any negative weight cycle, since all the values of in
## In any negative weight cycle, since all the values of in  are multiples of 2n, and ;
are multiples of 2n, and ; 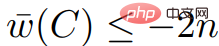 also We know ,
also We know , 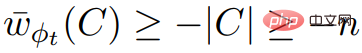 , so
, so 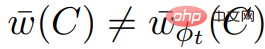 is inconsistent with Corollary 2.7.
is inconsistent with Corollary 2.7. 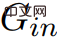 contains a negative weight cycle, the algorithm will not terminate.
contains a negative weight cycle, the algorithm will not terminate.
The above is the detailed content of A puzzle from 60 years ago! Researchers from the University of Copenhagen solve the 'single source shortest path' problem. For more information, please follow other related articles on the PHP Chinese website!




