Detailed explanation of depth-first traversal of binary trees in Java

In the past two days, I have been doing algorithm questions related to binary trees and taking some study notes. (You don’t even know how to do binary trees? You are really not proficient, and you don’t have to write algorithms or data structures related to binary trees in your daily work. Because I am good at it, I have to study harder!)

Definition

Let’s first look at Wikipedia’s explanation: In computer science, Binary tree (English: Binary tree) is a node with at most two branches ( That is, there is no tree structure with a node with a branch degree greater than 2). Usually branches are called "left subtree" or "right subtree". The branches of a binary tree have left and right order and cannot be reversed at will.

Due to the characteristics defined by the binary tree itself, it has a high degree of local repeatability, so when traversing the binary tree depth-first, it is usually implemented in a recursive way. The code implemented in this way is very concise and beautiful, and it is easier to understand. .

Depth-first traversal

Generally, we have three most common order traversals for depth-first traversal of binary trees: pre-order, mid-order, and post-order.

The traversal order of the preorder is: visit the root node-> traverse the left subtree-> traverse the right subtree

The traversal order of the mid-order is: traverse the left subtree-> ; Access the root node-> Traverse the right subtree

The post-order traversal order is: Traverse the left subtree-> Traverse the right subtree-> Visit the root node

Note The left and right here are the entire subtree, not a node, because we need to traverse the entire tree, so each traversal is performed in this order until the leaf node.

For example, if there is the following binary tree:

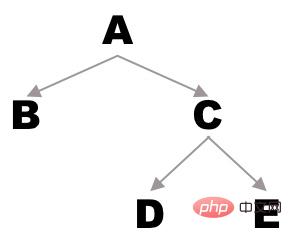
The sequence obtained by preorder traversal is A - B - C - D - E

The sequence obtained by mid-order traversal is B - A - D - C - E

The sequence obtained by post-order traversal is B - D - E - C - A

We will use pre-order traversal. (It is strongly not recommended to use human recursion, at least my brain can’t handle three levels...):

First level of recursion:

Visit the root node first, so the root node is output A, then traverse the left subtree (L1), and then traverse the right subtree (R1);

Second level recursion:

For L1, the root node is visited first, so the output is at this time The root node B, and then find that the left and right subtrees of B are empty, end the recursion;

For R1, visit the root node first, so output the root node C at this time, and then traverse the left subtree ( L2), and then traverse the right subtree (R2);

The third level of recursion:

For L2, the root node is visited first, so the root node D at this time is output, and then found The left and right subtrees of D are empty, and the recursion ends;

For R2, the root node is visited first, so the root node E at this time is output, and then the left and right subtrees of E are found to be empty, and the recursion ends;

Characteristics of front, middle and back order

According to the definition of front, middle and back order, it is not difficult for us to find the following characteristics:

• The first one in the pre-order must be the root node, and the last one in the post-order must be the root node

• The distribution of the left subtree and right subtree of each sort is regular

• For each subtree, a tree that follows the above two rules

#These characteristics are the expression of the order in the definition.

Various derivation

Here are some of the most basic algorithm questions for binary tree traversal:

• Given a binary tree, get the sequence of its pre/middle/post-order traversal;

• Derivation of the post-order (or derivation of the entire binary tree) based on the pre-order and mid-order;

• Based on the post-order and in-order to deduce pre-order (or deduce the entire binary tree);

For binary tree traversal, as mentioned before, recursion is usually used. For recursion, there are templates that can be applied directly:

public void recur(int level, int param) {
    
    // terminator
    if (level > MAX_LEVEL) {
        // process result
         return;   
    }
    
    // process current logic
    process(level, param);
    
    // drill down
    recur(level+1, newParam);
    
    // restore current status
}

This is a more practical tip mentioned by Brother Chao (Qin Chao) in the algorithm training camp I watched in the past two days (this template is especially good for novices). Follow the three steps above (if there are local variables needed Release or additional processing will be done in step 4) You can write recursive code in a more orderly manner.

Here is an example of deriving post-order based on pre-order and mid-order:

First initialize the two sequences:

int[] preSequence = {1, 2, 3, 4, 5, 6, 7, 8, 9};
int[] inSequence = {2, 3, 1, 6, 7, 8, 5, 9, 4};

Through the several features mentioned above, we have The minimum repeated sub-problem can be found. Each recursion

matches the index i where the node value is located in the mid-order according to the first node value of the previous sequence, so that we We can get the front and back parts of index i corresponding to the left and right subtrees respectively, and then traverse the two left and right subtrees respectively, and then output the first node value of the current preorder, which is the root node.

According to the top-down programming method, we can first write the following initial recursive call:

List<Integer> result = new ArrayList<>();
preAndInToPost(0, 0, preSequence.length, preSequence, inSequence, result);

The first parameter represents the first element index of the preorder sequence;

The second parameter represents the first element index of the in-order sequence;

The third parameter represents the length of the sequence;

第四个参数表示前序序列；

第五个参数表示后序序列；

第六个参数用于保存结果；

先来考虑终止条件是什么，也就是什么时候结束递归，当我们的根结点为空的时候终止，对应这里就是序列长度为零的时候。

if (length == 0) {
    return;
}

接着考虑处理逻辑，也就是找到索引 i：

int i = 0;
while (inSequence[inIndex + i] != preSequence[preIndex]) {
    i++;
}

然后开始向下递归：

preAndInToPost(preIndex + 1, inIndex, i, preSequence, inSequence, result);
preAndInToPost(preIndex + i + 1, inIndex + i + 1, length - i - 1, preSequence, inSequence, result);
result.add(preSequence[preIndex]);

因为推导的是后序序列，所以顺序如上，添加根结点的操作是在最后的。前三个参数如何得出来的呢，我们走一下第一次遍历就可以得出来。

前序序列的第一个结点 1 在中序序列中的索引为 2，此时

左子树的中序系列起始索引为总序列的第 1 个索引，长度为 2；

左子树的前序序列起始索引为总序列的第 2 个索引，长度为 2；

右子树的中序系列起始索引为总序列的第 3 个索引，长度为 length - 3；

右子树的前序序列起始索引为总序列的第 3 个索引，长度为 length - 3；

完整代码如下：

/**
 * 根据前序和中序推导后序
 *
 * @param preIndex    前序索引
 * @param inIndex     中序索引
 * @param length      序列长度
 * @param preSequence 前序序列
 * @param inSequence  中序序列
 * @param result      结果序列
 */
private void preAndInToPost(int preIndex, int inIndex, int length, int[] preSequence, int[] inSequence, List<Integer> result) {
    if (length == 0) {
        return;
    }

    int i = 0;
    while (inSequence[inIndex + i] != preSequence[preIndex]) {
        i++;
    }

    preAndInToPost(preIndex + 1, inIndex, i, preSequence, inSequence, result);
    preAndInToPost(preIndex + i + 1, inIndex + i + 1, length - i - 1, preSequence, inSequence, result);
    result.add(preSequence[preIndex]);
}

参考链接

• 维基百科 - 二叉树（https://zh.wikipedia.org/wiki/%E4%BA%8C%E5%8F%89%E6%A0%91）

推荐教程：《java教程》

The above is the detailed content of Detailed explanation of depth-first traversal of binary trees in Java. For more information, please follow other related articles on the PHP Chinese website!