這篇文章主要介紹了python實現希爾排序,已編程實現的希爾排序,具有一定的參考價值,有興趣的小伙伴們可以參考一下
觀察一下」插入排序“ :其實不難發現她有個缺點:
如果當資料是」5, 4, 3, 2, 1「的時候,此時我們將「無序區塊」中的記錄插入「有序塊」時,估計俺們要崩盤,每次插入都要移動位置,此時插入排序的效率可想而知。
shell根據這個弱點進行了演算法改進,融入了一種叫做「縮小增量排序法」的思想,其實也蠻簡單的,不過有點注意的就是:
增量不是亂取,而是有規律可循的。
希爾排序時效分析很難,關鍵碼的比較次數與記錄移動次數依賴於增量因子序列d的選取,特定情況下可以準確估算出關鍵碼的比較次數和記錄的移動次數。目前還沒有人給出選取最好的增量因子序列的方法。增量因子序列可以有各種取法,有取奇數的,也有取質數的,但需要注意:增量因子中除1 外沒有公因子,且最後一個增量因子必須為1 。希爾排序方法是一個不穩定的排序方法。
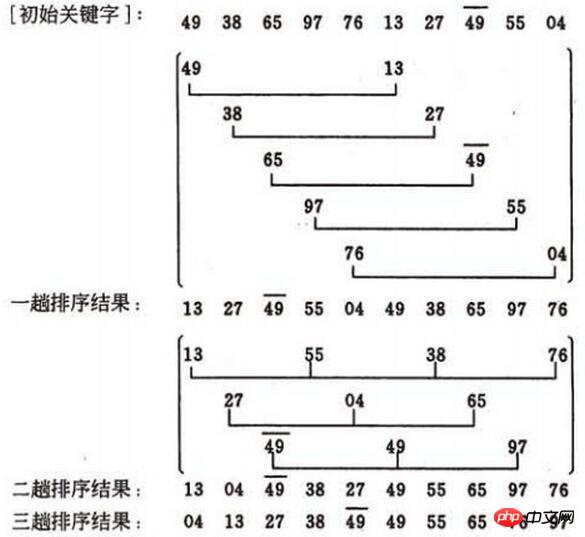
首先要先明確一下增量的取法(這裡圖片是copy別人博客的,增量是奇數,我下面的編程用的是偶數):
第一次增量的取法為: d=count/2;
第二次增量的取法為: d=(count/2)/2;
最後一至: d=1;
#好,注意看圖了,第一趟的增量d1=5, 將10個待排記錄分為5個子序列,分別進行直接插入排序,結果為(13, 27, 49, 55, 04, 49, 38, 65, 97, 76)
第二趟的增量d2=3, 將10個待排記錄分為3個子序列,分別進行直接插入排序,結果為(13, 04, 49, 38, 27, 49, 55, 65, 97, 76)
第三趟的增量d3=1, 對整個序列進行直接插入排序,最後結果為(04, 13, 27, 38, 49, 49, 55, 65, 76, 97)
重點來了。當增量減少到1時,此時序列已基本有序,希爾排序的最後一趟就是接近最好情況的直接插入排序。可將前面各趟的"宏觀"調整看成是最後一趟的預處理,比只做一次直接插入排序效率更高。
本人是學python的,今天用python實作了希爾排序。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
|
輸出:
>: [49, 38, 65, 97, 76, 13, 27, 49, 55, 4]
>>: [13, 27, 49, 55, 4, 49, 38, 65, 97, 76]
>>: [4, 27, 13, 49, 38, 55, 49, 65, 97, 76]
>>: [4, 13, 27, 38, 49, 49, 55, 65, 76, 97]
#首先你得先插入排序,不會你必然看不懂。
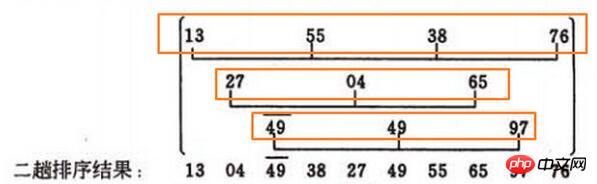
插入排序,也就是將上方圖三個黃色方塊中的數字插入排序。舉例:13,55,38,76
直接看55,55<13, 不用移動。接著看38,38<55,那麼55後移,資料變成[13,55,55,76],接著比較13<38, 那麼38替換55,變成[13,38,55,76]。其它同理,略。
這裡有個問題,例如第二個黃色框[27,4,65],4<27, 那27往後移,接著4就替換第一個,資料變成[ 4,27,65],但是計算機怎麼知道4就是在第一個啊??
我的做法是,先找出[27,4,65]第一個數的下標,在這個例子中27的下標為1。當要插入的數的下標大於第一個下標1時,才可以往後移,前一個數不可以往後移有兩種情況,一種是前面有數據,且小於要插入的數,那你只能插在它後面。另一種,很重要,當要插入數比前面所有數都小時,那插入數肯定是放在第一個,此時要插入數的下標=第一個數的下標。 (這段話,感覺初學者應該不大懂…)
為了找到第一個數的下標,最開始想的是用循環,一直到最前面:
1 2 3 4 |
|
在Debug時,發現用循環太浪費時間了,特別是當增量d=1時,直接插入排序為了插入列表最後一個數,得循環減1,直到第一個數的下標,後來我學聰明了,用下面的方法:
1 2 |
|
時間複雜度:
希爾排序的時間複雜度是所取增量序列的函數,尚難準確分析。有文獻指出,當增量序列為d[k]=2^(t-k+1)時,希爾排序的時間複雜度為O(n^1.5), 其中t為排序趟數。
穩定性: 不穩定
希爾排序效果:
參考資料: 程式設計是我自己實現的。建議Debug看看運行過程
c++中八大排序演算法
視覺直覺感受若干常用排序演算法
C#七大經典排序演算法系列(下)
1.非系統的學習也是在浪費時間2.做一個會欣賞美,懂藝術,會藝術的技術人
以上是python實作希爾排序的實例詳解的詳細內容。更多資訊請關注PHP中文網其他相關文章!




