Python에서 피보나치 수열을 구현하는 방법의 예-파이썬 튜토리얼-php.cn

Python에서 피보나치 수열을 구현하는 방법의 예

高洛峰

풀어 주다： 2017-01-14 16:48:12

원래의

2377명이 탐색했습니다.

소개

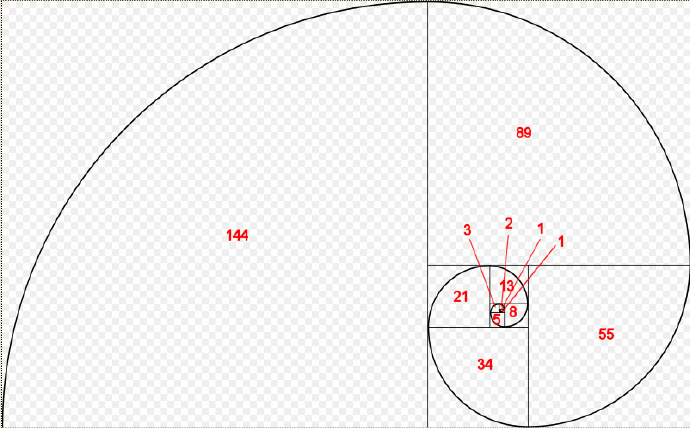
황금분할 수열이라고도 알려진 피보나치 수열은 0, 1, 1, 2, 3, 5, 8, 13, 21,... 등의 수열을 말합니다. 수학적으로 피보나치 수열은 다음과 같이 재귀적으로 정의됩니다.

F(0)=0, F(1)=1, F(n)=F(n-1)+F(n -2) ( n≥2, n∈N*).

Python에서 피보나치 수열을 구현하는 방법의 예

1. 튜플 구현

fibs = [0, 1]
for i in range(8):
 fibs.append(fibs[-2] + fibs[-1])

로그인 후 복사

지정된 범위 내의 피보나치 수 목록을 가져올 수 있습니다.

2. 반복자

class Fibs:
 def __init__(self):
  self.a = 0
  self.b = 1
 
 def next(self):
  self.a, self.b = self.b, self.a + self.b
  return self.a
 
 def __iter__(self):
  return self

로그인 후 복사

를 구현하면 다음과 같이 액세스할 수 있는 무한 시퀀스가 생성됩니다.

fibs = Fibs()
for f in fibs:
 if f > 1000:
  print f
  break
 else:
  print f

로그인 후 복사

3. 사용자 정의를 통해

class Fib(object):
 def __getitem__(self, n):
  if isinstance(n, int):
   a, b = 1, 1
   for x in range(n):
    a, b = b, a + b
   return a
  elif isinstance(n, slice):
   start = n.start
   stop = n.stop
   a, b = 1, 1
   L = []
   for x in range(stop):
    if x >= start:
     L.append(a)
    a, b = b, a + b
   return L
  else:
   raise TypeError("Fib indices must be integers")

로그인 후 복사

<를 구현합니다. class 🎜>이런 방식으로 시퀀스와 유사한 데이터 구조를 얻을 수 있으며 아래 첨자를 통해 데이터에 액세스할 수 있습니다.

f = Fib()
print f[0:5]
print f[:10]

로그인 후 복사

4. 비교적 간단한 피보나치 수열 예제의 Python 구현

먼저 피보나치 수열을 살펴보세요...

0 1 1 2 3 5 8 13 21 34 55 89 144 233...

로그인 후 복사

먼저 처음 두 변수에 값을 할당합니다:

i, j = 0, 1

로그인 후 복사

물론 다음과 같이 작성할 수도 있습니다. this:

i = 0
j = 1

로그인 후 복사

그런 다음 범위를 설정하고 10000 이내에서 준비됩니다.

while i < 10000:

로그인 후 복사

그런 다음 while 문에 i를 출력하고 논리를 설계합니다.

print i,
i, j = j, i+j

로그인 후 복사

주의가 필요합니다. 여기서: "i, j = i, i+j" 코드 다음과 같이 쓸 수 없습니다:

i = j
j = i+j

로그인 후 복사

이렇게 쓰면 j는 처음 두 자리의 덧셈 값이 아니지만, j에 의해 값이 할당된 i와 j를 더한 값입니다. 이 경우 출력 시퀀스는 다음과 같습니다.

0 1 2 4 8 16 32 64 128 256 512 1024 2048 4096 8192

로그인 후 복사

올바른 전체 코드는 다음과 같습니다.

i, j = 0, 1
while i < 10000:
 print i,
 i, j = j, i+j

로그인 후 복사

마지막으로 실행 결과가 표시됩니다.

0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765

로그인 후 복사

요약

위 내용은 모두 Python을 사용하여 피보나치 수열을 구현하는 내용입니다. 이 글의 내용이 모든 분들의 공부나 업무에 조금이나마 도움이 될 수 있으니 궁금한 점이 있으시면 메시지를 남겨주세요.

Python에서 피보나치 수열을 구현하는 방법에 대한 더 많은 예와 관련 기사를 보려면 PHP 중국어 웹사이트를 주목하세요!