π는 수많은 사람들이 따라다니는 진정한 마법의 숫자입니다. 영원히 반복되는 무리수에 대해 무엇이 그렇게 매력적인지 잘 모르겠습니다. 제 생각에는 π를 계산하는 것, 즉 π의 값을 계산하는 것을 좋아합니다. π는 무리수이므로 무한합니다. 이는 π 계산이 근사치일 뿐이라는 것을 의미합니다. 100자리를 계산하면 101자리를 계산할 수 있고 더 정확해집니다. 지금까지 일부에서는 가장 정확한 π를 계산하기 위해 슈퍼컴퓨터를 선택했습니다. 일부 극단값에는 5억 자릿수 파이 계산이 포함됩니다. 100억 자리의 π가 포함된 텍스트 파일을 온라인에서 찾을 수도 있습니다(주의하세요! 이 파일은 다운로드하는 데 시간이 걸릴 수 있으며 일반적인 메모장 응용 프로그램에서는 열리지 않습니다.). 저는 몇 줄의 간단한 Python으로 π를 계산하는 방법에 관심이 있습니다.

언제든지 math.pi 변수를 사용할 수 있습니다. 이는 표준 라이브러리에 포함되어 있으므로 직접 계산하기 전에 이를 사용해야 합니다. 실제로 우리는 이를 정확도를 계산하는 데 사용할 것입니다. 먼저 Pi를 계산하는 매우 간단한 방법을 살펴보겠습니다. 늘 그렇듯이 저는 Python 2.7을 사용할 예정이며, 동일한 아이디어와 코드가 다른 버전에도 적용될 수 있습니다. 우리가 사용할 대부분의 알고리즘은 Pi WikiPedia 페이지에서 가져오고 구현됩니다. 다음 코드를 살펴보겠습니다.
importsys
importmath
defmain(argv):
iflen(argv) !=1:
sys.exit('Usage: calc_pi.py <n>')
print'\nComputing Pi v.01\n'
a=1.0
b=1.0/math.sqrt(2)
t=1.0/4.0
p=1.0
foriinrange(int(sys.argv[1])):
at=(a+b)/2
bt=math.sqrt(a*b)
tt=t-p*(a-at)**2
pt=2*p
a=at;b=bt;t=tt;p=pt
my_pi=(a+b)**2/(4*t)
accuracy=100*(math.pi-my_pi)/my_pi
print"Pi is approximately: "+str(my_pi)
print"Accuracy with math.pi: "+str(accuracy)
if__name__=="__main__":
main(sys.argv[1:])이것은 원하는 대로 다운로드하고, 실행하고, 수정하고, 다른 사람과 공유할 수 있는 매우 간단한 스크립트입니다. 다음과 유사한 출력을 볼 수 있습니다.
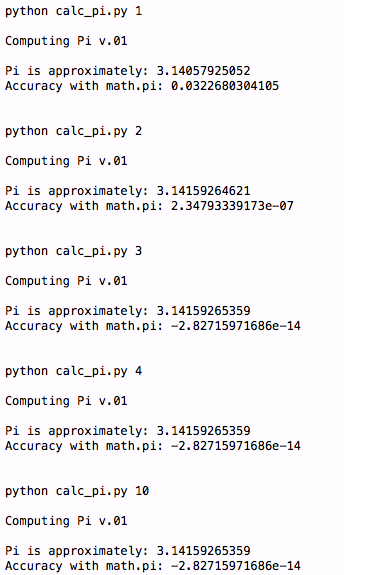
n이 4보다 크더라도 우리는 Pi 정확도에 접근하지만 크게 개선되지는 않습니다. n의 값이 더 커진다고 해도 같은 일(pi의 근사 정확도는 향상되지 않음)이 계속 발생할 것이라고 추측할 수 있습니다. 다행히도 이 수수께끼를 풀 수 있는 방법은 여러 가지가 있습니다. Python Decimal(십진수) 라이브러리를 사용하면 Pi에 가까운 더 높은 정밀도의 값을 얻을 수 있습니다. 라이브러리 함수가 어떻게 사용되는지 살펴보겠습니다. 이 단순화된 버전은 11자리 이상의 숫자를 얻을 수 있으며 일반적으로 Python 부동 소수점 숫자보다 정밀도가 낮습니다. 다음은 Python Decimal 라이브러리의 예입니다.

이 숫자를 참조하세요. 잘못된! 3.14만 입력했는데 왜 정크가 나왔나요? 이것은 메모리 쓰레기입니다. 간단히 말해서 Python은 원하는 십진수와 약간의 추가 값을 제공합니다. 처음에 정밀도가 이전 정크 번호보다 작으면 계산에 영향을 미치지 않습니다. getcontext().prec를 설정하여 원하는 자릿수를 지정할 수 있습니다. 시도해 봅시다.
아주 좋아요. 이제 이것을 사용하여 이전 코드에 대한 더 나은 근사치를 얻을 수 있는지 살펴보겠습니다. 저는 일반적으로 " from library import * "를 사용하는 것을 반대하지만 이 경우에는 코드가 더 예뻐 보입니다.
importsys
importmath
fromdecimalimport*
defmain(argv):
iflen(argv) !=1:
sys.exit('Usage: calc_pi.py <n>')
print'\nComputing Pi v.01\n'
a=Decimal(1.0)
b=Decimal(1.0/math.sqrt(2))
t=Decimal(1.0)/Decimal(4.0)
p=Decimal(1.0)
foriinrange(int(sys.argv[1])):
at=Decimal((a+b)/2)
bt=Decimal(math.sqrt(a*b))
tt=Decimal(t-p*(a-at)**2)
pt=Decimal(2*p)
a=at;b=bt;t=tt;p=pt
my_pi=(a+b)**2/(4*t)
accuracy=100*(Decimal(math.pi)-my_pi)/my_pi
print"Pi is approximately: "+str(my_pi)
print"Accuracy with math.pi: "+str(accuracy)
if__name__=="__main__":
main(sys.argv[1:])출력 결과:
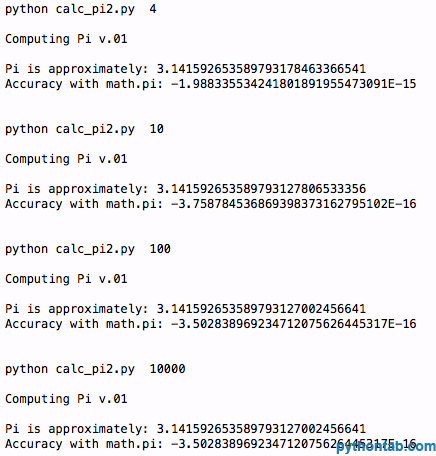
그렇습니다. 우리는 더 정확하지만 약간의 반올림이 있는 것 같습니다. n = 100과 n = 1000에서는 동일한 정확도를 갖습니다. 지금은 무엇입니까? 좋아요, 이제 공식을 살펴보겠습니다. 지금까지 우리가 Pi를 계산한 방식은 부분을 더하는 것이었습니다. Pi 계산에 관한 DAN의 기사에서 일부 코드를 찾았습니다. 그는 다음 3가지 공식을 사용할 것을 제안했습니다.
Bailey–Borwein–Plouffe 공식
Bellard의 공식
Chudnovsky 알고리즘
Bailey부터 시작하겠습니다. Borwein –Plouffe 공식이 시작됩니다.
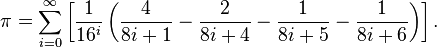
코드에서는 다음과 같이 작성할 수 있습니다.
import sys
import math
from decimal import *
def bbp(n):
pi=Decimal(0)
k=0
while k < n:
pi+=(Decimal(1)/(16**k))*((Decimal(4)/(8*k+1))-(Decimal(2)/(8*k+4))-(Decimal(1)/(8*k+5))-(Decimal(1)/(8*k+6)))
k+=1
return pi
def main(argv):
if len(argv) !=2:
sys.exit('Usage: BaileyBorweinPlouffe.py <prec> <n>')
getcontext().prec=(int(sys.argv[1]))
my_pi=bbp(int(sys.argv[2]))
accuracy=100*(Decimal(math.pi)-my_pi)/my_pi
print"Pi is approximately "+str(my_pi)
print"Accuracy with math.pi: "+str(accuracy)
if __name__=="__main__":
main(sys.argv[1:])"래퍼" 코드인 BBP(N)는 제쳐두고 기능은 당신이 정말로 원하는 것입니다. N을 더 크게 지정하고 getcontext().prec에 더 큰 값을 설정할수록 계산이 더 정확해집니다. 몇 가지 코드 결과를 살펴보겠습니다.
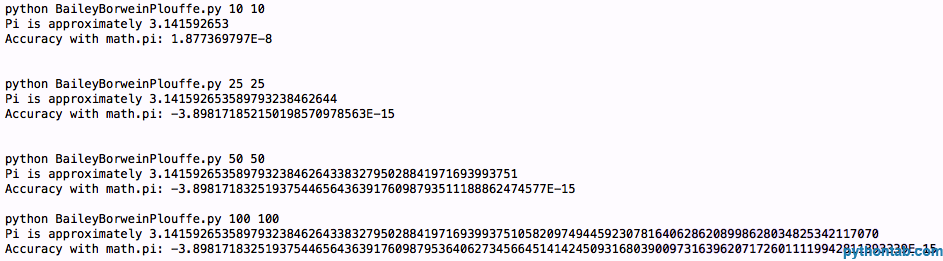
숫자가 너무 많습니다. 이전보다 더 정확하지 않다는 것을 알 수 있습니다. 따라서 우리는 다음 공식인 Bellah의 공식으로 넘어가서 더 나은 정확도를 얻을 필요가 있습니다. 다음과 같습니다:
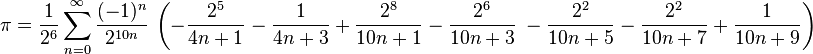
변환 공식만 변경하고 나머지 코드는 동일하게 유지합니다. Python으로 구현된 Bella의 공식을 다운로드하려면 여기를 클릭하세요. bellards(n)을 살펴보겠습니다:
def bellard(n):
pi=Decimal(0)
k=0
while k < n:
pi+=(Decimal(-1)**k/(1024**k))*( Decimal(256)/(10*k+1)+Decimal(1)/(10*k+9)-Decimal(64)/(10*k+3)-Decimal(32)/(4*k+1)-Decimal(4)/(10*k+5)-Decimal(4)/(10*k+7)-Decimal(1)/(4*k+3))
k+=1
pi=pi*1/(2**6)
return pi출력:
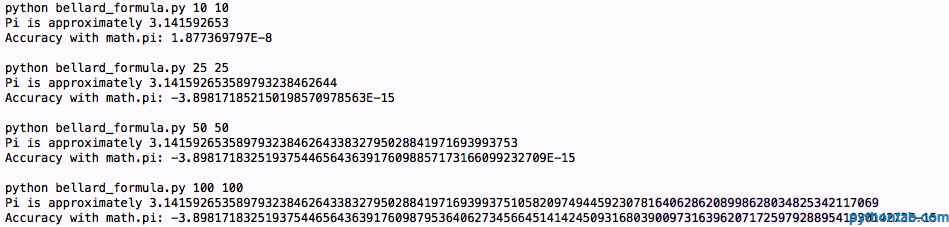
哦,不,我们得到的是同样的精度。好吧,让我们试试第三个公式, Chudnovsky 算法,它看起来是这个样子:
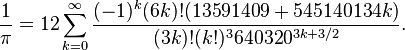
再一次,让我们看一下这个计算公式(假设我们有一个阶乘公式)。 点击这里可下载用 python 实现的 Chudnovsky 公式。
下面是程序和输出结果:
def chudnovsky(n):
pi=Decimal(0)
k=0
while k < n:
pi+=(Decimal(-1)**k)*(Decimal(factorial(6*k))/((factorial(k)**3)*(factorial(3*k)))*(13591409+545140134*k)/(640320**(3*k)))
k+=1
pi=pi*Decimal(10005).sqrt()/4270934400
pi=pi**(-1)
return pi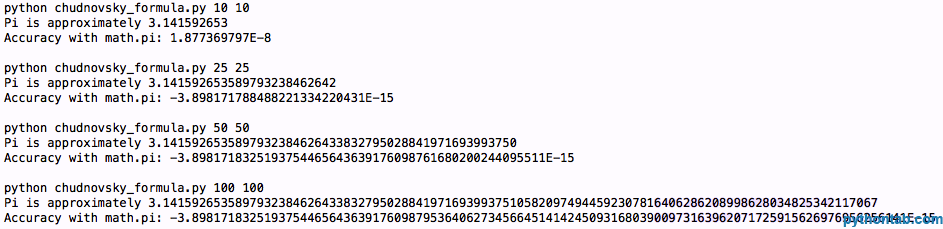
所以我们有了什么结论?花哨的算法不会使机器浮点世界达到更高标准。我真的很期待能有一个比我们用求和公式时所能得到的更好的精度。我猜那是过分的要求。如果你真的需要用PI,就只需使用math.pi变量了。然而,作为乐趣和测试你的计算机真的能有多快,你总是可以尝试第一个计算出Pi的百万位或者更多位是几。