Python で基本的な形態学的フィルタリングを実装する方法-Python チュートリアル-php.cn

Python で基本的な形態学的フィルタリングを実装する方法

PHPz

リリース： 2023-05-21 23:29:36

転載

925 人が閲覧しました

最も基本的な形態学的演算には、腐食、拡張、オープン計算、クローズド計算という 4 つの演算があります。`scipy.ndimage は、バイナリ配列とグレースケール配列に対してこれら 4 つの演算をそれぞれ実装します

##binary_erosionbinary_dilationbinary_closedbinary_openingバイナリ形態

バイナリ	グレースケール
#grey_erosion	腐食
grey_dilation	インフレ
grey_closed	Close (最初に展開してから腐食します)
grey_opening	開く (最初に腐食してから展開します)

いわゆる腐食は、数学記号で次のように表されます。

Python で基本的な形態学的フィルタリングを実装する方法ここで、B

は集合を表します。 B BB の原点が (i, j) にある場合に、B の 1 であるすべての値の合計。この式は、構造 B が A を腐食するために使用されるとき、B の原点が画像 A のピクセル (i,j) に変換されるとき、B が重なり合う領域で完全に囲まれている場合を意味します。 2 つの場合は 1 の値が割り当てられ、それ以外の場合は 0 の値が割り当てられます。 B のある要素が 1 のとき、A の対応する位置も 1 であれば、(i, j) の値は 1 になります。これはより直感的な例です。

拡張はその逆で、

Python で基本的な形態学的フィルタリングを実装する方法 # と表現できます。つまり、B と A の重なり合う領域が重ならない限り、空集合の場合、(i, j) 点を 1 に設定するだけです。

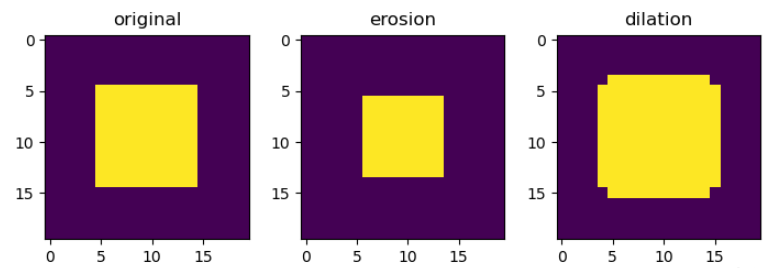
例は次のとおりです

import numpy as np
import matplotlib.pyplot as plt
import scipy.ndimage as sn

x = np.zeros([20,20])
x[5:15, 5:15] = 1
x_ero = sn.binary_erosion(x)
x_dil = sn.binary_dilation(x)

fig = plt.figure()
ax = fig.add_subplot(1,3,1)
ax.imshow(x)
plt.title("original")
ax = fig.add_subplot(1,3,2)
ax.imshow(x_ero)
plt.title("erosion")
ax = fig.add_subplot(1,3,3)
ax.imshow(x_dil)
plt.title("dilation")
plt.show()

ログイン後にコピー

効果は次のとおりです

Python で基本的な形態学的フィルタリングを実装する方法開口操作では、最初に腐食し、次に拡張します。閉じる操作では、最初に拡張してから腐食します。例は次のとおりです。

x = np.zeros([20,20])
x[5:15, 5:15] = 1
x[10:12,10:12] = 0
x[2:4, 2:4] = 1

x_open = sn.binary_opening(x)
x_close = sn.binary_closing(x)

fig = plt.figure()
ax = fig.add_subplot(1,3,1)
ax.imshow(x)
plt.title("original")
ax = fig.add_subplot(1,3,2)
ax.imshow(x_open)
plt.title("opening")
ax = fig.add_subplot(1,3,3)
ax.imshow(x_close)
plt.title("closing")
plt.show()

ログイン後にコピー

結果は次のとおりです。開く操作では孤立した 1 が削除され、閉じる操作では孤立した 1 が削除されることがわかります。 0.

Python で基本的な形態学的フィルタリングを実装する方法グレースケール形態学

グレースケール画像の腐食、拡張、開閉操作は、畳み込みのロジックに同様のものを使用して、そのバイナリ状況を拡張したものです。では、階段画像が

scipy

から直接取得され、侵食、拡張、開閉の操作が順番に実行されます。 <div class="code" style="position:relative; padding:0px; margin:0px;"><pre class="brush:py;">from scipy.misc import ascent img = ascent() funcs = { "original": lambda x, tmp:x, "erosion" : sn.grey_erosion, "dilation" : sn.grey_dilation, "opening" : sn.grey_opening, "closing" : sn.grey_closing } fig = plt.figure() for i, key in enumerate(funcs): ax = fig.add_subplot(2,3,i+1) plt.imshow(funcs[key](img, (10,10)), cmap=plt.cm.gray) plt.title(key) plt.show()</pre><div class="contentsignin">ログイン後にコピー</div></div>

パラメータリスト

バイナリ関数とグレースケール関数のパラメータは同じではありません。以下ではクローズ操作を例にしています。バイナリ関数とグレースケール関数、入力に加えて、両方で共有されるパラメータは次のとおりです。

#構造体は配列型であり、コンボリューションテンプレートとして理解できる構成要素を示します

出力は入力と同じ次元の配列であり、結果を保存できます
#組織フィルタ設定。デフォルトは 0
バイナリ形式フィルタリングを学習するためのその他のパラメータは次のとおりです
```
binary_closing(input, iterations=1, mask=None, border_value=0, brute_force=False)
```
ログイン後にコピー

#iterations は実行回数です

mask マスク配列、bool 型の配列、False に対応する位置は変更されません
border_value エッジの値
#brute_force False の場合、最後の反復のみ変更された値のみが更新されます

grey_closing(input, size=None, footprint=None, mode=&#39;reflect&#39;, cval=0.0)

ログイン後にコピー

size はフィルターテンプレート

モードオプションのリフレクト、定数、ニアレスト、ミラー、ラップ、エッジフィリングメソッド
# #

以上がPython で基本的な形態学的フィルタリングを実装する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。