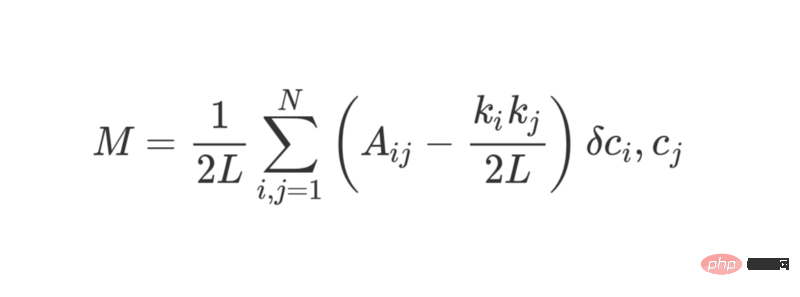データサイエンティストが知っておくべき6つのクラスタリングアルゴリズム

現在、Google ニュースなどの多くのアプリケーションは、主な実装方法としてクラスタリング アルゴリズムを使用しており、大量のラベルなしデータを使用して強力なトピック クラスターを構築できます。この記事では、最も基本的な K 平均法クラスタリングから強力な密度ベースの手法まで 6 種類の主流の手法を紹介しますが、それぞれに専門分野やシナリオがあり、基本的な考え方は必ずしもクラスタリング手法に限定されるものではありません。

#この記事では、シンプルで効率的な K 平均法クラスタリングから始めて、平均シフト クラスタリング、密度ベースのクラスタリング、混合ガウスおよび最大期待値法クラスタリング、階層的クラスタリングを紹介します。構造化データに適用されるグラフ グループ検出。基本的な実装概念を分析するだけでなく、各アルゴリズムの長所と短所も示して実際のアプリケーション シナリオを明確にします。

クラスタリングは、データ ポイントのグループ化を含む機械学習手法です。データ ポイントのセットが与えられると、クラスタリング アルゴリズムを使用して各データ ポイントを特定のグループに分類できます。理論的には、同じグループに属するデータ ポイントは同様のプロパティおよび/または特性を持つはずですが、異なるグループに属するデータ ポイントは非常に異なるプロパティおよび/または特性を持つはずです。クラスタリングは教師なし学習方法であり、多くの分野で一般的に使用される統計データ分析手法です。

K-Means (K-Means) クラスタリング

K-Means は、おそらく最もよく知られたクラスタリング アルゴリズムです。これは、多くのデータ サイエンスおよび機械学習の入門コースの一部です。非常に理解しやすく、コードで実装するのも簡単です。下の写真をご覧ください。

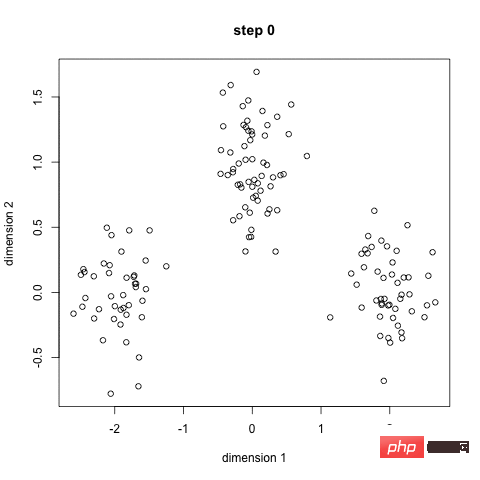
K-Means クラスタリング

まず、いくつかのクラス/グループを選択し、それぞれの中心点をランダムに初期化します。使用するクラスの数を計算するには、データをざっと見て、さまざまなグループを識別してみることをお勧めします。中心点は、各データ点ベクトルと同じ長さの位置であり、上の画像の「X」です。

データ ポイントと各グループの中心の間の距離を計算して各ポイントを分類し、グループの中心に最も近いグループ内の点を分類します。

これらの分類点に基づいて、グループ内のすべてのベクトルの平均を使用してグループの中心を再計算します。

これらの手順を一定回数繰り返すか、各繰り返し後にグループの中心がほとんど変化しないまで繰り返します。グループ センターをランダムに数回初期化し、最良の結果が得られると思われる実行を選択することもできます。

K 平均法の利点は、実際に行っているのは点とグループの中心の間の距離を計算することだけなので、計算が非常に少ないため、高速であることです。したがって、線形複雑さは O(n) になります。

一方、K 平均法にはいくつかの欠点があります。まず、グループ/クラスの数を選択する必要があります。これは常に慎重に行われるわけではありません。クラスタリング アルゴリズムの目的はデータから何らかの洞察を得ることであり、理想的には、分類するクラスの数の問題の解決にクラスタリング アルゴリズムが役立つことが望まれます。 K 平均法は、ランダムに選択されたクラスター中心から開始するため、異なるアルゴリズムでは異なるクラスタリング結果が生成される可能性があります。したがって、結果は再現性がなく、一貫性が欠けている可能性があります。他のクラスタリング方法はより一貫性があります。

K-Medians は、K-Means に関連する別のクラスタリング アルゴリズムです。ただし、平均を使用する代わりに、グループの中央値ベクトルを使用してグループの中心が再計算される点が異なります。この方法は (中央値が使用されるため) 外れ値の影響を受けませんが、中央値ベクトルを計算するときに反復ごとに並べ替えが必要になるため、大きなデータ セットの場合は非常に遅くなります。

平均シフト クラスタリング

平均シフト クラスタリングは、データ ポイントの密集領域を見つけようとするスライディング ウィンドウ ベースのアルゴリズムです。これは重心ベースのアルゴリズムであり、その目的は各グループ/クラスの中心点を見つけることであり、中心点の候補点をスライディング ウィンドウ内の点の平均に更新することによって達成されます。これらの候補ウィンドウは、後処理段階でフィルタリングされてほぼ重複が除去され、中心点とそれに対応するグループの最終セットが形成されます。以下の凡例を参照してください。

単一スライディング ウィンドウの平均シフト クラスタリング

1. 平均シフトを説明するために、上の図に示すように、2 次元空間内の一連の点を考慮します。点 C (ランダムに選択) を中心とし、半径 r のコアを持つ円形のスライディング ウィンドウから始めます。平均シフトは、収束するまで各ステップでより高密度の領域に向かって反復的に移動する山登りアルゴリズムです。
2. 各反復で、スライディング ウィンドウは、中心点をウィンドウ内の点の平均に向かって移動することによって、より高密度の領域に向かって移動します (したがって、この名前が付けられています)。スライディング ウィンドウ内の密度は、その中のポイントの数に比例します。当然のことながら、ウィンドウ内のポイントの平均に向かって移動すると、ポイント密度がより高い領域に向かって徐々に移動します。
3. カーネル内により多くのポイントを収容できる方向がなくなるまで、平均に従ってスライディング ウィンドウを移動し続けます。上の図を見てください。密度が増加しなくなるまで (つまり、ウィンドウ内の点の数が) 円を移動し続けます。
4. ステップ 1 ～ 3 のプロセスは、すべてのポイントが 1 つのウィンドウ内に配置されるまで、多くのスライディング ウィンドウを介して完了します。複数のスライディング ウィンドウが重なる場合、最も多くのポイントを含むウィンドウが保持されます。次に、データ ポイントが配置されているスライディング ウィンドウに基づいてクラスタリングが実行されます。

すべてのスライディング ウィンドウの最初から最後までのプロセス全体を以下に示します。各黒い点はスライディング ウィンドウの重心を表し、各灰色の点はデータ ポイントを表します。

平均シフト クラスタリングの全プロセス

K 平均法クラスタリングと比較して、この方法では平均シフトが一定であるため、クラスターの数を選択する必要がありません。これを自動的に検出します。これは大きな利点です。クラスターの中心が最大点密度に向かってクラスター化するという事実も、自然なデータ駆動型の意味を理解し、それに適応するのが非常に直感的であるため、非常に満足のいくものです。欠点は、ウィンドウ サイズ/半径「r」の選択が重要ではない可能性があることです。

密度ベースのクラスタリング手法 (DBSCAN)

DBSCAN は、平均シフトに似た密度ベースのクラスタリング アルゴリズムですが、いくつかの重要な利点があります。以下の別の楽しいグラフィックをチェックして、始めましょう!

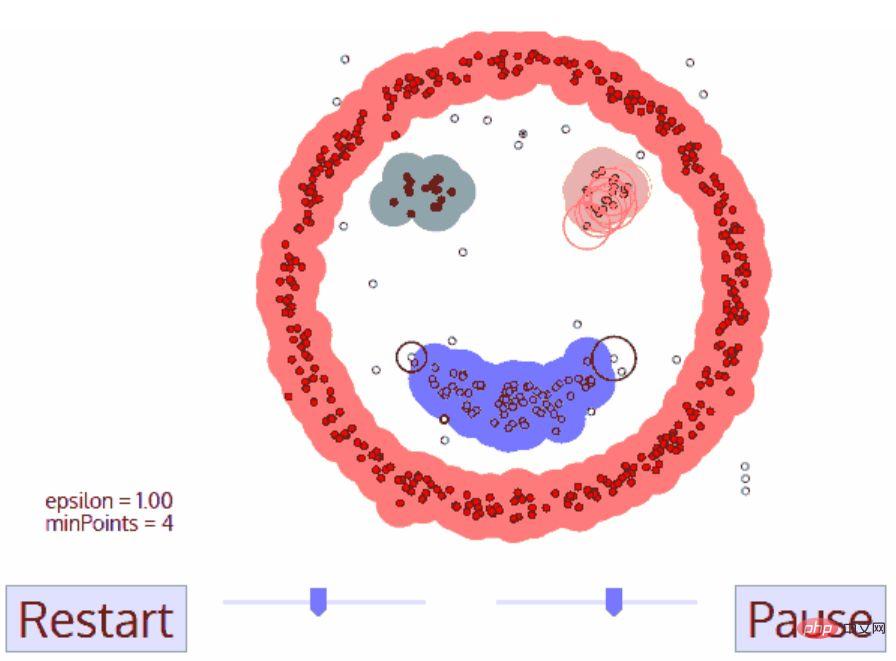
DBSCAN クラスタリング

1. DBSCAN は、まだ訪問されていない任意の開始データ ポイントから開始します。この点の近傍が距離 ε で抽出されます (ε 距離内のすべての点が近傍点です)。
2. この近傍内に十分な数のポイントがある場合 (minPoints による)、クラスタリング プロセスが開始され、現在のデータ ポイントが新しいクラスターの最初のポイントになります。それ以外の場合、ポイントはノイズとしてマークされます (後で、このノイズ ポイントが依然としてクラスターの一部になる可能性があります)。どちらの場合も、ポイントは「訪問済み」としてマークされます。
3. 新しいクラスターの最初の点の場合、ε 距離近傍内の点もクラスターの一部になります。 ε 近傍内のすべての点を同じクラスターに所属させるこのプロセスは、クラスターに追加されたすべての新しい点に対して繰り返されます。
4. クラスター内のすべての点が決定されるまで、つまりクラスターの ε 近傍内のすべての点が訪問されてマークされるまで、ステップ 2 と 3 を繰り返します。
5. 現在のクラスターの処理が完了すると、新しい未訪問のポイントが取得されて処理され、その結果、別のクラスターまたはノイズが発見されます。このプロセスは、すべてのポイントが訪問済みとしてマークされるまで繰り返されます。すべてのポイントが訪問されているため、各ポイントは何らかのクラスターまたはノイズに属します。

DBSCAN には、他のクラスタリング アルゴリズムに比べて多くの利点があります。まず、固定数のクラスターはまったく必要ありません。また、データ ポイントが大きく異なる場合でも、単にデータ ポイントをクラスターにグループ化する平均シフトとは異なり、外れ値をノイズとして識別します。さらに、あらゆるサイズと形状のクラスターを非常によく見つけることができます。

DBSCAN の主な欠点は、クラスターの密度が異なる場合、他のクラスタリング アルゴリズムほどパフォーマンスが低下することです。これは、密度が変化すると、近傍点を特定するために使用される距離のしきい値 ε と minPoints の設定がクラスターごとに変化するためです。この欠点は、距離閾値 ε の推定が再び困難になるため、非常に高次元のデータでも発生します。

混合ガウス モデル (GMM) を使用した予想最大 (EM) クラスタリング

K 平均法の主な欠点は、クラスター中心平均の単純な使用です。以下の図から、これが最良のアプローチではない理由がわかります。左側には、同じ平均値を中心とした異なる半径を持つ 2 つの円形クラスターがあることがはっきりとわかります。これらのクラスターの平均値は非常に近いため、K 平均法ではこの状況に対処できません。 K 平均法は、クラスターが円形でない場合にも失敗します。これもクラスターの中心として平均を使用するためです。

K 平均法の 2 つの失敗例

混合ガウス モデル (GMM) は、K 平均法よりも柔軟性が高くなります。 GMM の場合、データ ポイントはガウス分布であると仮定します。これは、平均を使用してデータ ポイントが円形であると仮定するよりも制限の少ない仮定です。このようにして、クラスターの形状を記述するための 2 つのパラメーター、平均と標準偏差が得られます。 2D を例にとると、これは、クラスターがあらゆる種類の楕円形を取ることができることを意味します (x 方向と y 方向の両方に標準偏差があるため)。したがって、各ガウス分布は単一のクラスターに割り当てられます。

各クラスターのガウス パラメーター (平均や標準偏差など) を見つけるには、Expectation Maximum (EM) と呼ばれる最適化アルゴリズムを使用します。以下の図を見てください。これはクラスターへのガウス近似の例です。その後、GMM を使用して最大期待値クラスタリングのプロセスを続行できます。

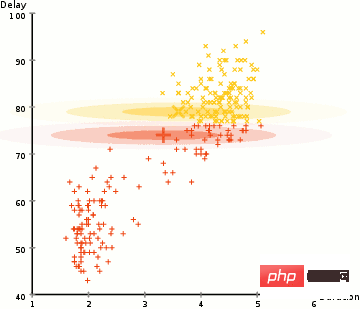
GMM を使用した EM クラスタリング

1. 最初にクラスターの数を選択し (K 平均法によって行われる)、各ガウス分布パラメーターをランダムに初期化します。クラスターの。データをざっと見て、初期パラメータを適切に推測することもできます。ただし、上でわかるように、ガウス分布は最初は非常に貧弱ですが、すぐに最適化されるため、これは 100% 必要というわけではないことに注意してください。
2. 各クラスターのガウス分布を考慮して、各データ ポイントが特定のクラスターに属する確率を計算します。点がガウス分布の中心に近づくほど、その点がそのクラスターに属する可能性が高くなります。ガウス分布では、ほとんどのデータがクラスターの中心に近いと想定されているため、これは直感的に理解できるはずです。
3. これらの確率に基づいて、クラスター内のデータ ポイントの確率を最大化する新しいガウス分布パラメーターのセットを計算します。データ ポイントの位置の加重合計を使用して、これらの新しいパラメーターを計算します。ここで、重みは、データ ポイントがその特定のクラスターに属する確率です。これを視覚的に説明するには、上の画像、特に例として使用する黄色のクラスターを見てみましょう。分布は最初の反復ですぐに始まりますが、黄色の点のほとんどが分布の右側にあることがわかります。確率加重和を計算すると、中心付近に点がいくつかありますが、ほとんどが右側にあります。したがって、分布の平均は当然これらの点に近くなります。また、ほとんどの点が「右上から左下」に分布していることがわかります。したがって、確率の加重合計を最大化するために、標準偏差が変更されて、点によりよく適合する楕円が作成されます。
4. 収束するまでステップ 2 と 3 を繰り返します。収束すると、反復間で分布がほとんど変化しません。

GMM を使用することには 2 つの重要な利点があります。まず、GMM はクラスター共分散の点で K-Means よりも柔軟であり、標準偏差パラメーターにより、クラスターは円に限定されるのではなく、任意の楕円形をとることができます。 K 平均法は実際には GMM の特殊なケースであり、各クラスターの共分散がすべての次元で 0 に近くなります。第 2 に、GMM は確率を使用するため、データ ポイントごとに多数のクラスターが存在する可能性があります。したがって、データ ポイントが 2 つの重なり合うクラスターの中央にある場合、そのデータ ポイントの X パーセントがクラス 1 に属し、Y パーセントがクラス 2 に属すると言うだけで、そのクラスを定義できます。つまり、GMM はハイブリッド資格をサポートします。

凝集型階層クラスタリング

階層クラスタリング アルゴリズムは、実際にはトップダウンまたはボトムアップの 2 つのカテゴリに分類されます。ボトムアップ アルゴリズムでは、まず各データ ポイントを 1 つのクラスターとして扱い、次にすべてのクラスターがすべてのデータ ポイントを含む 1 つのクラスターにマージされるまで、2 つのクラスターを連続してマージ (または集約) します。したがって、ボトムアップ階層クラスタリングは、凝集型階層クラスタリング (HAC) と呼ばれます。このクラスターの階層はツリー (または樹状図) で表されます。ツリーのルートはすべてのサンプルを収集する唯一のクラスターであり、葉は 1 つのサンプルのみを含むクラスターです。アルゴリズムのステップに入る前に、以下の凡例を参照してください。

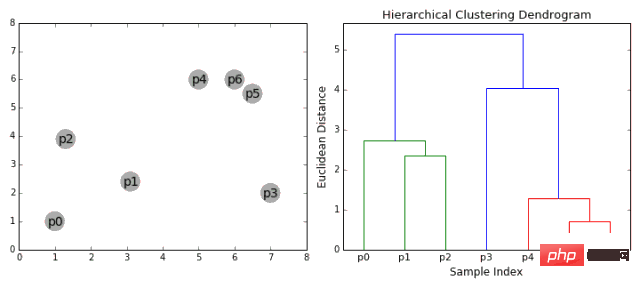
凝集型階層クラスタリング

1. まず、各データ ポイントを単一のクラスターとして扱います。つまり、データ セット内に X データ ポイントがある場合、X 個のクラスターがあります。次に、2 つのクラスター間の距離を測定する距離メトリックを選択します。例として、2 つのクラスター間の距離を、最初のクラスターのデータ ポイントと 2 番目のクラスターのデータ ポイント間の平均距離として定義する平均リンケージを使用します。
2. 各反復で、2 つのクラスターを 1 つにマージします。マージされる 2 つのクラスターの平均リンケージは最小になる必要があります。つまり、選択した距離メトリックによれば、2 つのクラスター間の距離が最小であるため、最も類似しており、マージする必要があります。
3. ツリーのルートに到達するまで、つまりすべてのデータ ポイントを含むクラスターが 1 つだけになるまで、ステップ 2 を繰り返します。このようにして、クラスターのマージをいつ停止するか、つまりツリーの構築をいつ停止するかを選択するだけで、最終的に必要なクラスターの数を選択できます。

階層的クラスタリングでは、クラスターの数を指定する必要はありません。ツリーを構築しているので、最適に見えるクラスターの数を選択することもできます。さらに、このアルゴリズムは距離メトリックの選択に影響されません。他のクラスタリング アルゴリズムでは距離メトリックの選択が重要であるのに対し、それらはすべて同等に良好に実行されます。階層的クラスタリング手法の特に良い例は、基になるデータに階層構造があり、その階層を復元したい場合ですが、他のクラスタリング アルゴリズムではこれを行うことができません。 K-Means や GMM の線形複雑さとは異なり、階層クラスタリングのこれらの利点は、時間計算量が O(n³) であるため、効率が低下するという犠牲を伴います。

グラフ コミュニティ検出

データがネットワークまたはグラフ (グラフ) として表現できる場合、グラフ コミュニティ検出方法を使用してクラスタリングを完了できます。このアルゴリズムでは、グラフ コミュニティは通常、ネットワークの他の部分よりも密接に接続された頂点のサブセットとして定義されます。

おそらく最も直感的なケースはソーシャル ネットワークです。頂点は人を表し、頂点を接続するエッジは友人やファンであるユーザーを表します。ただし、システムをネットワークとしてモデル化するには、さまざまなコンポーネントを効率的に接続する方法を見つける必要があります。クラスタリングのためのグラフ理論の革新的なアプリケーションには、画像データの特徴抽出、遺伝子制御ネットワークの分析などが含まれます。

以下は、Wikipedia ページからのリンクに基づいて接続された、最近閲覧した 8 つの Web サイトを示す簡単な図です。

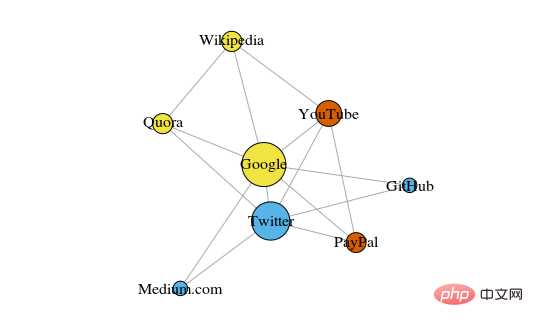
これらの頂点の色はグループ関係を示し、サイズは中心性に基づいて決定されます。これらのクラスターは実生活でも意味を持ちます。黄色の頂点は通常、参照/検索サイトであり、青色の頂点はすべてオンライン公開サイト (記事、ツイート、またはコード) です。

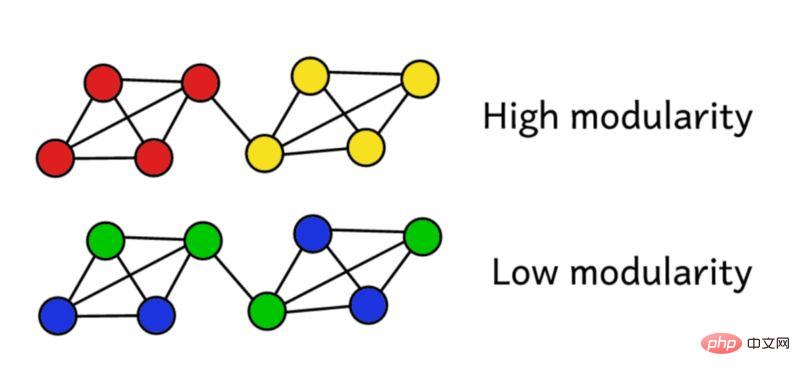
ネットワークをグループにクラスタ化したとします。このモジュール性スコアを使用して、クラスタリングの品質を評価できます。スコアが高いほど、ネットワークが「正確な」グループにセグメント化されたことを意味し、スコアが低いほど、クラスタリングがランダムに近いことを意味します。以下の図に示すように:

モジュール性は次の式を使用して計算できます:

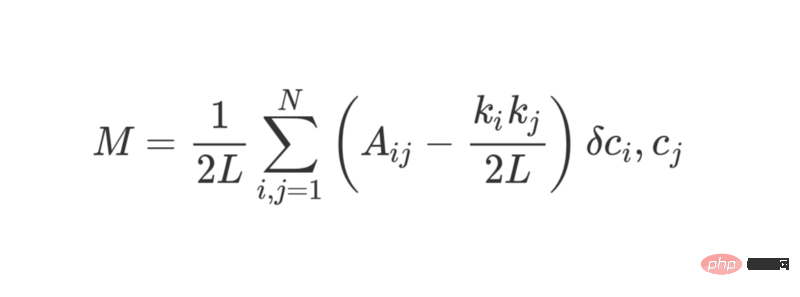
ここで、L はネットワーク内のエッジ 量 k_i と k_j は各頂点の次数を指し、各行と列の項を合計することで見つけることができます。 2 を乗算し、2L で割ることは、ネットワークがランダムに割り当てられた場合の頂点 i と j の間のエッジの予想数を表します。

全体として、括弧内の用語は、ネットワークの実際の構造と、ランダムに組み合わせた場合の予想される構造との違いを表します。その値を調べると、A_ij = 1 かつ ( k_i k_j ) / 2L が小さいときに最大値を返すことがわかります。これは、固定点 i と j の間に「予期しない」エッジがある場合、結果の値が大きくなるということを意味します。

最後のδc_i、c_jは有名なクロネッカーδ関数(クロネッカーデルタ関数)です。 Python の説明は次のとおりです:

グラフのモジュール性は上記の式で計算でき、モジュール性が高いほど、ネットワークがさまざまなグループにクラスター化される度合いが高くなります。したがって、ネットワークをクラスタ化する最適な方法は、最適化手法を通じて最大限のモジュール性を探すことによって見つけることができます。

組み合わせ論によれば、頂点が 8 つしかないネットワークの場合、4,140 の異なるクラスタリング方法があることがわかります。 16 頂点のネットワークは 100 億通り以上にクラスタ化されます。 32 個の頂点を持つネットワークで可能なクラスタリング手法は 128 セプティリオン (10^21) を超えます。ネットワークに 80 個の頂点がある場合、可能なクラスタリング手法の数は、観測可能な宇宙のクラスタリング手法の数を超えています。

したがって、あらゆる可能性を試すことなく、最高のモジュール性スコアをもたらすクラスターの評価にうまく機能するヒューリスティックに頼らなければなりません。これは、Fast-Greedy Modularity-Maximization と呼ばれるアルゴリズムで、上記の凝集型階層クラスタリング アルゴリズムに似ています。 Mod-Max は距離に基づいてグループを融合するのではなく、モジュール性の変化に基づいてグループを融合するだけです。

その仕組みは次のとおりです:

• まず最初に各頂点を独自のグループに割り当て、次にネットワーク全体のモジュール性 M を計算します。
• ステップ 1 では、各コミュニティ ペアが少なくとも 1 つの片側リンクによってリンクされていることが必要です。2 つのコミュニティが結合した場合、アルゴリズムは結果として生じるモジュール性の変化 ΔM を計算します。
• 2 番目のステップは、ΔM の増加が最も大きいグループのペアを選択し、それらを結合することです。次に、このクラスターに対して新しいモジュール性 M が計算され、記録されます。
• ステップ 1 と 2 を繰り返し、そのたびにグループ ペアを融合して、最終的に ΔM の最大ゲインが得られ、新しいクラスタリング パターンとそれに対応するモジュール性スコア M を記録します。
• すべての頂点が巨大なクラスターにグループ化されたら停止できます。次に、アルゴリズムはこのプロセスでレコードを検査し、最も高い M 値が返されたクラスタリング パターンを見つけます。これは返されたグループ構造です。

コミュニティ検出は、グラフ理論の人気のある研究分野です。その限界は主に、いくつかの小さなクラスターが無視され、構造化グラフ モデルにのみ適用できるという事実に反映されています。ただし、このタイプのアルゴリズムは、一般的な構造化データや実際のネットワーク データでは非常に優れたパフォーマンスを発揮します。

結論

上記は、データ サイエンティストが知っておくべき 6 つの主要なクラスタリング アルゴリズムです。この記事は、さまざまなアルゴリズムの視覚化を示して終了します。

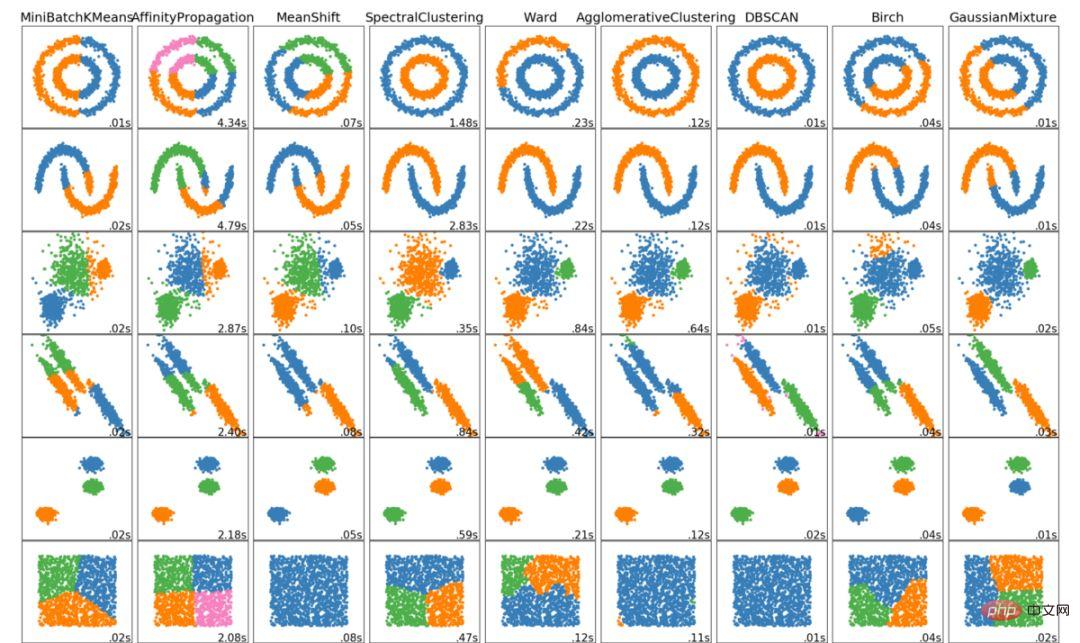
以上がデータサイエンティストが知っておくべき6つのクラスタリングアルゴリズムの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。