二分木の確立と走査について、この記事では詳細に紹介し、事前二分木走査、順序二分木走査、事後二分木走査のアルゴリズムについても説明します。コードは次のとおりです。誰でもわかるように引用します。理解しやすいように、この記事の導入は二分木と二分探索木から始める必要があります。 apache php mysql

二分木と二分探索木

js_前順、中順、後順での二分木走査のための3つのアルゴリズム_単純な二分木の実装

ツリーに関する関連用語:

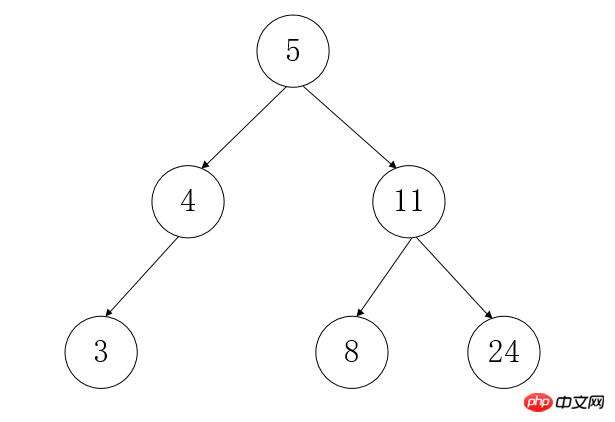
ノード: ツリー内の各要素をノードと呼びます。

ルートノード: 全体の頂点に位置するノードツリー、上の図 5 に示すように、親ノードがありません

子ノード: 他のノードの子孫

リーフノード: 図 3 8 24 に示すように、子ノードのない要素はリーフノードと呼ばれます

バイナリツリー: バイナリツリーはデータ構造であり、その組織関係は自然界の木のようなものです。公式言語での定義は次のとおりです。これは、空であるか、ルートと呼ばれる要素と、それぞれ左サブツリーおよび右サブツリーと呼ばれる 2 つの素のバイナリツリーで構成される有限要素のセットです。

二分探索ツリー:
二分探索ツリーは二分探索ツリー (BST) とも呼ばれ、左側のノードには親ノードよりも小さい値を、右側のノードには親ノードよりも大きい値のみを格納できます。上の図は二分探索木を示しています。

コードの実装

まず、二分探索ツリーを表すクラスを作成します。その中にノードを作成するための Node クラスが必要です

    function BinarySearchTree () {
        var Node = function(key) {
            this.key = key,
            this.left = null,
            this.right = null
        }
        var root = null
    }

ログイン後にコピー

いくつかのメソッドも必要です:

insert(key) 新しいキーを挿入します。
inOrderTraverse() はツリーの順序トラバーサルを実行し、結果を出力します
preOrderTraverse() はツリーの前順序トラバースを実行し、結果を出力します
postOrderTraverse() は事後順序トラバーサルを実行しますツリーの値を取得し、結果を出力します
search(key) はツリー内のキーを検索し、存在する場合は true を返し、存在しない場合は false を返します
findMin() は、キーの最小値を返しますTree
findMax() はツリーを返します
remove(key) の最大値はツリー内のキーを削除します

はツリーにキーを挿入します

はツリーに新しいキーを挿入しますホームページでは、新しいノードの Class インスタンスを表す Node を作成する必要があるため、Node クラスを新規作成し、挿入する必要があるキー値を渡す必要があります。これにより、左右のノードが null の新しいノードに自動的に初期化されます。まず、ツリーが空であるかどうかを判断する必要があります。空でない場合は、補助メソッドの insertNode() メソッドを呼び出します。ルートノードと新しいノードを

    this.insert = function(key) {
        var newNode = new Node(key)
        if(root === null) {
            root = newNode
        } else {
            insertNode(root, newNode)
        }
    }

ログイン後にコピー

に追加します

    var insertNode = function(node, newNode) {
        if (newNode.key <= node.key) {
            if (node.left === null) {
                node.left = newNode
            }else {
                insertNode(node.left, newNode)
            }
        }else {
            if (node.right === null) {
                node.right = newNode
            }else {
                insertNode(node.right, newNode)
            }
        }
    }

ログイン後にコピー

insertNode()メソッドを定義します。このメソッドはそれ自体を再帰的に呼び出して、新しく追加されたノードの適切な位置を見つけます

    this.inOrderTraverse = function() {
        inOrderTraverseNode(root)
    }

ログイン後にコピー

インオーダートラバーサルメソッドを完了します

順序トラバーサルには、各ノードをトラバースするために再帰的に自身を呼び出すことができる inOrderTraverseNode(node) メソッドが必要です

    var inOrderTraverseNode = function(node) {
        if (node !== null) {
            inOrderTraverseNode(node.left)
            console.log(node.key)
            inOrderTraverseNode(node.right)
        }
    }

ログイン後にコピー

このメソッドは、各ノードのキー値を出力するには、再帰的な終了条件が必要です - 受信ノードが null かどうかを確認しますそうでない場合は、再帰的に自分自身を呼び出してノードの左右のノードを確認します。これも非常に簡単に実装できます。、わずかな変更で、事前順序トラバーサルと事後順序トラバーサルを実現できます

上記のコード:

このようにして、ツリー全体をトラバースすることができます。ツリーは順番にトラバースされます

    // 实现先序遍历
    this.preOrderTraverse = function() {
        preOrderTraverseNode(root)
    }
    var preOrderTraverseNode = function(node) {
        if (node !== null) {
            console.log(node.key)
            preOrderTraverseNode(node.left)
            preOrderTraverseNode(node.right)
        }
    }

    // 实现后序遍历
    this.postOrderTraverse = function() {
        postOrderTraverseNode(root)
    }
    var postOrderTraverseNode = function(node) {
        if (node !== null) {
            postOrderTraverseNode(node.left)
            postOrderTraverseNode(node.right)
            console.log(node.key)
        }
    }

ログイン後にコピー

実際、内部ステートメントは前後の位置を変更しています。これは、事前順序トラバーサル (ルート-左-右)、順序トラバーサル (左-ルート-右)、順序トラバーサルの 3 つのトラバーサルルールに準拠しているだけです。 (left-right-root)

最初にテストをしてみましょう

完全なコードは次のとおりです:

    function BinarySearchTree () {
        var Node = function(key) {
            this.key = key,
            this.left = null,
            this.right = null
        }
        var root = null
        
        //插入节点
        this.insert = function(key) {
            var newNode = new Node(key)
            if(root === null) {
                root = newNode
            } else {
                insertNode(root, newNode)
            }
        }
        var insertNode = function(node, newNode) {
            if (newNode.key <= node.key) {
                if (node.left === null) {
                    node.left = newNode
                }else {
                    insertNode(node.left, newNode)
                }
            }else {
                if (node.right === null) {
                    node.right = newNode
                }else {
                    insertNode(node.right, newNode)
                }
            }
        } 
        
        //实现中序遍历
        this.inOrderTraverse = function() {
            inOrderTraverseNode(root)
        }
        var inOrderTraverseNode = function(node) {
            if (node !== null) {
                inOrderTraverseNode(node.left)
                console.log(node.key)
                inOrderTraverseNode(node.right)
            }
        }
        // 实现先序遍历
        this.preOrderTraverse = function() {
            preOrderTraverseNode(root)
        }
        var preOrderTraverseNode = function(node) {
            if (node !== null) {
                console.log(node.key)
                preOrderTraverseNode(node.left)
                preOrderTraverseNode(node.right)
            }
        }

        // 实现后序遍历
        this.postOrderTraverse = function() {
            postOrderTraverseNode(root)
        }
        var postOrderTraverseNode = function(node) {
            if (node !== null) {
                postOrderTraverseNode(node.left)
                postOrderTraverseNode(node.right)
                console.log(node.key)
            }
        }
    }

ログイン後にコピー

は新しいノードを追加して走査するメソッドを実際に完了しました。テストしてみましょう:

いくつかの要素を含む配列を定義しますその中の要素

var arr = [9,6,3,8,12,15]

ログイン後にコピー

arr の各要素を二分探索ツリーに適宜挿入し、結果を出力します

    var tree = new BinarySearchTree()
    arr.map(item => {
        tree.insert(item)
    })
    tree.inOrderTraverse()
    tree.preOrderTraverse()
    tree.postOrderTraverse()

ログイン後にコピー

コードを実行したら、まずノードを挿入した後の全体の構造を見てみましょうツリーの状況:

出力結果

In-order traversal:

<p>3<img src="https://img.php.cn//upload/image/461/709/758/1533281913515198.png" title="1533281913515198.png" alt="js_前順、中順、後順での二分木走査のための3つのアルゴリズム_単純な二分木の実装"/>6</p>8<p>9</p>12<p>15<code><br/>3<br/>6<br/>8<br/>9<br/>12<br/>15<br/>

先序遍历： 9 6 3 8 12 15 

后序遍历： 3 8 6 15 12 9 

Pre-order traversal: 9<h2> 6</h2> 381215🎜🎜Postorder traversal: 🎜3🎜8🎜6🎜15🎜12🎜9🎜🎜🎜明らかに、結果は期待どおりなので、次を使用します上記の JavaScript コードは、ツリーへのノードの挿入と 3 つのトラバーサルメソッドを実装しています。同時に、二分探索ツリーでは、左端のノードの値が最も小さく、右端のノードの値が最大であることがわかります。 , したがって、二分探索木は最大値と最小値を簡単に取得できます🎜🎜最小値と最大値を見つけるにはどうすればよいですか🎜🎜?実際には、ルートノードを minNode/または maxNode メソッドに渡し、ループを通じて左側 (minNode)/右側 (maxNode) のノードが null であることを判断するだけです🎜🎜 実装コード: 🎜

    // 查找最小值
    this.findMin = function() {
        return minNode(root)
    }
    var minNode = function(node) {
        if (node) {
            while (node && node.left !== null) {
                node = node.left
            }
            return node.key
        }
        return null
    }
    
    // 查找最大值
    this.findMax = function() {
        return maxNode(root)
    }
    var maxNode = function (node) {
        if(node) {
            while (node && node.right !== null) {
                node =node.right
            }
            return node.key
        }
        return null
    }

ログイン後にコピー

所搜特定值

this.search = function(key) {
    return searchNode(root, key)
}

ログイン後にコピー

同样，实现它需要定义一个辅助方法,这个方法首先会检验node的合法性，如果为null，直接退出，并返回fasle。如果传入的key比当前传入node的key值小，它会继续递归查找node的左侧节点，反之，查找右侧节点。如果找到相等节点，直接退出，并返回true

    var searchNode = function(node, key) {
        if (node === null) {
            return false
        }
        if (key < node.key) {
            return searchNode(node.left, key)
        }else if (key > node.key) {
            return searchNode(node.right, key)
        }else {
            return true
        }
    }

ログイン後にコピー

移除节点

移除节点的实现情况比较复杂，它会有三种不同的情况：

需要移除的节点是一个叶子节点
需要移除的节点包含一个子节点
需要移除的节点包含两个子节点

和实现搜索指定节点一元，要移除某个节点，必须先找到它所在的位置，因此移除方法的实现中部分代码和上面相同：

    // 移除节点
    this.remove = function(key) {
        removeNode(root,key)
    }
    var removeNode = function(node, key) {
        if (node === null) {
            return null
        }
        if (key < node.key) {
            node.left = removeNode(node.left, key)
            return node
        }else if(key > node.key) {
            node.right = removeNode(node.right,key)
            return node
        }else{
            //需要移除的节点是一个叶子节点
            if (node.left === null && node.right === null) {
                node = null
                return node
            }
            //需要移除的节点包含一个子节点
            if (node.letf === null) {
                node = node.right
                return node
            }else if (node.right === null) {
                node = node.left
                return node
            }
            //需要移除的节点包含两个子节点
            var aux = findMinNode(node.right)
            node.key = aux.key
            node.right = removeNode(node.right, axu.key)
            return node
        }
    }
    var findMinNode = function(node) {
        if (node) {
            while (node && node.left !== null) {
                node = node.left
            }
            return node
        }
        return null
    }

ログイン後にコピー

其中，移除包含两个子节点的节点是最复杂的情况，它包含左侧节点和右侧节点，对它进行移除主要需要三个步骤：

需要找到它右侧子树中的最小节点来代替它的位置
将它右侧子树中的最小节点移除
将更新后的节点的引用指向原节点的父节点

有点绕儿，但必须这样，因为删除元素后的二叉搜索树必须保持它的排序性质

测试删除节点

tree.remove(8)
tree.inOrderTraverse()

ログイン後にコピー

打印结果：

3 6 9 12 15 

8 这个节点被成功删除了，但是对二叉查找树进行中序遍历依然是保持排序性质的

到这里，一个简单的二叉查找树就基本上完成了，我们为它实现了，添加、查找、删除以及先中后三种遍历方法

存在的问题

但是实际上这样的二叉查找树是存在一些问题的，当我们不断的添加更大/更小的元素的时候，会出现如下情况：

tree.insert(16)
tree.insert(17)
tree.insert(18)

ログイン後にコピー

来看看现在整颗树的情况：

js_前順、中順、後順での二分木走査のための3つのアルゴリズム_単純な二分木の実装

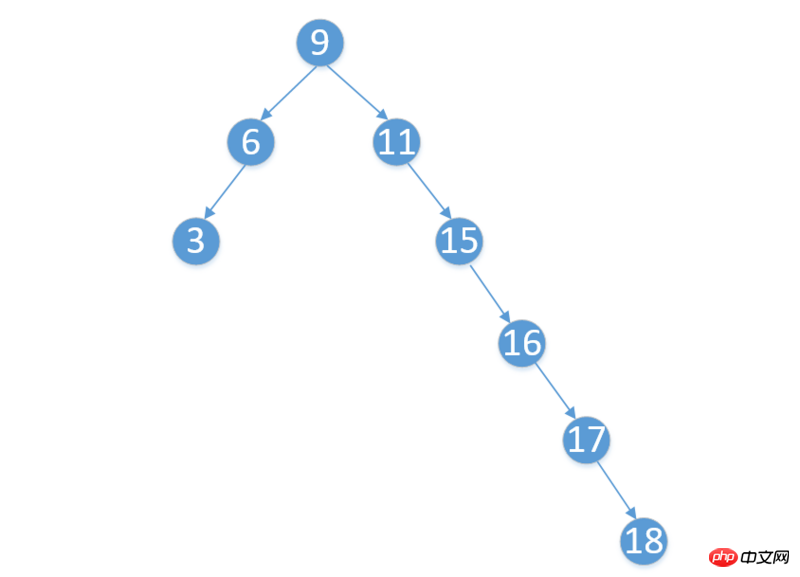
看图片容易得出它是不平衡的，这又会引出平衡树的概念，要解决这个问题，还需要更复杂的实现，例如：AVL树，红黑树哎，之后再慢慢去学习吧

二叉树遍历算法-php的示例

二叉树的中序遍历,该怎么解决

以上がjs_前順、中順、後順での二分木走査のための3つのアルゴリズム_単純な二分木の実装の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。