
この記事の内容は、分類評価指標と回帰評価指標の詳細な説明と、Python コードの実装です。必要な友人に参照してください。
パフォーマンス測定 (評価) 指標は主に 2 つのカテゴリに分類されます:
1) 分類評価指標 (分類)、主に分析、離散、整数。具体的な指標としては、アキュラシー(精度)、プレシジョン(精度)、リコール(再現率)、F値、P-Rカーブ、ROCカーブ、AUCなどが挙げられます。
2) 回帰評価指標(回帰)は、主に整数と実数の関係を分析します。その特定の指標には、説明分散スコア (explianed_variance_score)、平均絶対誤差 MAE (mean_absolute_error)、平均二乗誤差 MSE (mean-squared_error)、二乗平均平方根差 RMSE、クロス エントロピー損失 (対数損失、クロスエントロピー損失)、R 二乗が含まれます。値(決定係数、r2_score)。
通常、関心のあるカテゴリはポジティブなカテゴリであり、他のカテゴリはネガティブなカテゴリであると仮定します (したがって、複数クラスの問題も 2 つに要約できます)。カテゴリー)
混同行列は次のとおりです
| 実際のカテゴリ | 予測カテゴリ | |||
| ポジティブ | ネガティブ | 概要 | ||
| ポジティブ | TP | FN | 表内の P (実際は正) | |
| 負 | FP | TN | N (実際は負) | |
表内のモード: 最初のものは、予測結果が正しいか間違っているか、2 番目は予測されたカテゴリを表します。たとえば、TP は True Positive (正しい予測が陽性クラスであること) を意味し、FN は False Negative (誤った予測が陰性クラスであること) を意味します。
| Measurement | Accuracy (精度) | Precision (精度) | 再現率(リコール) | F値 |
| 定義 | サンプル総数に対する正しく分類されたサンプル数の比率(スパムであると予測される実際のスパムテキストメッセージの割合) | 決定as 陽性例の数に対する真陽性例の数の比率 (正しく分類され、検出されたすべての実際のスパム テキスト メッセージの割合) | 陽性例の総数に対する真陽性例の数の比率 | 正解率調和平均F-スコア |
| 、再現率付き | 精度=
| 精度=
|
リコール =
|
F - スコア =
|
1. 適合率は適合率とも呼ばれ、再現率は再現率とも呼ばれます
2. より一般的に使用されるのは F1、
python3.6 コード実装:
#调用sklearn库中的指标求解from sklearn import metricsfrom sklearn.metrics import precision_recall_curvefrom sklearn.metrics import average_precision_scorefrom sklearn.metrics import accuracy_score#给出分类结果y_pred = [0, 1, 0, 0]
y_true = [0, 1, 1, 1]
print("accuracy_score:", accuracy_score(y_true, y_pred))
print("precision_score:", metrics.precision_score(y_true, y_pred))
print("recall_score:", metrics.recall_score(y_true, y_pred))
print("f1_score:", metrics.f1_score(y_true, y_pred))
print("f0.5_score:", metrics.fbeta_score(y_true, y_pred, beta=0.5))
print("f2_score:", metrics.fbeta_score(y_true, y_pred, beta=2.0))1) P-R曲線
手順:
1. 「スコア」値を高いものから低いものまで並べ替え、それらをしきい値として順番に使用します。
2. 各しきい値について、このしきい値以上の「スコア」値を持つサンプルをテストします。はポジティブな例であり、その他はネガティブな例です。したがって、一連の予測数値が形成されます。
例: 0.9を閾値として設定すると、最初のテストサンプルが陽性例となり、2、3、4、5が陰性例となります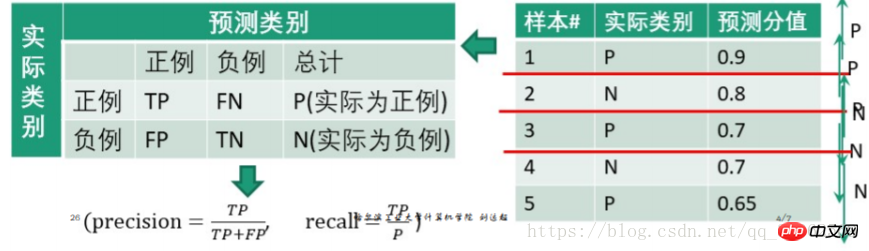
陰性であると予測される例 | 合計 | 陽性の場合(スコアが閾値より大きい) | |
| 0.1 | 1 | 陰性の場合(スコアが閾値より小さい) | |
| 0.8+0.7+0.7+0.65 = 2.85 | 4 | 精度= | |
再現率=
| |||
2) ROC 曲線#precision和recall的求法如上 #主要介绍一下python画图的库 import matplotlib.pyplot ad plt #主要用于矩阵运算的库 import numpy as np#导入iris数据及训练见前一博文 ... #加入800个噪声特征,增加图像的复杂度 #将150*800的噪声特征矩阵与150*4的鸢尾花数据集列合并 X = np.c_[X, np.random.RandomState(0).randn(n_samples, 200*n_features)] #计算precision,recall得到数组 for i in range(n_classes): #计算三类鸢尾花的评价指标, _作为临时的名称使用 precision[i], recall[i], _ = precision_recall_curve(y_test[:, i], y_score[:,i])#plot作图plt.clf() for i in range(n_classes): plt.plot(recall[i], precision[i]) plt.xlim([0.0, 1.0]) plt.ylim([0.0, 1.05]) plt.xlabel("Recall") plt.ylabel("Precision") plt.show()ログイン後にコピー上記のコードを完了すると、アヤメの花データセットの P-R 曲線が得られます
横軸: 偽陽性率 fp rate = FP/N
縦軸: True陽性率 tp rate = TP / N 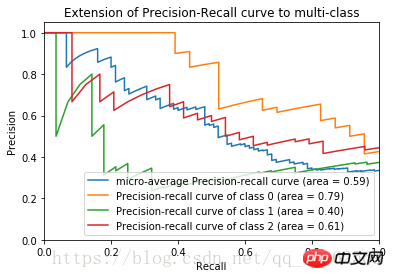 手順:
手順:
1. 「スコア」値を高いものから低いものまで並べ替え、それらを順番にしきい値として使用します
2. 各しきい値について、より大きい「スコア」値を持つサンプルをテストします。このしきい値以上は正の例とみなされ、それ以外は負の例とみなされます。したがって、一連の予測数値が形成されます。
P-R曲線の計算と似ているので詳細は割愛します
アイリスの花データセットの ROC 画像は
2) 平均絶対誤差 MAE (Mean Absolute error)AUC (Area Under Curve) は、ROC 曲線の下の面積として定義されます
1) 解釈可能な分散スコア
AUC 値は、分類器の全体的な数値を提供します。通常、AUC が大きいほど優れた分類器であり、その値は [0, 1]
2.2. 回帰評価指標
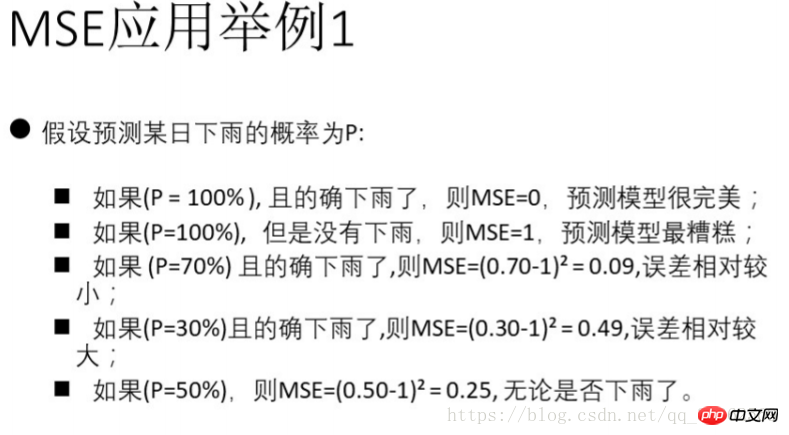
 3) MSE (平均二乗誤差)
3) MSE (平均二乗誤差) 
4) ロジスティック回帰損失 
 5) 一貫性評価 - ピアソン相関係数法
5) 一貫性評価 - ピアソン相関係数法  Python コード実装
Python コード実装
from sklearn.metrics import log_loss log_loss(y_true, y_pred)from scipy.stats import pearsonr pearsonr(rater1, rater2)from sklearn.metrics import cohen_kappa_score cohen_kappa_score(rater1, rater2)
以上が分類評価指標と回帰評価指標とPythonコードの実装について詳しく解説の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。