AVLツリーJava-＆＃＆チュートリアル-php.cn

AVLツリーJava

王林

リリース： 2024-08-30 16:17:11

オリジナル

537 人が閲覧しました

AVL ツリーは、自己平衡型バイナリツリーとしても知られており、左右のサブツリーのそれぞれの高さの差を平衡化して計算するために使用され、結果は平衡化されたツリー全体で複数になることはありません。 Binary Search ツリー操作では、AVL ツリーの一部としても必要な挿入、削除、検索、最大値、最小値の操作が可能です。これらすべての操作はコストがかかる作業であると考えられており、すべての BST の高さの差が維持されれば、それに関連するコストと時間の複雑さを維持できます。

無料ソフトウェア開発コースを始めましょう

Web 開発、プログラミング言語、ソフトウェアテスト、その他

構文:

そのような適切な構文はありませんが、Java で実装する場合、AVL ツリーは構文が次のように表されるデータ構造とみなされます。

Class Node_demo
{
int key, height_0;
Node left, right;
Node_demo (int d_1)
{
key = d_1;
height_0 = 1;
}
}
class AVLTree_demo1 {
Node root_0;
int height_0(Node N_1) {
if (N_1== null)
return 0;
return N_1.height;
}

ログイン後にコピー

説明:

ここの構文フローでは、クラス Node_demo にキー、高さ、要素が格納されるキーと値のペアを記述する構造体が含まれています。これに、ルートノードとその関連要素を含む AVL_Tree デモ_1 ノードが続きます。値のペアは、値が null でどこでも維持される高さを持ちます。

AVL ツリーは Java でどのように機能しますか?

AVL ツリーが Java で動作する適切なフローが存在し、1962 年に GM Adelson によって発明されました。
AVL ツリーは、高さバランスのとれた二分探索ツリーとして定義されます。各ノードは、左側のサブツリーの高さから右側のサブツリーの高さを減算することによって計算されるバランス係数に関連付けられます。
バランス係数が -1 から 1 の間にある場合、ツリーはバランスが取れていると呼ばれます。それ以外の場合、ツリーは上から下までバランスをとる必要があります。
バランスツリーが二分探索木の高さを制御するため、高さは O(h) になりますが、二分探索木が歪んだ場合はそれよりも拡張する必要があるという規定があります。操作すると (n-1) になります。
一度歪んだツリーが制限されると、その場合、O (log n) (n はノード数) として出力されるすべての操作に上限が課されます。
AVL ツリーを回転する方法もありますが、これはバランス係数が -1、1、または 0 の間にある 1 つの条件でのみ発生します。
回転には次の 4 種類があります:
LL 回転: ノードがノード D を持つツリーの左側のサブツリーにある場合、ノードが挿入されます。
RR Rotations: ノードがノード D を持つツリーの右側のサブツリーにある場合、ノードが挿入されます。
LR 回転: ノード D を持つ左側のサブツリーの右側のサブツリーにノードが挿入される場合、ノードが挿入されます。
RL ローテーション: ノード D を持つ右のサブツリーの左のサブツリーにノードが挿入される場合、ノードが挿入されます。

ここで、D は、高さとバランス係数が -1、1、および 0 以外にあるノードを表します。そのため、これらすべての回転が適切な形式に作成するために必要となります。

多くの操作が存在するため、操作には適切な分析を伴う適切なローテーションが必要です。

例: この例では、以下の出力に示すように、挿入、前順序、後順序、およびレベル順序表現を使用した左挿入と右挿入が行われる AVL ツリーを示します。

import java. util.LinkedList;
import java.util.Queue;
class Node_8 {
int data_0, height_1;
Node_8 left_nd_0;
Node_8 right_nd_0;
Node_8(int d_2) {
data_0 = d_2;
height_1 = 1;
}
}
public class AVLTree_Demo
{
Node_8 root_0;
int height_1(Node_8 N) {
if (N == null)
return 0;
return N.height_1;
}
int max_2(int a_0,  int b_0) {
return (a_0 > b_0) ? a_0 : b_0;
}
Node_8 rightRotation_mode(Node_8 oldRoot_0) {
Node_8 newRoot_0 = oldRoot_0.left_nd_0;
Node_8 temp_0 = newRoot_0.right_nd_0;
newRoot_0.right_nd_0 = oldRoot_0;
oldRoot_0.left_nd_0 = temp_0;
newRoot_0.height_1 = max_2(height_1(newRoot_0.left_nd_0), height_1(newRoot_0.right_nd_0)) + 1;
oldRoot_0.height_1 = max_2(height_1(oldRoot_0.left_nd_0), height_1(oldRoot_0.right_nd_0)) + 1;
return newRoot_0;
}
Node_8 leftRotation_mode(Node_8 oldRoot_0) {
Node_8 newRoot_0 = oldRoot_0.right_nd_0;
Node_8 temp_0 = newRoot_0.left_nd_0;
newRoot_0.left_nd_0 = oldRoot_0;
oldRoot_0.right_nd_0 = temp_0;
newRoot_0.height_1 = max_2(height_1(newRoot_0.left_nd_0), height_1(newRoot_0.right_nd_0)) + 1;
oldRoot_0.height_1=max_2(height_1(oldRoot_0.left_nd_0), height_1(oldRoot_0.right_nd_0)) + 1;
return newRoot_0;
}
int balFactor_c(Node_8 root_0) {
if(root_0 == null)
return 0;
return height_1(root_0.left_nd_0) - height_1(root_0.right_nd_0);
}
Node_8 insert(Node_8 root_0, int data_0) {
if(root_0 == null)
return new Node_8(data_0);
else if(data_0 < root_0.data_0)
root_0.left_nd_0 = insert(root_0.left_nd_0, data_0);
else if(data_0 > root_0.data_0)
root_0.right_nd_0 = insert(root_0.right_nd_0, data_0);
else
return root_0;
root_0.height_1= max_2(height_1(root_0.left_nd_0), height_1(root_0.right_nd_0)) + 1;
int bal = balFactor_c(root_0);
if(bal > 1 && data_0 < root_0.left_nd_0.data_0)
return rightRotation_mode(root_0);
if(bal < -1 && data_0 > root_0.right_nd_0.data_0)
return leftRotation_mode(root_0);
if(bal > 1 && data_0 > root_0.left_nd_0.data_0) {
root_0.left_nd_0 = leftRotation_mode(root_0.left_nd_0);
return rightRotation_mode(root_0);
}
if(bal < -1 && data_0 < root_0.right_nd_0.data_0) {
root_0.right_nd_0 = rightRotation_mode(root_0.right_nd_0);
return leftRotation_mode(root_0);
}
return root_0;
}
void preOrder_traversal(Node_8 node) {
if (node != null) {
System.out.print(node.data_0 + " ");
preOrder_traversal(node.left_nd_0);
preOrder_traversal(node.right_nd_0);
}
}
void levelOrder_traversal(Node_8 root) {
Queue<Node_8> q_1 = new LinkedList<Node_8>();
q_1.add(root);
while(!q_1.isEmpty()) {
Node_8 current = q_1.peek();
System.out.print(current.data_0 + " ");
if(current.left_nd_0 != null)
q_1.add(current.left_nd_0);
if(current.right_nd_0 != null)
q_1.add(current.right_nd_0);
q_1.poll();
}
}
public static void main (String args[]) {
AVLTree_Demo tree = new AVLTree_Demo ();
tree. root_0 = tree.insert(tree.root_0, 15);
tree.root_0 = tree.insert(tree.root_0, 20);
tree.root_0 = tree.insert(tree.root_0, 19);
tree.root_0 = tree.insert(tree.root_0, 40);
tree.root_0 = tree.insert(tree.root_0, 50);
tree.root_0 = tree.insert(tree.root_0, 25);
System.out.println("order_of_Preorder_traversal_representation : ");
tree.preOrder_traversal(tree.root_0);
System.out.println();
System.out.println("Levelorder_of_traversal_representation : ");
tree.levelOrder_traversal(tree.root_0);
}
}

ログイン後にコピー

出力:

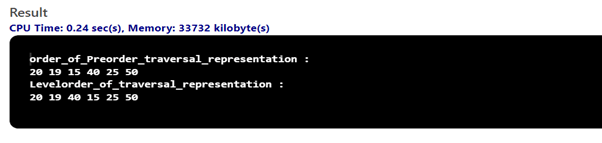
AVLツリーJava

説明: このプログラムは、AVL ツリーポストへの要素の挿入を実行します。これには、取得されたリストが空かどうか、AVL ツリーがローテーションは、事前順序、事後順序、またはレベル順序形式で実行されます。与えられたすべての要素は自動的に入力を受け取り、適切な順序で配置されます。

結論

Java の AVL ツリーは、操作の面で優位性をもたらし、大きなコードセットによって生じる時間の節約と消費に役立つため、多くの開発者に好まれている適切なデータ構造として使用されます。 AVL ツリーには、高さが適切に維持されている場合、挿入、削除、回転、サブツリー全体からの削除などの主要な操作を処理する機能があります。

以上がAVLツリーJavaの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。