
情報を特定の順序で並べ替えることは、多くの場合、配列のようなフレームワーク内で、情報を配置することです。さまざまなシーケンス要件を使用できます。一般的なものは、数値を最小値から最大値へ、またはその逆に並べ替えたり、文字列を辞書順に並べ替えたりすることです。並べ替えの仕組みに興味がある場合は、非効率的だが直感的な代替案から、Java やその他の言語で効果的に実装された効率的なアルゴリズムまで、さまざまなアルゴリズムを取り上げます。
さまざまな並べ替えアルゴリズムがあり、すべてが同じように効果的であるわけではありません。それらを比較し、どれが最もパフォーマンスが高いかを確認するために、時間計算量を分析します。
広告 このカテゴリーの人気コース JAVA マスタリー - スペシャライゼーション | 78 コース シリーズ | 15 回の模擬テスト挿入ソートの背後にある概念は、範囲をソートされたサブ配列とソートされていないサブ配列に分割します。分類された部分は期間 1 の先頭にあり、配列内の最初 (左側) のコンポーネントと一致します。配列内を移動し、反復ごとに配列の分類された部分を 1 コンポーネントずつ拡張します。展開すると、ソートされたサブ配列に新しい要素が配置されます。これを行うには、最初のコンポーネントを変更する必要がなくなるまで、すべての要素を右に移動します。たとえば、次の配列で太字の部分を昇順にソートすると、次のようになります。
コード:
public class InsertionSortEx {
public static void insertionSort(int[] arr) {
for (int x = 1; x < arr.length; x++) {
int current = arr[x];
int y = x - 1;
while(y >= 0 && current < arr[y]) {
arr[y+1] = arr[y];
y--;
}
arr[y+1] = current;
}
}
public static void main(String a[]){
int[] arr1 = {3,5,7,8,4,2,1,9,6};
System.out.println("Before Sorting");
for(int x:arr1){
System.out.print(x+" ");
}
System.out.println();
insertionSort(arr1);//sorting array using insertion sort
System.out.println("After Insertion Sorting");
for(int x:arr1){
System.out.print(x+" ");
}
}
}出力:
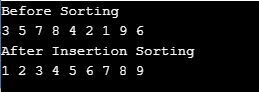
この方法に従って、1 つのコンポーネントがソートされた部分を拡張しました。要素は 4 つではなく 5 つになりました。すべての反復でこれが行われ、配列全体が末尾でソートされます。
注: これは、反復ごとに分類リスト全体を 1 つずつ転送する必要があるためです (O(n))。これを各テーブルの各コンポーネントに対して行う必要があります。これは、テーブルが O(n^2) で区切られていることを意味します。バブルが必要な順序にない場合は、隣接するコンポーネントを置き換えることによって動作します。これは、すべてのコンポーネントが配列の先頭から順番に揃うまで繰り返されます。スワップなしで反復全体を実行できた場合、隣接する要素と比較したすべての項目が望ましい順序になっており、ひいては配列全体も望ましい順序になっていることがわかります。バブルソートアルゴリズムの理由は、数字のようなものが「地面」に「泡立つ」ためです。特定の量に達した後、インスタンスを再度実行すると (4 が適切な例です)、数値がゆっくりと右に移動していることがわかります。
バブルソートの手順は次のとおりです:
コード:
public class BubbleSortExample {
public static void bubbleSort(int[] arr) {
int n = arr.length;
int tmp = 0;
for(int x=0; x < n; x++){
for(int y=1; y < (n-x); y++){
if(arr[y-1] > arr[y]){
//swap elements
tmp = arr[y-1];
arr[y-1] = arr[y];
arr[y] = tmp;
}
}
}
}
public static void main(String[] args) {
int arr[] ={4,2,1,5,3};
System.out.println("Array Before Bubble Sort");
for(int x=0; x < arr.length; x++){
System.out.print(arr[x] + " ");
}
System.out.println();
bubbleSort(arr);
System.out.println("Array After Bubble Sort");
for(int x=0; x < arr.length; x++){
System.out.print(arr[x] + " ");
}
}
}出力:
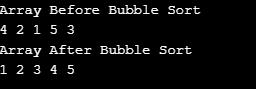
選択ソートは、配列をソートされていない分類の配列に分割します。ただし、今回は、ソート部分配列は、ソートされていない部分配列の最小要素をソートされた配列の末尾に交換によって挿入することによって形成されます。
コード:
public class SelectionSortEx {
public static void selectionSort(int[] arr){
for (int x = 0; x < arr.length - 1; x++)
{
int indx = x;
for (int y = x + 1; y < arr.length; y++){
if (arr[y] < arr[indx]){
indx = y;
}
}
int smallNumber = arr[indx];
arr[indx] = arr[x];
arr[x] = smallNumber;
}
}
public static void main(String a[]){
int[] arr1 = {3,5,1,2,4};
System.out.println("Before Sorting");
for(int x:arr1){
System.out.print(x+" ");
}
System.out.println();
selectionSort(arr1);
System.out.println("After Selection Sorting");
for(int x:arr1){
System.out.print(x+" ");
}
}
}出力:
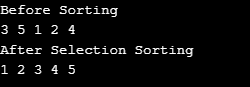
Merge Sort utilizes recursion to fix the issue of the divide and conquest method more effectively than earlier described algorithms.
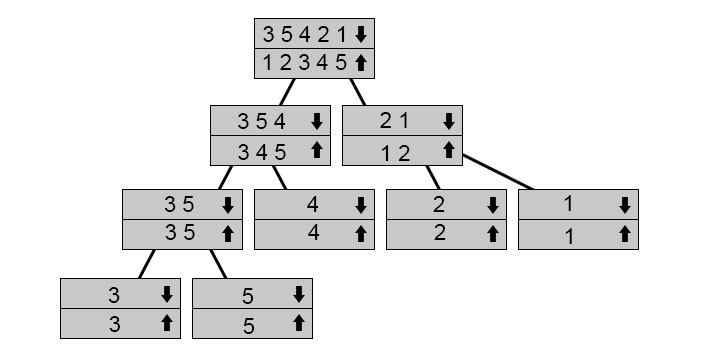
This tree shows how the recursive calls function. Down arrow marked arrays are the arrays for which we call function while we fuse up arrow arrays. Then you follow the arrow to the tree’s edge and then return and merge. We’ve got 3 5 3 1 range, so we split it into 3 5 4 and 2 1. We split them into their parts in order to sort them. We begin fusioning and sorting them as we go when we get to the bottom.
Code:
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
public class MergeSort {
static void merge(int[] array,int lowval,int midval,int highval){
int x, y ,k;
int[] c= new int[highval-lowval+1];
k = 0;
x=lowval;
y=midval+1;
while(x<=midval && y<=highval){
if(array[x]<=array[y]){
c[k++] = array[x++];
}
else{
c[k++] = array[y++];
}
}
while(x<=midval){
c[k++] = array[x++];
}
while(y<=highval){
c[k++] = array[y++];
}
k=0;
for(x = lowval; x<=highval; x++){
array[x] = c[k++];
}
}
static void mergeSort(int[] array,int lowval, int highval){
if(highval-lowval+1>1){
int midval = (lowval+highval)/2;
mergeSort(array,lowval,midval);
mergeSort(array,midval+1,highval);
merge(array,lowval,midval,highval);
}
}
public static void main(String[] args) {
BufferedReader r = new BufferedReader(new InputStreamReader(System.in));
int size;
System.out.println("Enter the array");
try {
size = Integer.parseInt(r.readLine());
} catch (Exception e) {
System.out.println("Please Enter valid Input");
return;
}
int[] array = new int[size];
System.out.println("Enter array elements");
int x;
for (x = 0; x < array.length; x++) {
try {
array[x] = Integer.parseInt(r.readLine());
} catch (Exception e) {
System.out.println("An error Occurred");
}
}
System.out.println("After Sorting");
System.out.println(Arrays.toString(array));
mergeSort(array,0,array.length-1);
System.out.println("Before Merge Sorting");
System.out.println(Arrays.toString(array));
}
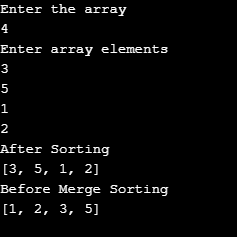
}In this program, we have asked the user to enter input. The output will be in sorted order based on the user’s input.
Output:
You first must know the framework on which Heapsort operates-the heap-in order to comprehend why it operates. We will specifically speak about a binary heap, but you can also generalize this to other heap constructions. A heap is a tree that fulfills the property of the heap, namely that all its kids have relationships to each node. A heap must also be nearly finished. A near-complete d-depth binary has a d-1 subtree with the same root, and each node has a full, left subtree, with a left descending.
In other words, you get a lower and lower number (min-heap) or larger and bigger (max-heap) when moving down the tree. Here is a max-heap instance:
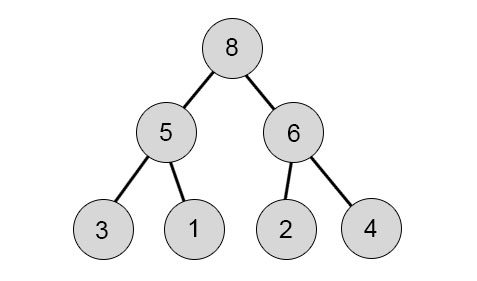
After Repeating this process again, we will get the following results:
Code:
public class HeapSort
{
public void sort(int arr[])
{
int n = arr.length;
for (int x = n / 2 - 1; x >= 0; x--)
heapify(arr, n, x);
for (int x=n-1; x>=0; x--)
int tmp = arr[0];
arr[0] = arr[x];
arr[x] = tmp;
heapify(arr, x, 0);
}
}
void heapify(int arr[], int n, int x)
{
int largest = x;
int L = 2*x + 1;
int r = 2*x + 2;
if (L < n && arr[L] > arr[largest])
largest = L;
if (r < n && arr[r] > arr[largest])
largest = r;
if (largest != x)
{
int swap = arr[x];
arr[x] = arr[largest];
arr[largest] = swap;
heapify(arr, n, largest);
}
}
static void printArray(int arr[])
{
int n = arr.length;
for (int x=0; x<n; ++x)
System.out.print(arr[x]+" ");
System.out.println();
}
public static void main(String args[])
{
int arr[] = {6,1,8,3,5,2,4};
int n = arr.length;
System.out.println("Before Sorting:");
printArray(arr);
HeapSort ob = new HeapSort();
ob.sort(arr);
System.out.println("After Heap Sorting:");
printArray(arr);
}
}Output:
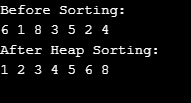
You can view it from point to level of the graph, from left to right. We achieved here that when we have the kth component in the array, the position of its children is 2\*k+1 and 2\*k+2 (assuming that indexing begins at 0). You can monitor this. The position of the parent is always (k-1)/2 for the kth component. You can readily “max heap up” any range because you know that. Check whether one of its kids is lower than that for each component. If so, pair one parent and repeat this step recursively with the parent.
Note: Since iterating for-loops across the entire array makes heapSort) (obviously O(N), it would create Heapsort O’s overall complexity(nlog n). Heapsort has an on-the-spot type, which means that it requires O(1) more room than Merge Sort, but it has some disadvantages, such as parallels that are hard.Sorting is a very prevalent procedure with datasets, whether for further analysis, speeding search with more effective algorithms relying on sorted information, filtering information, etc. Several languages endorse sorting, and often the interfaces obscure what the programmer does.
以上がJava のソートアルゴリズムの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。