最大確率のパス

1514。確率が最大のパス

難易度:中

トピック:配列、グラフ、ヒープ (優先キュー)、最短パス

n 個のノード (0 からインデックス付き) の無向重み付きグラフが与えられます。これは、エッジ リストで表されます。ここで、edges[i] = [a, b] は、横断の成功確率を持つノード a と b を接続する無向エッジです。そのエッジは成功しました。Prob[i].

2 つのノードの開始と終了が与えられた場合、開始から終了までの成功確率が最大となるパスを見つけ、その成功確率を返します。

始点から終点までのパスがない場合は、

0を返します。あなたの答えは、正解と最大1e-5の差がある場合に受け入れられます。

例1:

入力:
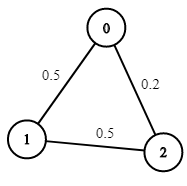
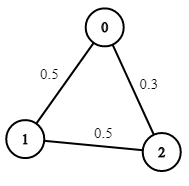
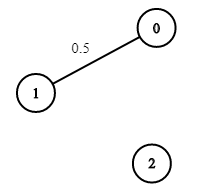
• n = 3、エッジ = [[0,1],[1,2],[0,2]]、succProb = [0.5,0.5,0.2]、開始 = 0、終了 = 2
出力:
• 0.25000
説明:
• 開始から終了まで 2 つのパスがあり、1 つは成功確率 = 0.2、もう 1 つは 0.5 * 0.5 = 0.25 です。

例 2:

入力:
• n = 3、エッジ = [[0,1],[1,2],[0,2]]、succProb = [0.5,0.5,0.3]、開始 = 0、終了 = 2
出力:
• 0.30000

例 3:

入力:
• n = 3、エッジ = [[0,1]]、succProb = [0.5]、開始 = 0、終了 = 2
出力:
• 0.00000
説明:
• 0 と 2 の間にパスはありません。

制約:

2

0

開始 != 終了

0

a != b

0

0

各 2 つのノード間には最大 1 つのエッジがあります

ヒント:

確率を乗算すると精度誤差が生じます。

1. 対数確率を取得して、数値を乗算するのではなく合計します。
2. ダイクストラのアルゴリズムを使用して、すべてのコストを打ち消した後の 2 つのノード間の最小パスを見つけます。

解決策:

ダイクストラのアルゴリズムの修正バージョンを使用できます。最短の道を見つけるのではなく、成功の確率を最大化することになります。

このソリューションを PHP で実装してみましょう:

1514。確率が最大のパス

リーリー
説明：

1. グラフ表現

   : グラフは、各ノードが隣接ノードを指し、それらを接続するエッジの成功確率とともに隣接リストとして表現されます。

2. Max Probability Array

   : 配列 maxProb は、開始ノードから各ノードに到達する最大確率を格納するために使用されます。

3. Priority Queue

   : 最大ヒープ (SplPriorityQueue) は、最も確率の高いパスを最初に探索するために使用されます。これは、宛先ノードに到達したときに、最大の確率でパスが見つかったことを確認するために非常に重要です。

4. アルゴリズム

   :

   開始ノードの確率を 1 として初期化します (開始点に留まる確率が 1 であるため)。
   優先キューを使用してノードを探索し、各近隣ノードに到達する最大確率を更新します。
   目的のノードに到達した場合は、確率を返します。
   パスが存在しない場合は、0を返します。
   出力：

提供された例の場合:

リーリー

出力は0.25になります。

このアプローチでは、確率計算の詳細を処理しながら、ダイクストラのアルゴリズムを使用した効率的なソリューションが保証されます。

連絡先リンク

このシリーズが役立つと思われた場合は、GitHub でリポジトリ

にスターを付けるか、お気に入りのソーシャル ネットワークで投稿を共有することを検討してください。あなたのサポートは私にとってとても意味のあるものになります！

このような役立つコンテンツがさらに必要な場合は、お気軽にフォローしてください:

リンクトイン

• GitHub

以上が最大確率のパスの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。