AI が量子物理学問題を初めて解決、DeepMind が量子励起状態を正確に計算、科学誌に掲載

Editor | KX

以前、Google DeepMind の研究者によって開発されたフェルミオン ニューラル ネットワーク (FermiNet) は、多数の電子の量子基底状態をモデル化するのに非常に適しています。

FermiNet は当初、分子の基底状態に焦点を当てていました。しかし、光や高温にさらされるなどして分子や材料が大量のエネルギーで刺激されると、電子がより高いエネルギー状態、つまり励起状態に入る可能性があります。

励起状態は物理学や化学などの分野で重要ですが、第一原理に基づく励起状態特性のスケーラブルで正確かつ堅牢な計算には依然として重要な理論的課題が残されています。

今回、DeepMind の研究者は、以前の方法よりも強力で汎用性の高い、励起状態を計算するための新しい方法を開発しました。この方法は、FermiNet やその他のニューラル ネットワークを含む、あらゆる種類の数学モデルに適用できます。

提案された方法は、多くの原子や分子の正確な励起状態計算を実現し、深層学習を使用して励起状態特性を計算する既存の方法（特に大規模なシステム）よりもはるかに優れており、さまざまな量子システムに適用できます。

この論文の筆頭著者であり責任著者である David Pfau 氏は、「深層学習が量子物理学における最も困難な問題のいくつかを正確に解決したのはこれが初めてです。私たちは普遍的な量子シミュレーションに向けて新たな一歩を踏み出したいと考えています」と興奮気味に発表しました。

「ニューラルネットワークによる量子励起状態の正確な計算」というタイトルの関連研究がScienceに掲載されました!

論文リンク:https://www.science.org/doi/abs/10.1126/science.adn0137

分子励起状態

分子や材料が大量のエネルギーによって刺激されると、例: 光や高温にさらされると、電子は励起状態と呼ばれる一時的な新しい構造に変化します。

分子が状態間を遷移する際に吸収および放出されるエネルギーの正確な量によって、さまざまな分子や材料に固有のフィンガープリントが作成されます。これは、ソーラーパネルやLEDから半導体や光触媒に至るまでのテクノロジーのパフォーマンスに影響を与えます。また、光合成や視覚など、光が関与する生物学的プロセスでも重要な役割を果たします。

ただし、励起された電子は本質的に量子であるため、このタイプのフィンガープリントをモデル化するのは非常に困難です。つまり、分子内での電子の位置は決して確実ではなく、確率によってのみ表すことができます。

FermiNet は、さまざまな定性的な陽電子結合特性を持つ、さまざまな原子や小分子の基底状態エネルギーを高精度で、場合によっては最先端の状態で生成できます。

しかし、FermiNet は当初、分子の基底状態に焦点を当てていました。しかし、光や高温にさらされるなどして分子や材料が大量のエネルギーで刺激されると、電子がより高いエネルギー状態、つまり励起状態に入る可能性があります。

励起状態のエネルギーを正確に計算することは、基底状態のエネルギーを計算するよりもはるかに困難です。結合クラスターなどの基底状態化学の代表的な方法でさえ、励起状態では数十倍の誤差を示します。研究者らは、FermiNet の研究を励起状態まで拡張したいと考えていましたが、既存の手法では、ニューラル ネットワークを最先端の手法と同等にするには十分なパフォーマンスが得られませんでした。

より強力で汎用性の高い励起状態計算の新しい方法

DeepMind は、変分モンテカルロによって量子系の励起状態を推定するアルゴリズムを提案しています。このアルゴリズムには自由パラメーターがなく、状態の直交化も必要ありません。この問題を、拡張システムの基底状態を見つける問題に変換します。遷移双極子モーメントなどの非対角期待値を含む、任意の観測値を計算できます。

このメソッドは、FermiNet および Psiformer ansatz と組み合わせることで、一連の分子の励起エネルギーと振動子強度を正確に回復することができ、ニューラル ネットワーク解析に特に適しています。

イラスト: リチウムからネオンまでの原子の最初の列の励起状態エネルギー。 NES-VMC を FermiNet に適用した結果。 (出典: 論文)

研究者らは、ニューラル ネットワークの柔軟性と数学的洞察を組み合わせて、システムの励起状態を見つける問題を拡張システムの基底状態を見つける問題に変換できるようにしました。標準の VMC を使用して解決できます。この方法は自然励起状態 VMC (NES-VMC) と呼ばれます。

励起状態の線形独立性は、ansatz の関数形式を介して自動的に課されます。各励起状態のエネルギーおよびその他の観測量は、一重項解析上のハミルトニアン期待値行列を対角化することによって取得され、これらの観測量は追加コストなしで蓄積できます。

결정적으로 이 방법에는 조정할 수 있는 자유 매개변수가 없으며 직교화를 강제하는 페널티 항도 없습니다. 연구원들은 FermiNet과 Psiformer라는 두 가지 신경망 아키텍처를 사용하여 이 접근 방식의 정확성을 조사했습니다.

단일 원자에서 벤젠까지

연구원들은 단일 원자에서 벤젠 크기의 분자까지 진행하는 벤치마크 시스템에서 자신의 방법을 테스트했습니다. 첫 번째 행 원자에 대한 NES-VMC의 정확도는 실험 결과에 매우 가까운 것으로 확인되었으며, 일련의 작은 분자에서는 기존의 최고의 이론적 장치 강도와 비교할 수 있는 고정밀 에너지 및 진동이 얻어졌습니다.

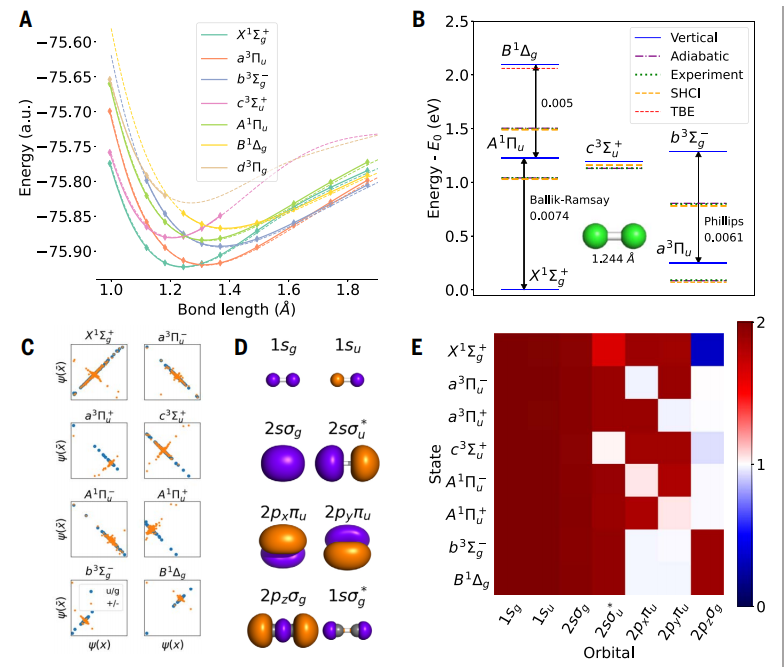
그림: 탄소 이량체의 들뜬 상태. (출처: 논문)

탄소 이량체라고 불리는 작고 복잡한 분자에서 4meV의 평균 절대 오차(MAE)를 달성했는데, 이는 이전 금본위제 계산보다 5배 더 정확합니다.

그림: 들뜬 상태와 에틸렌의 원뿔형 교차점. (출처: 논문)

에틸렌의 경우 NES-VMC는 꼬인 분자의 원추형 교차점을 정확하게 설명하며 고정밀 다중 참조 구성 상호 작용(MR-CI) 결과와 높은 일치를 나타냅니다.

그림: 더 큰 이중 여기 시스템의 들뜬 상태. (출처: 논문)

이 연구에서는 다중 벤젠급 분자를 포함하여 저지대 이중 여기가 있는 5가지 까다로운 시스템도 고려했습니다. 모든 방법이 수직 여기 에너지에 대해 잘 일치하는 시스템에서 Psiformer는 부타디엔을 포함하여 여러 주에서 화학적으로 정확하며, 그 중 일부의 순서는 수십 년 동안 논란이 되어 왔습니다.

몇 년 전의 최첨단 계산이 부정확한 것으로 알려진 테트라진 및 사이클로펜타디에논의 경우 NES-VMC 결과는 최근의 정교한 확산 몬테 카를로(DMC) 및 완전 활성 공간 3차 섭동과 일치하지 않습니다. 이론(CASPT3) 계산은 매우 유사합니다.

그림: 벤젠의 들뜬 상태. (출처: 논문)

마지막으로 벤젠 분자도 연구했는데, 여기서 Psiformer ansatz와 결합된 NES-VMC는 페널티 방법을 사용하는 신경망 ansatz를 포함한 다른 방법에 비해 이론적으로 가장 좋은 추정치로 더 나은 결과를 제공했습니다. 이는 제안된 방법의 수학적 정확성을 검증할 뿐만 아니라 신경망이 현재 계산 방법의 한계에서 분자의 여기 상태를 정확하게 나타낼 수 있음을 보여줍니다.

향후 다체 양자역학에 적용하는 방법

NES-VMC는 매개변수가 없고 수학적으로 타당한 들뜬 상태 변화 원리입니다. 이를 신경망 ansätze와 결합하면 광범위한 벤치마크 문제에서 상당한 정확도를 얻을 수 있습니다.

양자 시스템의 들뜬 상태에 대한 정확한 VMC 방법은 많은 가능성을 열어주고 신경망 파동 함수의 적용 범위를 크게 확장합니다.

이 연구에서는 분자 시스템과 신경망 ansatz의 전자 여기만 고려했지만 NES-VMC는 모든 양자 해밀턴 및 모든 ansatz에 적용 가능하므로 과학자의 진동 전자 결합, 광학에 대한 이해를 향상시킬 수 있는 정확한 계산 연구가 가능합니다. 밴드의 이해 격차, 핵 물리학 및 기타 어려운 문제.

연구원들은 "향후 다체 양자역학의 가장 어려운 문제에 NES-VMC와 심층 신경망이 어떻게 적용될지 기대된다"고 말했다.

참고 내용:

https:/ /x.com/pfau/status/1826681648597135464

https://deepmind.google/discover/blog/ferminet-퀀텀-physics-and-chemistry-from-first-principles/

https:// www.imperial .ac.uk/news/255673/ai-tackles-most-difficult-challenges-퀀텀/

以上がAI が量子物理学問題を初めて解決、DeepMind が量子励起状態を正確に計算、科学誌に掲載の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。