Les détails du travail AIOps de Microsoft révélés

Mesure dynamique, ces données sont principalement divisées en deux catégories : les données de séries chronologiques et les données d'événements. Les données de séries chronologiques font référence à des séries temporelles à valeur réelle (généralement avec des intervalles de temps fixes), telles que l'utilisation du processeur, etc., tandis que les données d'événement font référence à la séquence qui enregistre l'occurrence d'événements spécifiques, tels que les événements de dépassement de mémoire. Afin de garantir la qualité du service produit, de réduire les temps d'arrêt du service et d'éviter des pertes économiques plus importantes, le diagnostic des événements clés du service est particulièrement important. Dans le cadre des travaux d'exploitation et de maintenance réels, lors du diagnostic des événements de service, le personnel d'exploitation et de maintenance peut analyser la cause de l'événement en analysant les données de séries chronologiques liées à l'événement de service. Bien que cette corrélation ne puisse pas refléter avec précision la véritable relation de cause à effet, elle peut néanmoins fournir de bons indices et révélations pour le diagnostic.

La question est alors de savoir comment déterminer automatiquement la relation entre les événements et les données de séries chronologiques ?

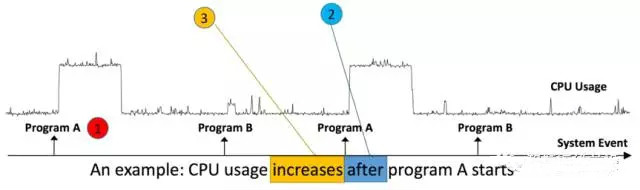
Dans cet article, l'auteur transforme le problème de corrélation de données d'événements (E) et de séries chronologiques (S) en un problème à deux échantillons et utilise la méthode du voisin le plus proche pour déterminer s'il est lié. A principalement répondu à trois questions : A. Existe-t-il une corrélation entre E et S ? B． S’il y a une corrélation, quel est l’ordre chronologique de E et S ? E arrive en premier, ou S arrive en premier ? C. La relation monotone entre E et S. En supposant que S (ou E) apparaît en premier, l’augmentation ou la diminution de S provoque-t-elle l’apparition de E ? Comme le montre la figure, les événements correspondent à l'exécution des programmes A et B, et les données de synchronisation correspondent à l'utilisation du processeur. On peut constater qu'il existe une corrélation entre l'événement (l'exécution du programme A) et les données de synchronisation (utilisation du processeur), et c'est le changement dans l'utilisation du processeur qui augmente après l'exécution du programme A.

L'architecture algorithmique de l'article est principalement divisée en trois parties pour résoudre respectivement les trois problèmes de corrélation, de séquence temporelle et de monotonie. Ces trois parties seront présentées en détail ci-après.

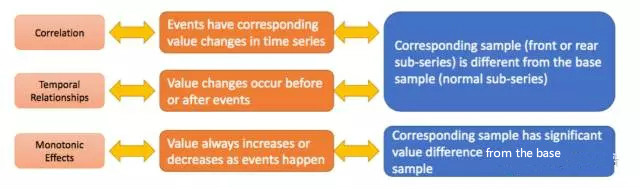
L'article transforme le jugement de corrélation en un problème à deux échantillons. Le cœur du test d'hypothèse à deux échantillons est de déterminer si les deux échantillons proviennent de la même distribution. Tout d’abord, sélectionnez N segments d’échantillons de données de séries chronologiques d’une longueur k correspondant avant (ou après) l’événement, représenté par A1. Le groupe d’échantillons A2 sélectionne au hasard une série d’échantillons de données de longueur k dans la série chronologique. L'ensemble d'échantillons est A1 et va jusqu'à A2. Si E et S sont liés, alors les distributions de A1 et A2 sont différentes, sinon les distributions sont les mêmes. Comment déterminer si les distributions de A1 et A2 sont les mêmes ? Regardons l'exemple suivant :

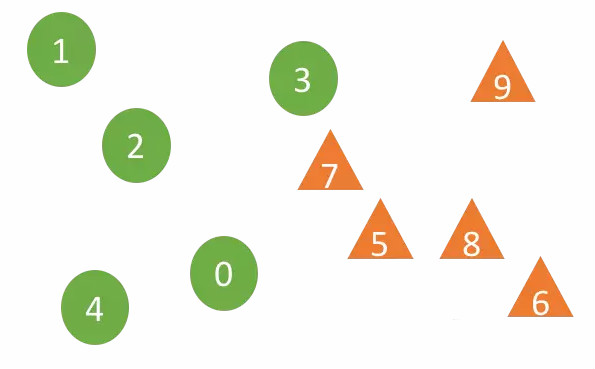
Dans l'image ci-dessus, les échantillons 0 à 4 proviennent du groupe d'échantillons A1 et 5 à 9 appartiennent au groupe d'échantillons A2. L'algorithme DTW est utilisé pour calculer la distance entre les deux échantillons (l'algorithme DTW peut bien s'adapter à l'expansion. et déplacement des données de séquence). Pour un échantillon X appartenant au groupe d'échantillons Ai (i = 1 ou 2), pour les r voisins les plus proches, les échantillons de E et S sont plus liés. Par exemple, si le nombre de voisins est r=2, les deux voisins les plus proches de l’échantillon 7 sont 3 et 5 provenant de deux groupes d’échantillons différents, mais les deux voisins les plus proches de l’échantillon 5 sont 7 et 8 du même groupe d’échantillon A2. L'article utilise le coefficient de confiance (Coefficient de confiance) pour juger de la crédibilité du « test d'hypothèse H1 » (les deux distributions ne sont pas les mêmes, c'est-à-dire que E et S sont liés). H1 crédible est. Il existe deux paramètres clés de l'algorithme : le nombre de voisins les plus proches r et la longueur de la série chronologique k. Le nombre de voisins est le logarithme népérien du nombre d'échantillons. Le premier pic de la courbe de fonction d'autocorrélation des données de la série chronologique est. la longueur de la séquence.

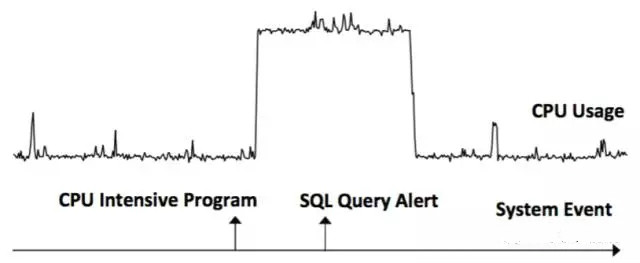
Sélectionnez la séquence avant et après l'événement et la série chronologique sélectionnée au hasard pour calculer la corrélation. Les résultats sont Dr et Df. Si Dr est vrai et Df est faux, cela signifie que E se produit avant que S ne se produise (E -> S). Si Dr est Faux et Df est Vrai, ou Dr est Vrai et Df est Vrai, cela signifie que S se produit avant que E ne se produise (S -> E). Comme le montre l'exemple ci-dessous, l'événement Programme intensif du processeur -> Données de série temporelle Utilisation du processeur, l'événement Utilisation du processeur de données de série temporelle ->

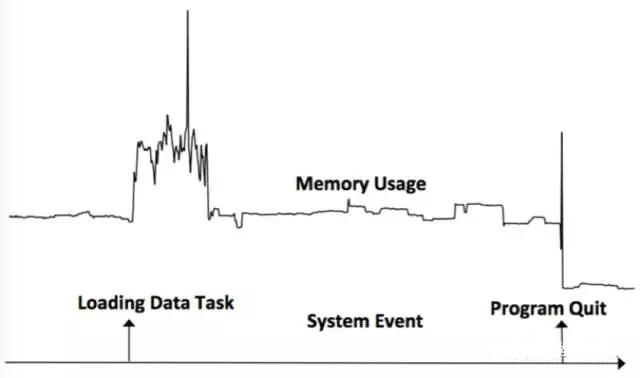
La monotonie est jugée par les changements dans la série temporelle avant et après l'événement. Si la série temporelle après l'événement est supérieure à la valeur de la séquence précédente, la monotonie est augmentée, sinon elle est diminuée. Comme le montre la figure ci-dessous, l'événement de chargement de la tâche de données a provoqué une augmentation de l'utilisation de la mémoire et l'événement Program Quit a provoqué une diminution de l'utilisation de la mémoire.

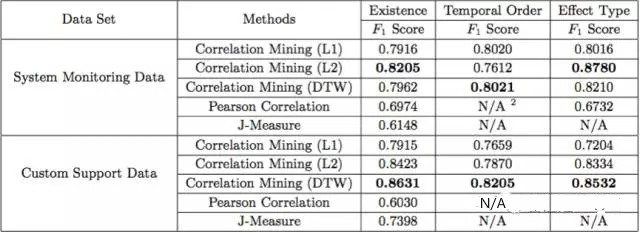
L'article vérifie les performances de l'algorithme en utilisant les données de surveillance du système de Microsoft et les données de l'équipe du service client. Les données sont 24 S (données mémoire, CPU et DISQUE) et 52 E (exécution de tâches spécifiques), 7 S (HTTP. Code d'état) et 57 E (sujet de service), la norme d'évaluation est le score F. Les résultats montrent que la distance DTW fonctionne globalement mieux que les autres distances (L1 et L2) et que l'algorithme fonctionne globalement mieux que les deux algorithmes de base (corrélation de Pearson et mesure J).

L'article présente une nouvelle méthode non supervisée pour étudier la relation entre les événements et les données de séries chronologiques, répondant à trois questions : E et S sont-ils liés ? Dans quel ordre E et S se sont-ils produits ? Et qu’est-ce qu’une relation monotone ? Par rapport à de nombreuses études de corrélation actuelles, qui se concentrent principalement sur la corrélation entre les événements et la corrélation entre les données de séries chronologiques, cet article se concentre sur la relation entre les événements et les données de séries chronologiques. Il est le premier à répondre aux trois questions ci-dessus entre les événements et le temps. données de série.

Le diagnostic des événements a toujours été une tâche très importante dans le domaine de l'exploitation et de la maintenance. La corrélation entre les événements et les données de séries chronologiques peut non seulement fournir une bonne inspiration pour le diagnostic des événements, mais également fournir de bons indices pour l'analyse des causes profondes. L'auteur a vérifié l'algorithme sur l'ensemble de données internes de Microsoft et a obtenu de bons résultats, très précieux pour les milieux académiques et industriels.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!