
Le processus de formation de l'algorithme d'apprentissage par renforcement (Reinforcement Learning, RL) nécessite généralement une grande quantité d'échantillons de données interagissant avec l'environnement à prendre en charge. Cependant, dans le monde réel, il est souvent très coûteux de collecter un grand nombre d'échantillons d'interaction, ou la sécurité du processus d'échantillonnage ne peut être garantie, comme dans le cas de l'entraînement au combat aérien par drone et de l'entraînement à la conduite autonome. Ce problème limite la portée de l’apprentissage par renforcement dans de nombreuses applications pratiques. Par conséquent, les chercheurs ont travaillé dur pour explorer comment trouver un équilibre entre l’efficacité et la sécurité des échantillons afin de résoudre ce problème. Une solution possible consiste à utiliser des simulateurs ou des environnements virtuels pour générer de grandes quantités d’échantillons de données, évitant ainsi les coûts et les risques de sécurité des situations réelles. De plus, afin d'améliorer l'efficacité des échantillons des algorithmes d'apprentissage par renforcement pendant le processus de formation, certains chercheurs ont utilisé la technologie d'apprentissage par représentation pour concevoir des tâches auxiliaires permettant de prédire les signaux d'état futurs. De cette manière, les algorithmes peuvent extraire et coder des caractéristiques pertinentes pour les décisions futures à partir de l’état environnemental d’origine. Le but de cette approche est d’améliorer les performances des algorithmes d’apprentissage par renforcement en apprenant plus d’informations sur l’environnement et en fournissant une meilleure base de prise de décision. De cette manière, l'algorithme peut utiliser les échantillons de données plus efficacement pendant le processus de formation, accélérer le processus d'apprentissage et améliorer la précision et l'efficacité de la prise de décision.
Basé sur cette idée, ce travail a conçu une tâche auxiliaire pour prédire la distribution du domaine fréquentiel de la séquence d'état
pour plusieurs étapes dans le futur afin de capturer les caractéristiques de prise de décision futures à plus long terme et ainsi améliorer l'efficacité de l'échantillon de l'algorithme. .Ce travail s'intitule State Sequences Prediction via Fourier Transform for Representation Learning, publié dans NeurIPS 2023 et accepté comme Spotlight.
Liste des auteurs : Ye Mingxuan, Kuang Yufei, Wang Jie*, Yang Rui, Zhou Wengang, Li Houqiang, Wu Feng
Lien article : https://openreview.net/forum?id= MvoMDD6emT
Lien du code : https://github.com/MIRALab-USTC/RL-SPF/
Contexte et motivation de recherche
Afin d'améliorer l'efficacité des échantillons, les chercheurs ont commencé à se concentrer sur l'apprentissage des représentations, en espérant que les représentations obtenues grâce à la formation pourront extraire des informations riches et utiles sur les caractéristiques de l'état d'origine de l'environnement, améliorant ainsi l'efficacité d'exploration du robot dans le territoire de l'État.
Cadre d'algorithme d'apprentissage par renforcement basé sur l'apprentissage des représentations
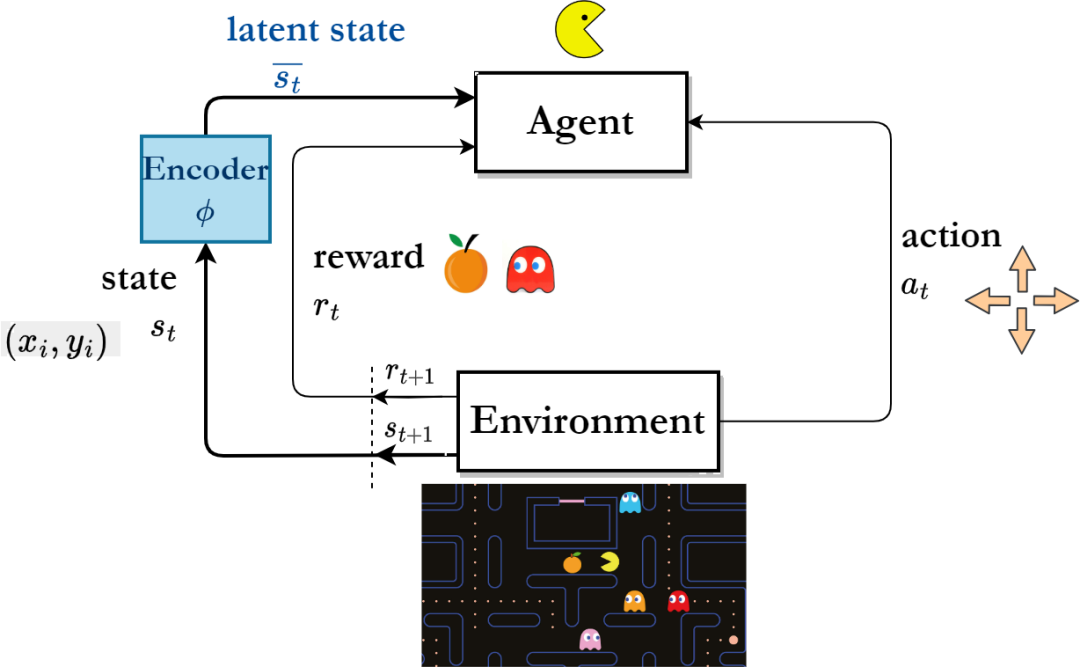
"signaux de séquence à long terme"contiennent plus d'informations futures bénéfiques pour la prise de décision à long terme par rapport aux signaux en une seule étape. Inspirés par ce point de vue, certains chercheurs ont proposé d'aider l'apprentissage des représentations en prédisant les signaux de séquence d'états à plusieurs étapes dans le futur [4,5]. Cependant, il est très difficile de prédire directement la séquence d’états pour faciliter l’apprentissage des représentations.
Parmi les deux méthodes existantes, une méthode génère progressivement l'état futur à un instant donné en apprenant le modèle de transition probabiliste en une seule étape pour prédire indirectement la séquence d'états en plusieurs étapes [6,7]. Cependant, ce type de méthode nécessite une grande précision du modèle de transfert de probabilité formé, car l'erreur de prédiction à chaque étape s'accumulera à mesure que la longueur de la séquence de prédiction augmente.
Un autre type de méthode facilite l'apprentissage des représentations [8] en prédisant directement la séquence d'états de plusieurs étapes dans le futur[8], mais ce type de méthode doit stocker la séquence d'états réels en plusieurs étapes comme étiquette de la tâche de prédiction, qui consomme une grande quantité de stockage. Par conséquent, comment extraire efficacement les informations futures bénéfiques à la prise de décision à long terme à partir de la séquence d’états de l’environnement et ainsi améliorer l’efficacité des échantillons pendant la formation continue du robot de contrôle est un problème qui doit être résolu.
Afin de résoudre les problèmes ci-dessus, nous proposons une méthode d'apprentissage des représentations basée sur la prédiction du domaine fréquentiel des séquences d'états (SSéquences d'état P
rédiction viaFourier Transform, SPF). d'utiliser "Distribution dans le domaine fréquentiel de la séquence d'états" pour extraire explicitement des informations de tendance et de régularité dans les données de séquence d'états, aidant ainsi la représentation à extraire efficacement des informations futures à long terme. Nous avons théoriquement prouvé qu'il existe "deux types d'informations structurelles" dans la séquence d'états, l'une est l'information de tendance liée à la performance de la stratégie, et l'autre est . Informations de régularité liées à la périodicité du statut. Avant d'analyser les deux informations structurelles en détail, nous introduisons d'abord les définitions pertinentes des processus de décision de Markov (MDP) qui génèrent des séquences d'états. Nous considérons le processus de décision markovien classique dans un problème de contrôle continu, qui peut être représenté par un quintuple. Parmi eux se trouvent l'espace d'état et d'action correspondant, la fonction de récompense, la fonction de transition d'état de l'environnement, la distribution initiale de l'état et le facteur d'actualisation. De plus, nous utilisons pour représenter la répartition des actions de la politique dans l'État. Nous enregistrons l'état de l'agent au moment suivant et l'action sélectionnée comme . Une fois que l'agent a entrepris l'action, l'environnement passe à l'état au moment suivant et renvoie des récompenses à l'agent. Nous enregistrons la trajectoire correspondant à l'état et à l'action obtenus lors de l'interaction entre l'agent et l'environnement sous la forme , et la trajectoire obéit à la distribution. L'objectif de l'algorithme d'apprentissage par renforcement est de maximiser le rendement cumulé attendu dans le futur. Nous utilisons pour représenter le rendement cumulé moyen dans le cadre de la stratégie et du modèle d'environnement actuels, et nous l'abrégeons comme suit : montre la performance de la stratégie actuelle. Ci-dessous, nous présentons la "première caractéristique structurelle" de la séquence d'états, qui implique la dépendance entre la séquence d'états et la séquence de récompense correspondante, et peut montrer la performance de la stratégie actuelle. Tendance . Dans les tâches d'apprentissage par renforcement, la séquence d'états futurs détermine en grande partie la séquence d'actions entreprises par l'agent dans le futur, et détermine en outre la séquence de récompense correspondante. Par conséquent, la séquence d’états futurs contient non seulement des informations sur la fonction de transition de probabilité inhérente à l’environnement, mais peut également aider à capturer la tendance de la stratégie actuelle. Inspirés par la structure ci-dessus, nous avons prouvé le théorème suivant pour démontrer davantage l'existence de cette dépendance structurelle : Théorème 1 : Si la fonction de récompense est uniquement liée à l'état, alors pour deux stratégies quelconques et , leur différence de performance peut être contrôlée par la différence dans la distribution des séquences d'états produites par ces deux stratégies : Dans la formule ci-dessus, représente la distribution de probabilité de la séquence d'états dans les conditions de la stratégie spécifiée et de la probabilité de transition fonction et représente la norme. Le théorème ci-dessus montre que plus la différence de performances entre les deux stratégies est grande, plus la différence de distribution entre les deux séquences d'états correspondantes est grande. Cela signifie qu'une bonne stratégie et une mauvaise stratégie produiront deux séquences d'états très différentes, ce qui illustre en outre que les informations structurelles à long terme contenues dans la séquence d'états peuvent potentiellement affecter l'efficacité de la stratégie de recherche avec d'excellentes performances. D'un autre côté, sous certaines conditions, la différence de distribution dans le domaine fréquentiel de la séquence d'états peut également fournir une limite supérieure pour la différence de performance politique correspondante, comme le montre le théorème suivant : Théorème 2 : Si l'état L'espace est de dimension finie et que la fonction de récompense est un polynôme à n degrés lié à l'état, alors pour deux stratégies et , leur différence de performance peut être contrôlée par la différence de distribution dans le domaine fréquentiel des séquences d'état générées. par ces deux stratégies : Dans la formule ci-dessus, représente la fonction de Fourier de la séquence de puissance de la séquence d'états générée par la politique, et représente la ième composante de la fonction de Fourier. Ce théorème montre que la distribution du domaine fréquentiel de la séquence d'états contient toujours des caractéristiques qui sont pertinentes pour la performance politique actuelle. Nous introduisons maintenant la "deuxième caractéristique structurelle" qui existe dans la séquence d'états, qui implique la dépendance temporelle entre les signaux d'état, c'est-à-dire la séquence d'états sur une longue période de temps. motif régulier exposé. Dans de nombreuses tâches de scénarios réels, les agents afficheront également un comportement périodique car la fonction de transition d'état de leur environnement est elle-même périodique. Prenons l'exemple d'un robot d'assemblage industriel. Le robot est formé pour assembler des pièces ensemble pour créer un produit final. Lorsque la formation stratégique atteint la stabilité, il exécute une séquence d'actions périodiques qui lui permet d'assembler efficacement les pièces dans Together. Inspirés de l'exemple ci-dessus, nous proposons une analyse théorique pour prouver que dans l'espace d'états fini, lorsque la matrice de probabilité de transition satisfait certaines hypothèses, la séquence d'états correspondante peut s'afficher "progressivement" lorsque l'agent atteint une stratégie stable. . Presque périodicité", le théorème spécifique est le suivant : Théorème 3 : Pour un espace d'état de dimension finie avec une matrice de transition d'état de , en supposant qu'il existe des classes cycliques, la sous-matrice de transition d'état correspondante. est. Supposons que le nombre de valeurs propres de module 1 de cette matrice soit , alors pour la distribution initiale de tout état , la distribution d'état montre une périodicité asymptotique avec une période . Dans la tâche MuJoCo, lorsque la formation politique atteint la stabilité, l'agent montrera également des mouvements périodiques. La figure ci-dessous donne un exemple de la séquence d'états de l'agent HalfCheetah dans la tâche MuJoCo sur une période de temps, et une périodicité évidente peut être observée. (Pour plus d'exemples de séquences d'états périodiques dans la tâche MuJoCo, veuillez vous référer à la section E en annexe de cet article) La périodicité de l'état de l'agent HalfCheetah dans la tâche MuJoCo sur une période de temps Les informations présentées par séries chronologiques dans le domaine temporel sont relativement dispersées, mais dans le domaine fréquentiel, les informations régulières dans la séquence sont présentées sous une forme plus concentrée. En analysant les composantes fréquentielles dans le domaine fréquentiel, nous pouvons capturer explicitement les caractéristiques périodiques présentes dans la séquence d'états. Dans la partie précédente, nous avons théoriquement prouvé que la distribution dans le domaine fréquentiel de la séquence d'états peut refléter les performances de la stratégie, et en analysant les composantes fréquentielles dans le domaine fréquentiel, nous pouvons explicitement capturer les caractéristiques périodiques de la séquence d’états. Inspirés par l'analyse ci-dessus, nous avons conçu la tâche auxiliaire de "Prédire la transformée de Fourier d'une séquence d'états futurs à étapes infinies" pour encourager la représentation afin d'extraire des informations structurelles dans la séquence d'états. Ce qui suit présente notre modélisation de cette tâche auxiliaire. Compte tenu de l'état et de l'action actuels, nous définissons l'attente de la séquence d'états futurs comme suit : Notre tâche auxiliaire entraîne une représentation pour prédire la transformée de Fourier en temps discret (DTFT) de l'attente de la séquence d'états ci-dessus), qui est, La formule de transformée de Fourier ci-dessus peut être réécrite sous la forme récursive suivante : où où, Les dimensions de l'espace d'état sont le nombre de points de discrétisation de la fonction de Fourier de la séquence d'états prédite. Inspirés par la fonction de perte d'erreur TD [9] qui optimise les réseaux de valeurs Q dans Q-learning, nous avons conçu la fonction de perte suivante : Parmi eux, se trouvent respectivement les paramètres du réseau neuronal de l'encodeur de représentation (encodeur) et du prédicteur de la fonction de Fourier (prédicteur) pour lesquels la fonction de perte doit être optimisée, et constituent le pool d'expérience pour stocker des exemples de données. De plus, nous pouvons prouver que la formule récursive ci-dessus peut être exprimée sous forme d'application de compression : Théorème 4 : Représentons la famille de fonctions , et définissons la norme sur où représente le vecteur ligne de la matrice . Nous définissons la cartographie comme et il peut être prouvé qu'il s'agit d'une cartographie compressée. Selon le principe du mappage de compression, nous pouvons utiliser l'opérateur de manière itérative pour approximer la distribution du domaine fréquentiel de la séquence d'état réel et avoir une garantie de convergence dans un cadre tabulaire. De plus, la fonction de perte que nous avons conçue dépend uniquement de l'état du moment actuel et du moment suivant, il n'est donc pas nécessaire de stocker les données d'état de plusieurs étapes futures comme étiquettes de prédiction, ce qui présente les avantages de "mise en œuvre simple et faible volume de stockage" . Nous introduisons maintenant le cadre d'algorithme de la méthode (SPF) dans cet article. Nous saisissons les données d'état-action du moment actuel et du moment suivant dans en ligne (en ligne) et cible ( cible) respectivement) Dans l'encodeur de représentation (encodeur), les données de représentation état-action sont obtenues, puis les données de représentation sont entrées dans le prédicteur de fonction de Fourier (prédicteur) pour obtenir deux ensembles de prédictions de fonction de Fourier de séquence d'état au moment actuel et la valeur du moment suivant. En remplaçant ces deux ensembles de prédictions de la fonction de Fourier, nous pouvons calculer la valeur de la fonction de perte. Nous optimisons et mettons à jour l'encodeur de représentation et le prédicteur de fonction de Fourier en minimisant la fonction de perte, afin que la sortie du prédicteur puisse se rapprocher de la transformée de Fourier de la séquence d'état réel, encourageant ainsi l'encodeur de représentation à extraire les caractéristiques qui contiennent le avenir à long terme Caractéristiques de l'information structurelle des séquences d'états. Nous saisissons l'état et l'action d'origine dans l'encodeur de représentation, utilisons les caractéristiques obtenues comme entrée du réseau d'acteurs et du réseau critique dans l'algorithme d'apprentissage par renforcement, et utilisons l'algorithme d'apprentissage par renforcement classique pour optimiser le réseau d'acteurs et le réseau critique réseau. Résultats expérimentaux (Remarque : cette section ne sélectionne qu'une partie des résultats expérimentaux. Pour des résultats plus détaillés, veuillez vous référer à la section 6 et à l'annexe de l'article original.) Nous allons SPF La méthode a été testée sur l'environnement de contrôle du robot de simulation MuJoCo, et les six méthodes suivantes ont été comparées : La figure ci-dessus montre les courbes de performances de notre méthode SPF proposée (ligne rouge et ligne orange) et d'autres méthodes de comparaison dans 6 tâches MuJoCo. Les résultats montrent que notre méthode proposée peut atteindre une amélioration des performances de 19,5% par rapport aux autres méthodes. Nous avons mené des expériences d'ablation sur chaque module de la méthode SPF, en comparant cette méthode avec la non-utilisation du module projecteur (noproj), la non-utilisation du module réseau cible (notarg) et la modification de la perte de prédiction (nofreqloss) , comparez les performances lors de la modification de la structure du réseau de l'encodeur de fonctionnalités (mlp, mlp_cat). Diagramme des résultats de l'expérience d'ablation de la méthode SPF appliquée à l'algorithme SAC, testé sur la tâche HalfCheetah Nous utilisons la méthode SPFprédicteur entraînépour sortir le Fu de la fonction de Fourier de la séquence d'états et la séquence d'états de 200 étapes récupérée via la Transformation de Fourier inverse sont comparées à la séquence d'états réelle de 200 étapes. Les résultats montrent que même si un état plus long est utilisé comme entrée, la séquence d'états récupérée est très similaire à la séquence d'états réels. Cela montre que la représentation apprise par la méthode SPF peut effectivement coder la structure contenue dans l'état. informations sur la séquence. Analyse des informations structurelles dans la séquence d'états
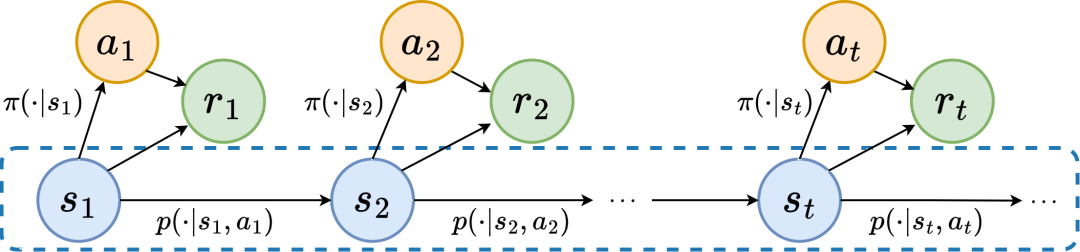
Processus de décision de Markov
Informations sur les tendances
Informations régulières
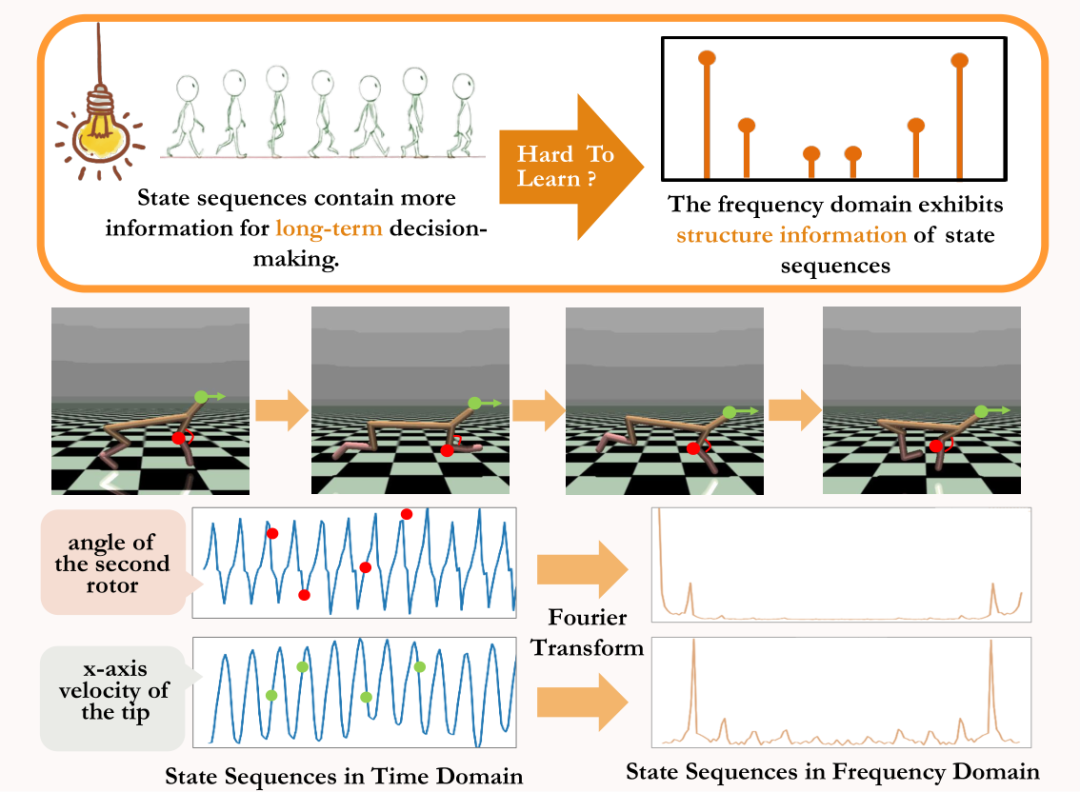
Introduction à la méthode
Fonction de perte de méthode SPF
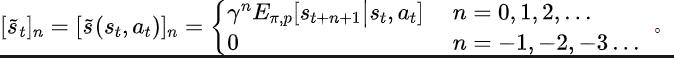
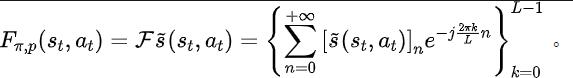
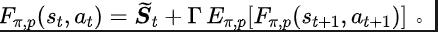
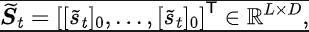

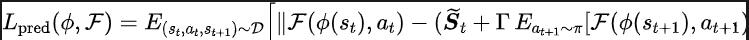
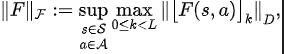
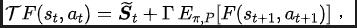
Cadre d'algorithme de la méthode SPF
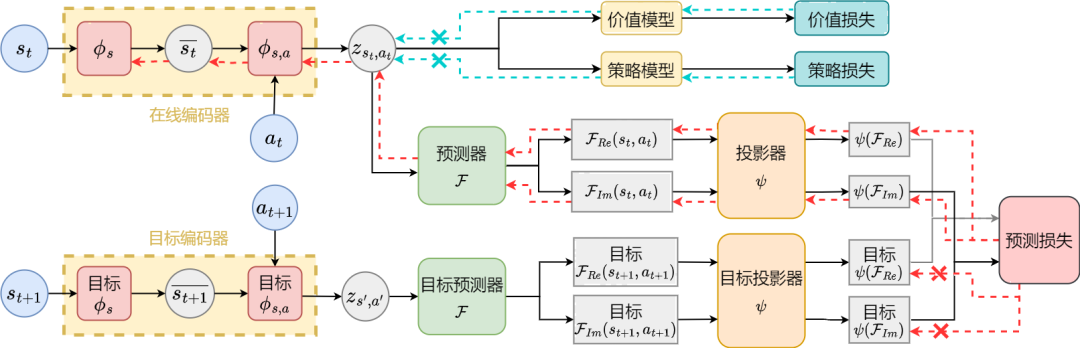 Schéma cadre d'algorithme de la méthode d'apprentissage de représentation (SPF) basé sur la prédiction du domaine fréquentiel de séquence d'état
Schéma cadre d'algorithme de la méthode d'apprentissage de représentation (SPF) basé sur la prédiction du domaine fréquentiel de séquence d'état
Comparaison des performances de l'algorithme
Expérience d'ablation
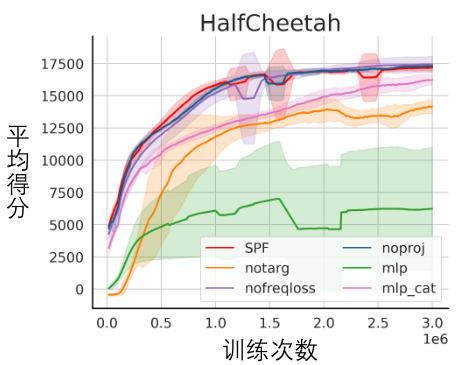
Expérience de visualisation
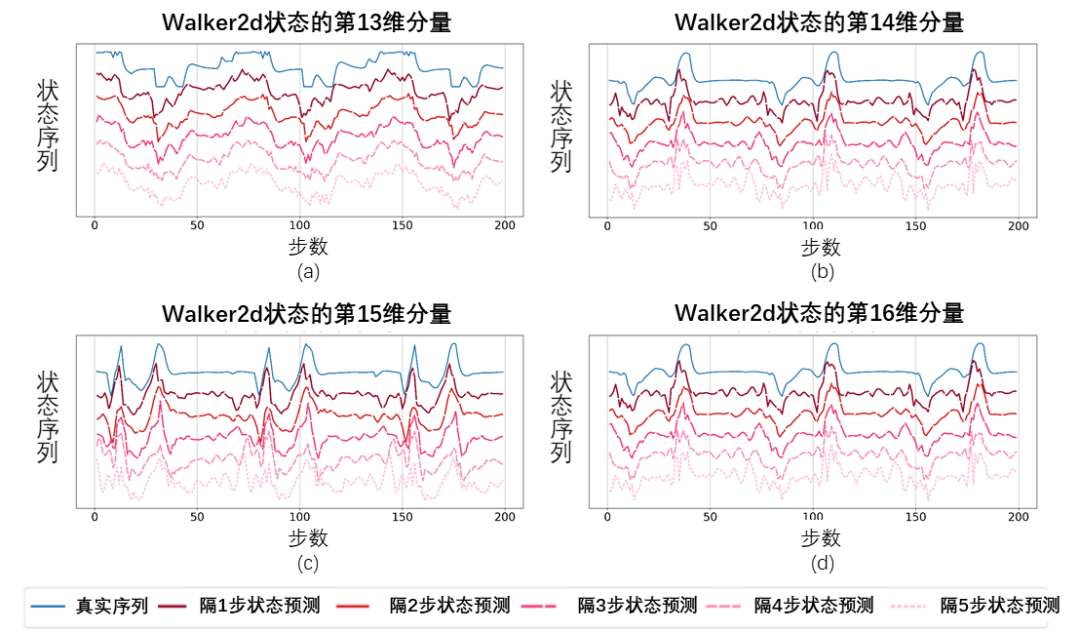 Diagramme schématique de la séquence d'états récupérée sur la base de la valeur prédite de la fonction de Fourier, testée sur la tâche Walker2d. Parmi eux, la ligne bleue est un diagramme schématique de la séquence d'états réels, et les cinq lignes rouges sont un diagramme schématique de la séquence d'états restaurée. Les lignes rouges inférieures et plus claires représentent la séquence d'états restaurée en utilisant l'état historique plus long.
Diagramme schématique de la séquence d'états récupérée sur la base de la valeur prédite de la fonction de Fourier, testée sur la tâche Walker2d. Parmi eux, la ligne bleue est un diagramme schématique de la séquence d'états réels, et les cinq lignes rouges sont un diagramme schématique de la séquence d'états restaurée. Les lignes rouges inférieures et plus claires représentent la séquence d'états restaurée en utilisant l'état historique plus long.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 Comment lier des données dans une liste déroulante
Comment lier des données dans une liste déroulante
 Méthode de réparation des doutes sur la base de données
Méthode de réparation des doutes sur la base de données
 Comment utiliser le paramètre Oracle
Comment utiliser le paramètre Oracle
 Explication détaillée de la configuration de nginx
Explication détaillée de la configuration de nginx
 Comment résoudre l'échec de la résolution DNS
Comment résoudre l'échec de la résolution DNS
 Quelles sont les fonctions des réseaux informatiques
Quelles sont les fonctions des réseaux informatiques
 Comment utiliser le commutateur Java
Comment utiliser le commutateur Java
 Comment ouvrir le panneau de configuration Win11
Comment ouvrir le panneau de configuration Win11