
double f=0,0005;
double i=3;
double d=f*i;
double f1=0.0005;
double j=3;
double d1=f1*j;
si(d==d1){
System.out.println("aaa");
} C'est équivalent. Le type de données de base en Java est appelé une variable automatique. Puisque la taille des données et la durée de vie des valeurs littérales sont connues, elles sont placées sur la pile pour des raisons de vitesse. Les données peuvent être partagées. Par exemple, int a=3 int b=3, le compilateur traite d'abord int a=3, il créera d'abord une référence à la variable a sur la pile, puis recherchera l'adresse avec a ; valeur littérale égale à 3. Sinon, il ouvrira une adresse pour stocker la valeur littérale 3, puis traitera int b=3 après avoir créé l'application avec la variable b, trouvera s'il existe une adresse avec la valeur littérale 3 ; Maintenant que c'est le cas, il pointe vers l'adresse 3. À ce stade, utiliser == (pour juger si les adresses sont les mêmes) sera True
1. Performances en virgule flottante, anciennement appelées coprocesseur, 486 n'était pas inclus dans le CPU auparavant (8086~8087, 80286~80287, 80386~80387=80386DX, 80486SX~80487=80486DX, 586=586+587… ...) L'arithmétique à virgule flottante est une méthode arithmétique de haute précision principalement utilisée en science et en multimédia.
2. Cela peut être compris comme une méthode de fonctionnement dans laquelle la virgule décimale peut être déplacée. Vitesse actuelle AMD>>Inter
3. Les nombres à virgule flottante font référence à des nombres rationnels avec des décimales limitées, telles que -10,8, 0,00, 25,01, etc.
4. Opération à virgule flottante, le résultat est un nombre à virgule flottante et la partie décimale du résultat du calcul sera conservée.
Par exemple : lors de l'utilisation de l'arithmétique à virgule flottante, 100,0÷3,0=33,33333333.
5. Par exemple, si une balle touche le mur et qu'un morceau de terre tombe, de puissants calculs en virgule flottante peuvent afficher la poussière qui tombe.
J'espère adopter
3.14 est simple précision et 3.14159 est double précision.
La différence entre les deux est la suivante :
1. Différentes références
1. Simple précision : fait référence à une manière pour les ordinateurs d'exprimer des approximations de nombres réels.
2. Double précision : ce type de données est similaire au type de données simple précision (float), mais a une précision supérieure à celle du float.
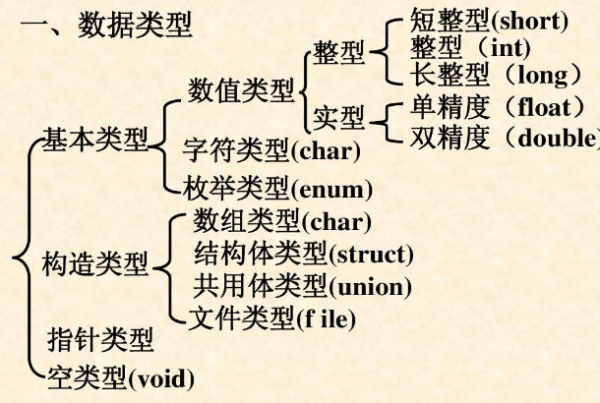
2. Espace occupé différent
1. Simple précision : La plage va de -3.402823E38 à -1.401298E-45 lorsque le nombre est négatif, et de 1.401298E-45 à 3.402823E38 lorsque le nombre est positif.
2. Double précision : le type double précision occupe 8 octets (64 bits) d'espace mémoire et sa plage de valeurs est de -1,79769313486232E308 à 1,79769313486232E308.
3. Différentes caractéristiques
1. Simple précision : lorsque la valeur est inférieure à la valeur ci-dessus, la précision sera progressivement perdue en raison de la réduction du nombre de chiffres significatifs de la mantisse (comme spécifié dans IEEE 754), ou certains systèmes utilisent directement la valeur. 0 pour simplifier le processus de traitement.
2. Double précision : L'espace mémoire occupé lors de la compilation varie selon les différents compilateurs. Il s'agit d'un type de données double float, un type de variable qui représente des variables réelles en C/C++.
Source de référence : Encyclopédie Single Precision
Source de référence : Encyclopédie-Point flottant double précision
La virgule flottante est obtenue en multipliant un nombre entier ou à virgule fixe (c'est-à-dire la mantisse) par une puissance entière d'une certaine base (généralement 2 en ordinateur). Cette méthode de représentation est similaire à la notation scientifique en base 10.
Le nombre à virgule flottante a est représenté par deux nombres m et e : a = m * b^e (b élevé à la puissance e).
Dans un tel système, nous choisissons une base b (la base du système de notation) et une précision p (c'est-à-dire le nombre de bits à utiliser pour le stockage). m (c'est-à-dire la mantisse) est un nombre de p chiffres sous la forme ±d.ddd...ddd (chaque bit est un entier compris entre 0 et b-1, y compris 0 et b-1). Si le premier bit de m est un entier non nul, m est dit normalisé.
Certaines descriptions utilisent un bit de signe distinct (s représente + ou -) pour indiquer positif ou négatif, donc m doit être positif. e est l'exposant.
Nous pouvons utiliser ces 3 méthodes pour représenter les nombres à virgule flottante :
1.Code BCD.
2. La représentation de la mantisse du code exposant.
3. Nous pouvons transformer la deuxième méthode pour obtenir une meilleure méthode. Déplacez d'abord la virgule décimale d'un nombre à virgule flottante jusqu'à la fin et exprimez-la avec N=M*RC, R=10, puis convertissez M en binaire B, puis utilisez C comme code d'exposant et utilisez B comme mantisse pour exprimer en utilisant la méthode de la mantisse du code exposant.
Par exemple : 3,14159=314159*10^(-5).
314159 est représenté en binaire par 1001100101100101111.
L'utilisation de cette méthode peut non seulement représenter avec précision la valeur des nombres à virgule flottante, mais également utiliser pleinement l'espace de stockage.

Informations détaillées :
Unité à virgule flottante (FPU)
Les opérations en virgule flottante sont différentes des opérations sur les nombres entiers, donc les unités arithmétiques sont bien sûr différentes. Les premiers processeurs à virgule flottante sont apparus comme des « coprocesseurs externes » pour le processeur. Le FPU x87 fait spécifiquement référence à l'architecture de coprocesseur à virgule flottante utilisée avec les processeurs x86.
Voici les points suivants :
1. Les registres à virgule flottante adoptent une structure de pile.
La profondeur est de 8 et la largeur est de 80 bits, soit 8 registres de 80 bits.
Les noms sont ST(0) ~ ST(7), le haut de la pile est ST(0) et les nombres sont respectivement 0 ~ 7.
2. Toutes les opérations en virgule flottante sont effectuées avec une précision étendue de 80 bits.
3. Les nombres à virgule flottante sont transférés entre les registres à virgule flottante et la mémoire.
(1) Les variables de type float, double et long double sont représentées en mémoire en utilisant respectivement la simple précision, la double précision et la précision étendue IEEE 754, occupant respectivement 32 bits, 64 bits et 96 bits (les 16 premiers bits ne sont pas valides). .
(2) Les variables de type float, double et long double sont représentées par une précision étendue de 80 bits dans les registres à virgule flottante.
(3) Du registre à virgule flottante à la mémoire : le format de précision étendue 80 bits est converti en 32 bits ou 64 bits.
(4) De la mémoire au registre à virgule flottante : conversion 32 bits ou 64 bits au format de précision étendue 80 bits.
Source de référence : Encyclopédie-Point flottant
Encyclopédie-Représentation à virgule flottante
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 mot en ppt
mot en ppt
 qu'est-ce que json
qu'est-ce que json
 Quel logiciel est Autocad ?
Quel logiciel est Autocad ?
 utilisation de l'état d'affichage
utilisation de l'état d'affichage
 Comment ouvrir la fenêtre du terminal dans vscode
Comment ouvrir la fenêtre du terminal dans vscode
 Comment supprimer des éléments de tableau en JavaScript
Comment supprimer des éléments de tableau en JavaScript
 Pourquoi toutes les icônes dans le coin inférieur droit de Win10 apparaissent-elles ?
Pourquoi toutes les icônes dans le coin inférieur droit de Win10 apparaissent-elles ?
 Que s'est-il passé lorsque la 4G est devenue 2G ?
Que s'est-il passé lorsque la 4G est devenue 2G ?