Terence Tao utilise l'assistant de vérification de modèles à grande échelle Lean pour montrer sa préférence

"Je prédis que, si elle est utilisée correctement, l'IA deviendra un co-auteur de confiance dans la recherche mathématique et dans de nombreux autres domaines d'ici 2026", a déclaré le mathématicien Terence Tao dans un blog précédent.

Tao Zhexuan a dit cela et l'a fait.

Il a récemment mené des recherches mathématiques à l'aide d'outils tels que GPT-4, Copilot et Lean, et a également découvert un bug caché dans son article avec l'aide de l'IA.

Récemment, Terence Tao a déclaré que le projet Lean4 avait achevé avec succès la formalisation de la preuve de la conjecture polynomiale de Freiman-Ruzsa (PFR), qui n'a pris que trois semaines. Dans le même temps, le compilateur Lean rapporte également que la conjecture est conforme aux axiomes standards. Il s'agit d'un grand succès de la preuve assistée par ordinateur et par l'IA, et c'est passionnant

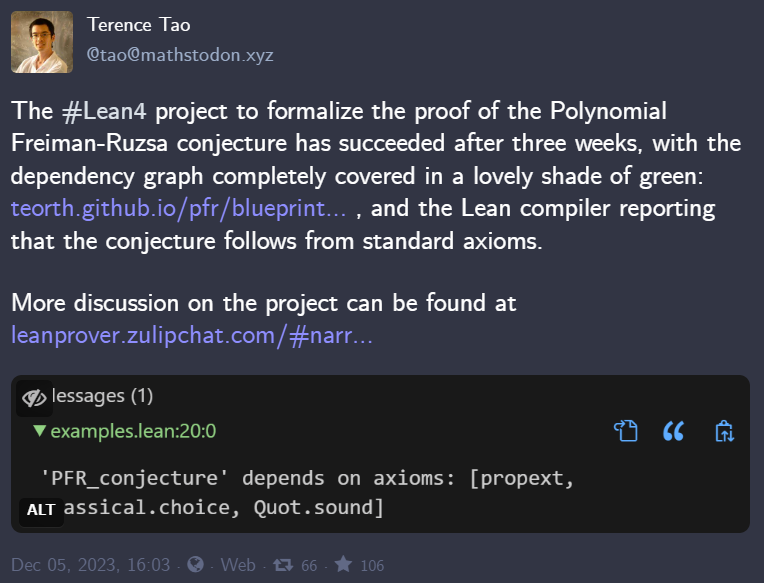
Pour plus d'informations sur la recherche ci-dessus, les lecteurs intéressés peuvent se référer à « Quelle est la preuve formelle de Tao Zhexuan utilisant l'IA ? Comprenez la vie passée et présente de la conjecture PFR dans un seul article.

En voyant cela, des lecteurs attentifs ont peut-être découvert l'indice que Maître Tao a mentionné à plusieurs reprises lors de recherches mathématiques. En termes simples, Lean est un langage de programmation qui aide les mathématiciens à vérifier des théorèmes, où les utilisateurs peuvent rédiger et vérifier des preuves. Par rapport au Lean original, la dernière version Lean 4 présente de nombreuses optimisations, notamment un compilateur plus rapide, une gestion améliorée des erreurs et une meilleure intégration avec des outils externes.

Lean est largement utilisé dans le domaine des mathématiques Aujourd'hui, alors que les grands modèles (LLM) sont populaires, existe-t-il une meilleure façon de combiner les deux ?

Quelqu'un l'a déjà implémenté. L'équipe de la plateforme ouverte LeanDojo (pour LeanDojo, veuillez vous référer à "Le grand modèle d'IA aide Tao Zhexuan à résoudre des problèmes, peut-il également prouver des théorèmes mathématiques ? ") et la recherche. du California Institute of Technology L'auteur a lancé Lean Copilot, un outil de collaboration conçu pour le LLM et l'interaction humaine, visant à donner des preuves mathématiques formelles 100 % précises grâce à la collaboration homme-machine.

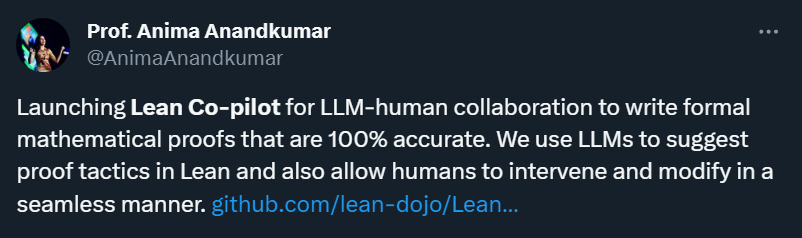
Il convient de noter que les recherches de l'équipe LeanDojo se concentrent principalement sur l'utilisation du LLM pour automatiser la preuve de théorèmes. À partir de là, il n'est pas difficile de voir que le Lean Copilot qu'ils ont lancé est lié au LLM. être surprenant.

Adresse du projet : https://github.com/lean-dojo/LeanCopilot

Pour cette recherche, en plus de dire cool, cela signifie très cool, et l'évaluation est toujours très élevée.

Utilisez le LLM dans Lean pour accélérer la preuve mathématique

La preuve automatisée des théorèmes a toujours été confrontée à de nombreuses difficultés. Traditionnellement, la preuve mathématique repose sur une dérivation manuelle et nécessite une vérification méticuleuse. Aujourd'hui, avec les progrès de l'IA, les chercheurs ont commencé à utiliser l'intelligence artificielle pour mener une exploration approfondie, mais ce problème est inévitable, c'est-à-dire que le LLM n'est parfois pas très fiable dans les tâches de mathématiques et de raisonnement, et est sujet aux erreurs et aux hallucinations.

La fonction de Lean Copilot est de permettre aux utilisateurs d'utiliser de grands modèles de langage pour automatiser le processus de preuve en Lean et augmenter la vitesse de synthèse des preuves. Les utilisateurs peuvent également intervenir et modifier en toute transparence si nécessaire, obtenant ainsi une collaboration équilibrée entre l'intelligence artificielle et l'intelligence humaine.

Grâce à Lean Copilot, LLM peut être utilisé dans Lean pour réaliser une automatisation des preuves, y compris des suggestions de stratégie, des prémisses et des preuves de recherche

Les utilisateurs peuvent choisir d'utiliser les modèles intégrés fournis par LeanDojo ou d'importer leurs propres modèles. Ces modèles peuvent être exécutés localement (avec ou sans GPU) ou dans le cloud

En bref, Lean Copilot offre aux utilisateurs un moyen flexible d'améliorer et d'optimiser la démonstration de théorèmes dans Lean en introduisant le processus LLM.

Les principales fonctionnalités du Lean Copilot peuvent être résumées ainsi :

• LLM est capable de proposer des étapes de preuve, de rechercher des preuves et de sélectionner des lemmes utiles dans une grande bibliothèque mathématique.
• Lean Copilot peut être configuré en tant que package Lean et fonctionne de manière transparente dans le flux de travail VS Code de Lean.
• Les utilisateurs peuvent utiliser les modèles intégrés dans LeanDojo ou utiliser leurs propres modèles, qui peuvent être exécutés localement (avec ou sans GPU) ou dans le cloud.
• Cet outil fonctionne sur diverses plates-formes, notamment Linux, macOS et Windows WSL.

Pour rendre le LLM plus accessible aux utilisateurs du Lean, Lean Copilot espère démarrer une boucle de rétroaction positive : prouver que l'automatisation conduira à de meilleures données et, à terme, améliorera les performances mathématiques du LLM.

Démonstration de l'effet Copilot

Vous pouvez configurer Lean Copilot selon le tutoriel officiel Une fois la configuration terminée, vous pouvez démarrer l'expérience. L'auteur du projet fournit également quelques exemples officiels à titre de référence

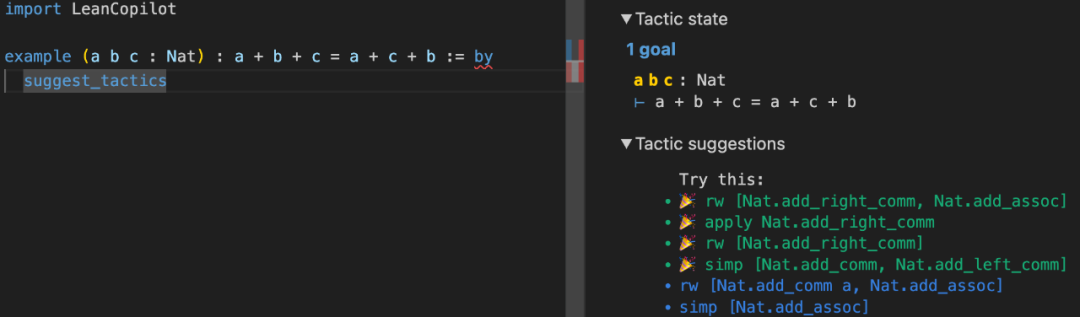
solutions recommandées. Après avoir importé LeanCopilot, vous pouvez utiliser suggest_tactics pour générer des solutions recommandées. Lors de l'utilisation, vous pouvez également cliquer sur la solution recommandée et l'utiliser dans la preuve (voir l'image ci-dessous)

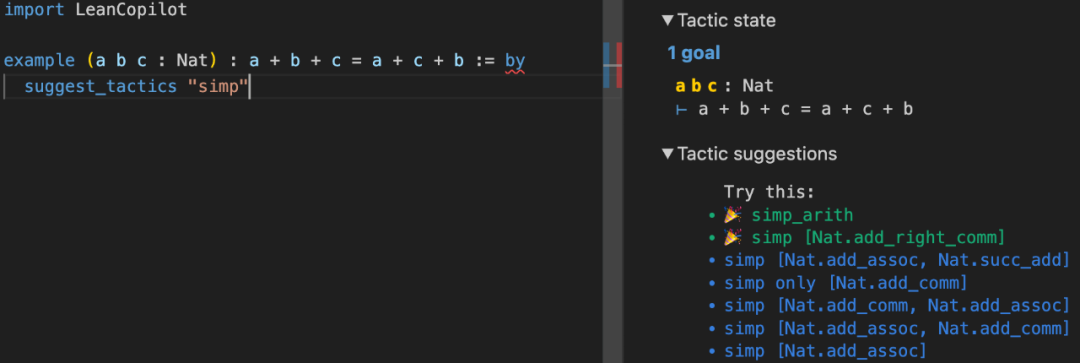
Vous pouvez utiliser un préfixe, tel que simp, pour limiter la stratégie générée

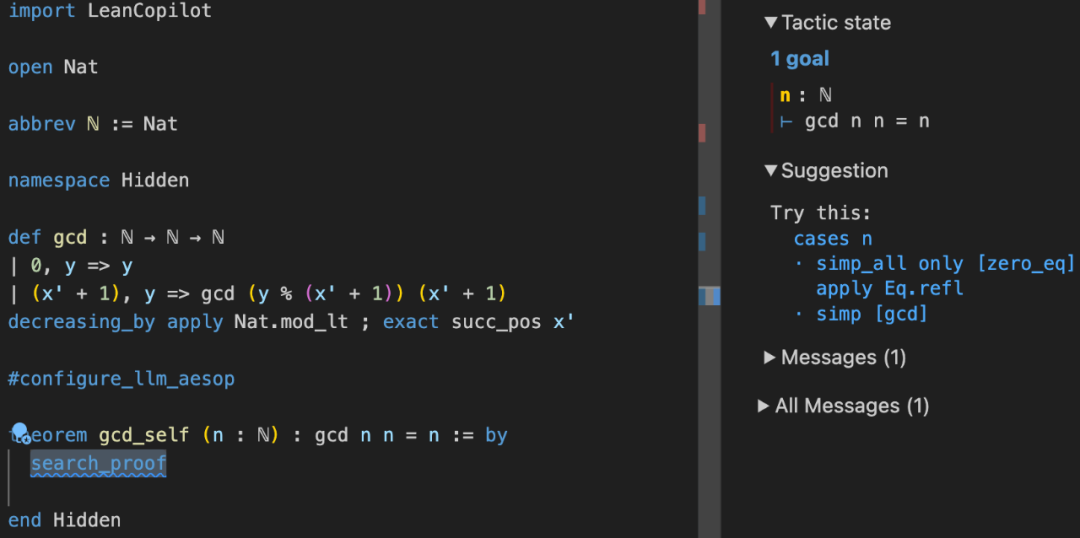
Recherchez des preuves. Utilisez search_proof pour combiner les politiques générées par LLM avec aesop (le projet d'automatisation en boîte blanche de Lean 4) afin de rechercher plusieurs preuves de politique. Une fois que vous avez trouvé la preuve, vous pouvez cliquer sur la stratégie pour l'insérer dans l'éditeur

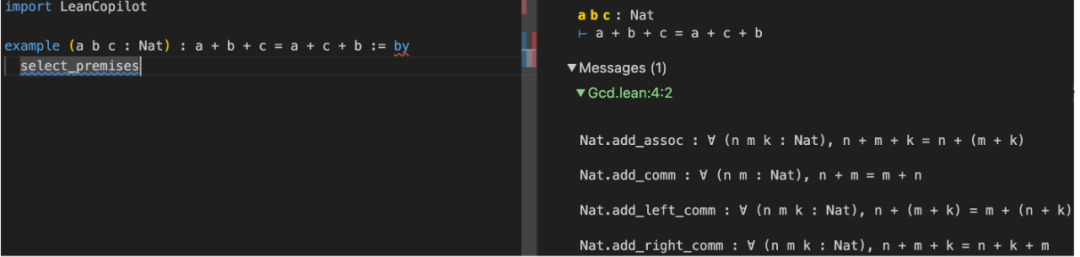
Contenu réécrit : Choisir une prémisse est une stratégie importante. Le but de cette stratégie est de récupérer une liste de locaux potentiellement utiles. Actuellement, Lean Copilot utilisera l'outil de recherche de LeanDojo pour sélectionner des locaux à partir de l'instantané fixe de Lean et mathlib4 (c'est-à-dire la bibliothèque mathématique Lean 4)

Vous pouvez exécuter LLM. Qu'il s'agisse de prouver un théorème ou d'autres raisonnements, vous pouvez exécuter un LLM en Lean. Vous pouvez exécuter n'importe quel modèle localement ou à distance (voir Bring Your Own Model)

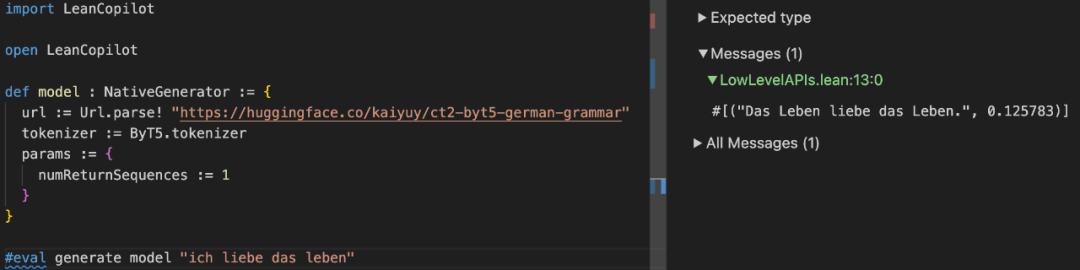
Certaines utilisations avancées sont également mentionnées dans le projet. Les lecteurs intéressés peuvent accéder au projet original pour en savoir plus.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!