
Après avoir été « approuvé » par GPT-4, Copilot a également été favorisé par Terence Tao.
Il a dit sans ambages que lors de la programmation, Copilot peut directement prédire ce qu'il fera ensuite.
Avec Copilot, la recherche est devenue plus pratique. Tao Zhexuan l'a également utilisé pour l'aider à finaliser ses derniers résultats de recherche.

Tao Zhexuan a déclaré que cette partie du journal ne comporte en réalité qu'une seule page.
Mais pour compléter cette preuve d'une page, il a écrit plus de 200 lignes de code, en utilisant le langage de programmation nouvellement appris Lean4.

La page GitHub du code public de Tao Zhexuan montre que Copilot a augmenté la vitesse d'écriture du code de plus de moitié.
Tao Zhexuan a déclaré que la raison pour laquelle il a choisi Lean4 était en raison de sa « stratégie de réécriture », qui consiste à effectuer un remplacement partiel ciblé d'une expression longue.
Par exemple, si une fonction complexe f(x) est définie, lorsque l'on veut saisir l'expression de f(114514), on peut directement "réécrire" x en 114514 à l'aide du code.
Tao Zhexuan a déclaré que cette fonctionnalité n'est pas très pratique par rapport à LaTeX qui nécessite la saisie répétée de formules.
Alors, quels nouveaux résultats la « preuve d’une page » de Tao Zhexuan nous a-t-elle apporté cette fois-ci ?
Cet article traite des problèmes liés à l'inégalité de MacLaughlin.
L'inégalité de McLaughlin est une inégalité classique en mathématiques. Elle est dérivée de la loi selon laquelle "la moyenne arithmétique des nombres réels non négatifs est supérieure ou égale à la moyenne géométrique".
1...yn est un nombre réel non négatif Pour k=1...n, la moyenne Sk est définie comme (le dénominateur est le nombre de termes dans le numérateur) :
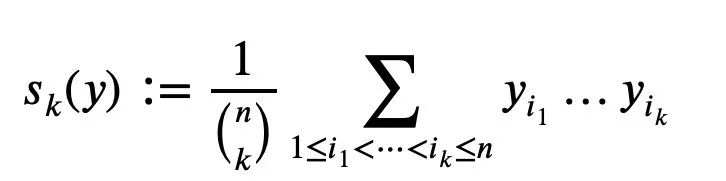 Il apparaît comme le coefficient normalisé d'un polynôme de nième degré avec racines.
Il apparaît comme le coefficient normalisé d'un polynôme de nième degré avec racines.
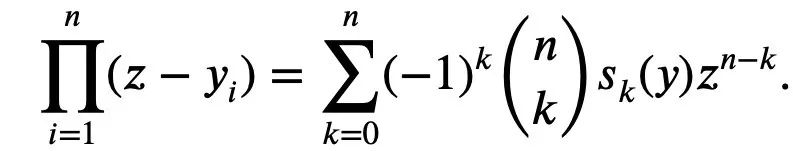 (Rappelez-vous cette formule, nous l'appelons Formule 1)
(Rappelez-vous cette formule, nous l'appelons Formule 1)
Ensuite, l'inégalité de McLaughlin peut être exprimée comme suit :
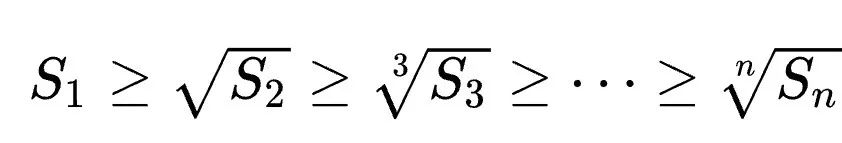 Le signe égal si et seulement si tous y
Le signe égal si et seulement si tous y
sont égaux établis. En calcul, il existe aussi une inégalité de Newton classique :
sont toutes non négatives, l'inégalité de Newton peut simplement décrire Mike L'inégalité de Laurin : Donc, pour la situation où des termes négatifs peuvent exister dans les inégalités de Newton, Tao Zhexuan a proposé un nouvel ensemble de variantes d'inégalités : Pour tout r>0 et 1≤ℓ≤n, l'équation 2 ou l'équation 3 doit être vraie. Autant construire un polynôme P(z) sur la variable complexe z : Il suffit donc d'établir une borne inférieure : Prendre la valeur absolue de P(z) puis prendre le logarithme pour obtenir : Puisque pour tout nombre réel t, t ↦ log(e t+a) est la convexité et a>0, on peut obtenir l'inégalité : Quand a=r2, t=2log yj, on peut obtenir : Le ci-dessus est le processus de preuve donné par Tao Zhexuan, cependant, lorsque le |Sn|=1 normalisé, la formule suivante est valable : En plus du "one- preuve de page" mentionné cette fois, cet article de Terence Tao a également proposé un autre nouveau théorème, c'est-à-dire pour tout 1 ≤ k ≤ ℓ≤ n. : Dans le billet de blog, Tao Zhexuan a révélé que son prochain plan est de proposent cette inégalité Version raffinée. Tao Zhexuan a déclaré que le processus de preuve sera aussi simple que la pratique et pourra être effectué avec du calcul. Cependant, il a également mentionné qu'il y aura une petite difficulté car cette partie de l'argumentation utilise des symboles asymptotiques. Attendons de voir quelle sera la nouvelle conclusion. Tao Zhexuan est un fidèle fan des outils d'IA Copilot, GPT-4 et quelques autres outils auxiliaires qu'il a recommandés. Cette fois, il a également avancé de nouvelles attentes pour le développement de grands modèles, en espérant qu'un jour le modèle puisse générer directement des variantes d'inégalité. Adresse papier : https://arxiv.org/abs/2310.05328 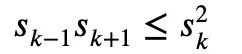 Pour tout 1≤k
Pour tout 1≤k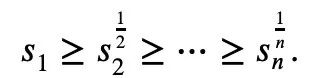 Mais si cette restriction n'est pas ajoutée, c'est-à-dire que l'existence de termes négatifs est autorisée, l'inégalité de Maclaurin ne peut pas être exprimée par l'inégalité de Newton.
Mais si cette restriction n'est pas ajoutée, c'est-à-dire que l'existence de termes négatifs est autorisée, l'inégalité de Maclaurin ne peut pas être exprimée par l'inégalité de Newton. 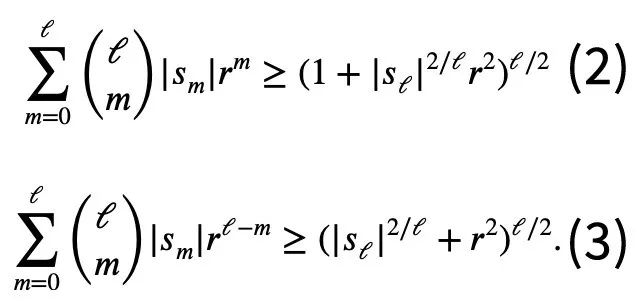 C'est ce que Tao Zhexuan veut prouver sur cette page. Le processus de preuve spécifique est le suivant :
C'est ce que Tao Zhexuan veut prouver sur cette page. Le processus de preuve spécifique est le suivant : 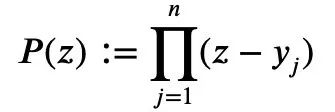 De la formule 1 précédente et l'inégalité triangulaire peuvent être obtenues :
De la formule 1 précédente et l'inégalité triangulaire peuvent être obtenues : 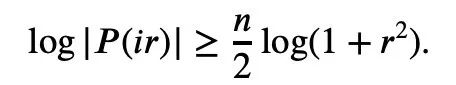
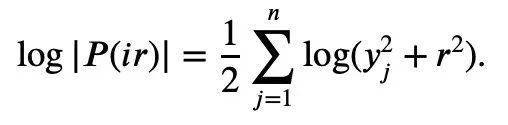
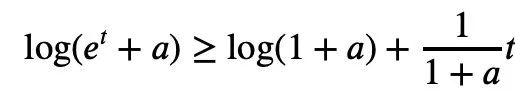
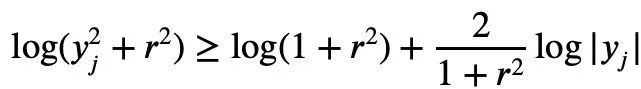
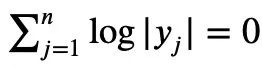
Étape suivante : créer une version raffinée
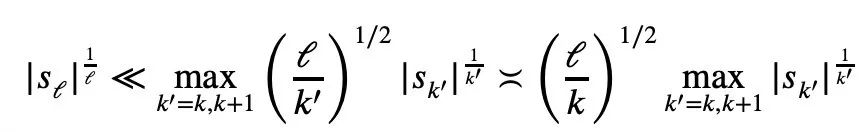

One More Thing

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 Comment gérer les caractères chinois tronqués sous Linux
Comment gérer les caractères chinois tronqués sous Linux
 Ordre recommandé pour apprendre le langage C++ et C
Ordre recommandé pour apprendre le langage C++ et C
 Comment résoudre les caractères tronqués en PHP
Comment résoudre les caractères tronqués en PHP
 Méthode de réparation des doutes sur la base de données
Méthode de réparation des doutes sur la base de données
 Solution de délai d'expiration des requêtes du serveur
Solution de délai d'expiration des requêtes du serveur
 Solution d'erreur inattendue IIS 0x8ffe2740
Solution d'erreur inattendue IIS 0x8ffe2740
 navigateur.useragent
navigateur.useragent
 Comment obtenir un jeton
Comment obtenir un jeton