
Les algorithmes sont devenus omniprésents, et il semble que pour chaque problème pouvant être exprimé en termes mathématiques précis, il existe un algorithme correspondant. Cependant, ce n'est pas le cas. En fait, certains problèmes apparemment simples ne peuvent jamais être résolus par des algorithmes. Alan Turing, un pionnier parmi les informaticiens, a prouvé un jour ce problème "incalculable" dans un article il y a près d'un siècle. le modèle mathématique computationnel qui a lancé l’informatique moderne.
Turing a démontré ce résultat révolutionnaire en utilisant une stratégie contre-intuitive : il a défini un problème, un problème qui rejette toutes les tentatives pour le résoudre. "Par exemple, si je vous demande ce que vous faites, quelle que soit votre réponse, je dirai : 'Ce que je vais faire est différent de ce que vous avez dit'", a déclaré Rahul Ilango, étudiant diplômé du MIT. informatique théorique. Contenu réécrit : Turing a démontré ce résultat révolutionnaire avec une stratégie contre-intuitive : il a défini un problème qui a résisté à toutes les tentatives pour le résoudre. "Par exemple, si je vous demande ce que vous faites, quelle que soit votre réponse, je dirai : 'Ce que je vais faire est différent de ce que vous avez dit'", a déclaré Rahul Ilango, un étudiant diplômé en informatique théorique. science au MIT
Turing's La stratégie est basée sur une méthode mathématique de longue date connue sous le nom de « preuve diagonale ». Voici une explication simplifiée de la logique derrière sa preuve
StringsLa preuve diagonale vient d'une astuce astucieuse pour résoudre un problème concernant les chaînes, où chaque bit peut avoir une valeur de 0 ou 1. La description du problème est la suivante : étant donné une liste de chaînes, toutes les chaînes de la liste ont la même longueur, comment pouvez-vous générer une nouvelle chaîne qui ne figure pas dans la liste ?
Contenu réécrit : l'une des stratégies les plus simples consiste à considérer toutes les chaînes possibles dans l'ordre. Supposons qu’il y ait cinq chaînes de cinq bits chacune. Commencez par parcourir pour vérifier si 00000 existe dans la liste. S'il n'existe pas, le problème est résolu ; s'il existe, passez à 00001 et répétez le processus. Cette approche est simple, mais lente pour les longues listes résultant de longues chaînes
Diagonal s'avère être une alternative viable pour construire progressivement des chaînes inexistantes. En commençant par le premier bit de la première chaîne de la liste, inversez-le et cela deviendra le premier bit de la nouvelle chaîne. Inversez ensuite le deuxième bit de la deuxième chaîne et utilisez-le comme deuxième bit de la nouvelle chaîne, répétez cette opération jusqu'à ce que vous atteigniez la fin de la liste. En inversant les opérations sur les bits, vous vous assurez que la nouvelle chaîne est différente de chaque chaîne de la liste d'origine d'au moins une position. (Ils forment également une diagonale dans la liste des chaînes, d'où le nom de preuve diagonale.)
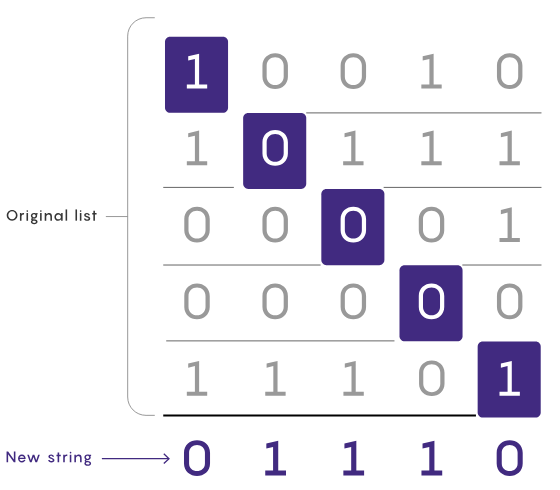 La preuve diagonale ne nécessite que de vérifier tour à tour un bit de chaque chaîne de la liste, donc généralement beaucoup plus rapide que les autres méthodes, mais sa véritable puissance réside dans sa capacité à gérer les problèmes de chaînes infiniment longues.
La preuve diagonale ne nécessite que de vérifier tour à tour un bit de chaque chaîne de la liste, donc généralement beaucoup plus rapide que les autres méthodes, mais sa véritable puissance réside dans sa capacité à gérer les problèmes de chaînes infiniment longues.
L'informaticien théorique Ryan Williams du MIT a déclaré : "Bien que les chaînes et les listes puissent être infinies, la méthode de diagonalisation est toujours efficace.
George Cantor a été le premier à exploiter cela. Un homme de pouvoir, il a été le fondateur du domaine." des mathématiques de la théorie des ensembles. En 1873, il utilise les diagonales pour montrer que certaines valeurs infinies sont plus grandes que d'autres. 60 ans plus tard, Turing a appliqué cette version de la preuve diagonale à la théorie du calcul
Les limites des algorithmesPour prouver qu'il existe une classe de problèmes mathématiques qui ne peuvent être résolus par aucun algorithme, Turing a proposé une théorie. Ce type de problème a des entrées et des sorties bien définies, mais aucun processus défini pour convertir les entrées en sorties. Turing s’est principalement concentré sur les problèmes de prise de décision et a cherché à mieux concrétiser cette tâche nébuleuse. Dans un problème de décision, l'entrée peut être n'importe quelle chaîne composée de 0 et 1, et la sortie peut être 0 ou 1
Déterminer si un nombre est premier (divisible uniquement par 1 et lui-même) est un exemple de problème de décision — — Étant donné une chaîne d'entrée représentant un nombre, la sortie correcte est 1 si le nombre est premier et 0 s'il n'est pas premier. Un autre exemple consiste à vérifier les programmes informatiques pour détecter les erreurs de syntaxe. Les chaînes d'entrée représentent le code de différents programmes - tous les programmes peuvent être représentés de cette façon car c'est ainsi qu'ils sont stockés et exécutés sur l'ordinateur - la règle est que si le code contient une erreur de syntaxe, alors affichez 1, sinon, alors sortie 0.
Seulement si un algorithme produit le résultat correct pour chaque entrée possible, on peut dire qu'il résout le problème - s'il échoue ne serait-ce qu'une seule fois, ce n'est pas un algorithme général pour résoudre le problème. Généralement, on spécifie un problème que l’on souhaite résoudre, puis on essaie de trouver un algorithme pour le résoudre. Turing a renversé cette logique lorsqu'il recherchait des problèmes insolubles : il a imaginé une liste infinie de tous les algorithmes possibles et a utilisé la diagonalisation pour construire un puzzle opposé à tous les algorithmes de la liste.
Veuillez imaginer une nouvelle question composée de 20 questions. Au lieu de partir d'un concept spécifique, le répondant propose un exemple d'insatisfaction pour chaque question tour à tour. À la fin du jeu, celui qui a répondu a décrit une proposition qui est entièrement composée des opposés de la question.
Le processus de preuve diagonale de Turing consiste à penser à chaque algorithme dans une liste infiniment longue d'algorithmes : « Un algorithme peut-il résoudre le problème que nous voulez-vous prouver que vous n'êtes pas calculable ? » C'est comme un jeu de compétition. Williams a déclaré : « Cette méthode transforme le problème initial en un « problème infini ». »
Pour gagner la partie, Turing doit concevoir une question dans laquelle la réponse donnée par chaque algorithme est négative. Cela signifie trouver l’entrée spécifique qui a fait que le premier algorithme a produit la mauvaise réponse, une autre entrée qui a fait échouer le deuxième algorithme, et ainsi de suite. Il a découvert que ces entrées spéciales utilisaient une méthode similaire à celle utilisée par Kurt Gödel il n'y a pas si longtemps lorsqu'il montrait que des affirmations autoréférentielles telles que « Cette proposition n'est pas prouvable » peuvent causer des problèmes dans les fondements des compétences mathématiques.
La clé ici est que chaque algorithme (ou programme) peut être représenté comme une chaîne de 0 et de 1. Cela signifie que, tout comme dans l’exemple du vérificateur d’erreurs, un algorithme peut prendre en entrée l’encodage d’un autre algorithme. En principe, l’algorithme pourrait même prendre son propre codage en entrée.
De cette façon, nous pouvons définir un problème non calculable, tout comme le problème mentionné dans la preuve de Turing : « Étant donné une chaîne d'entrée représentant le code d'un algorithme, lorsque le code de l'algorithme lui-même est pris en entrée, si le l'algorithme produit 0, laissez-le produire 1, sinon il produit 0. "Chaque algorithme qui tente de résoudre ce problème produira une sortie incorrecte sur au moins une entrée, celle qui correspond à son propre code. Cela signifie que ce problème anormal ne peut être résolu par aucun algorithme
Ce qui ne peut pas être prouvé est une preuve par contradiction
L’utilisation par les informaticiens des preuves diagonales ne s’arrête pas là. En 1965, Juris Hartmanis et Richard Stearns ont adapté l'argument de Turing pour montrer que tous les problèmes calculables ne sont pas égaux : certains sont intrinsèquement plus difficiles que d'autres. Ce résultat a lancé le domaine de la théorie de la complexité informatique, l'étude de la difficulté des problèmes informatiques.
Le développement de la théorie de la complexité révèle les limites de la preuve diagonale de Turing. En 1975, Baker, Gill et Solovy ont démontré que de nombreux problèmes non résolus en théorie de la complexité ne pouvaient être résolus par la seule diagonalisation. Le plus important d'entre eux est le fameux problème P/NP, qui consiste simplement à savoir si l'exactitude de la solution peut être vérifiée en temps polynomial et si elle peut être résolue en temps polynomial. La limitation de la preuve diagonale est une conséquence directe de. le haut niveau d'abstraction qui le rend si puissant. La preuve de Turing n'a abordé aucun des problèmes non calculables qui pourraient survenir dans la pratique ; les problèmes ont plutôt tendance à être abstraits. D’autres diagonales s’avèrent tout aussi éloignées du monde réel et ne peuvent donc pas résoudre les problèmes du monde réel.
Williams a déclaré : "La preuve diagonale ne touche pas directement le problème lui-même, tout comme faire une expérience avec une boîte à gants."
La tendance à la baisse de la preuve diagonale montre que la résolution du problème P/NP sera un long processus. voyage. Malgré leurs limites, les preuves diagonales restent l'un des outils clés de l'arsenal des théoriciens de la complexité. En 2011, Williams l’a combiné avec une gamme d’autres techniques pour démontrer qu’un modèle informatique restreint était incapable de résoudre certains problèmes incroyablement difficiles – un résultat qui a résolu un problème qui contrariait les chercheurs depuis 25 ans. Même si cela est loin de résoudre le problème P/NP, cela représente néanmoins un progrès significatif.
Si vous voulez prouver que quelque chose est impossible, ne sous-estimez pas le pouvoir de la négation
Lien original :Le contenu qui doit être réécrit est : https://www.quantamagazine.org/alan- turing-et-le-pouvoir-de-la-pensée-négative-20230905/
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!