
Algorithme gourmand
Applications classiques : telles que Huffman Coding, les algorithmes d'arbre couvrant minimum Prim et Kruskal et l'algorithme de chemin le plus court à source unique de Dijkstra.
Étapes d'un algorithme glouton pour résoudre les problèmes
La première étape, quand on voit ce genre de problème, il faut d'abord penser à l'algorithme glouton : pour un ensemble de données, on définit la valeur limite et la valeur attendue, et espérer en sélectionner quelques données Quand. la valeur limite est respectée. En dessous, la valeur attendue est la plus élevée.
Par analogie avec l'exemple de tout à l'heure, la valeur limite est que le poids ne peut pas dépasser 100 kg, et la valeur attendue est la valeur totale de l'article. Cet ensemble de données comprend 5 types de haricots. Nous en sélectionnons une portion qui ne pèse pas plus de 100 kg et qui a la plus grande valeur totale.
Dans la deuxième étape, nous essayons de voir si ce problème peut être résolu avec un algorithme glouton : à chaque fois, sélectionnez les données qui contribuent le plus à la valeur attendue dans la situation actuelle et contribuent dans la même mesure à la valeur limite.
Par analogie avec l'exemple de tout à l'heure, nous sélectionnons à chaque fois les haricots avec le prix unitaire le plus élevé parmi les haricots restants, c'est-à-dire les haricots qui contribuent le plus à la valeur lorsque le poids est le même.
La troisième étape, donnons quelques exemples pour voir si les résultats produits par l'algorithme glouton sont optimaux. Dans la plupart des cas, donnez simplement quelques exemples pour vérifier. Prouver strictement l’exactitude de l’algorithme glouton est très compliqué et nécessite beaucoup de raisonnement mathématique.
La principale raison pour laquelle l'algorithme glouton ne fonctionne pas est que les choix précédents affecteront les choix suivants.
Analyse pratique de l'algorithme gourmand
1. Partagez des bonbons
Nous avons m bonbons et n enfants. Nous voulons maintenant distribuer des bonbons à ces enfants, mais il y a moins de bonbons et plus d'enfants (m Nous pouvons résumer ce problème en, parmi n enfants, sélectionner quelques enfants pour distribuer des bonbons, de sorte que le nombre d'enfants satisfaits (valeur attendue) soit le plus grand. La valeur limite de ce problème est le nombre de bonbons m.
Chaque fois, nous trouvons parmi les enfants restants celui qui a la plus petite demande de taille de bonbon, puis lui donnons le plus petit bonbon parmi les bonbons restants qui peut le satisfaire. Le plan de distribution ainsi obtenu est celui de l'enfant individuel qui est. satisfait. Les options les plus nombreuses.
2. Changement de pièces
Ce problème est plus courant dans notre vie quotidienne. Supposons que nous ayons des billets de 1 yuan, 2 yuans, 5 yuans, 10 yuans, 20 yuans, 50 yuans et 100 yuans. Leurs numéros sont respectivement c1, c2, c5, c10, c20, c50 et c100. Nous devons maintenant utiliser cet argent pour payer des K yuans. Quel est le nombre minimum de billets que nous devons utiliser ?
Dans la vie, il faut d'abord payer avec celui avec la plus grande valeur nominale. Si cela ne suffit pas, continuer à utiliser celui avec la plus petite valeur nominale, et ainsi de suite, et enfin utiliser 1 yuan pour compenser le reste. Dans le cas d'une contribution de la même valeur attendue (nombre de billets), nous espérons contribuer davantage, afin que le nombre de billets puisse être réduit. C'est la solution d'un algorithme glouton.
3. Couverture par intervalles
Supposons que nous ayons n intervalles et que les extrémités de début et de fin de l'intervalle soient [l1, r1], [l2, r2], [l3, r3], ..., [ln, rn]. Nous sélectionnons une partie des intervalles parmi ces n intervalles. Cette partie de l'intervalle vérifie que les deux intervalles ne se coupent pas (les extrémités qui se croisent ne sont pas considérées comme des intersections). Combien d'intervalles peuvent être sélectionnés au maximum ?
Cette idée de traitement est utilisée dans de nombreux problèmes d'algorithmes gloutons, tels que la planification des tâches, la planification des enseignants, etc.
La solution à ce problème est la suivante : nous supposons que l'extrémité la plus à gauche de ces n intervalles est lmin et que l'extrémité la plus à droite est rmax. Ce problème équivaut à sélectionner plusieurs intervalles disjoints et à parcourir [lmin, rmax] de gauche à droite. Nous trions ces n intervalles par ordre décroissant de point final de départ petit à grand.
Chaque fois que nous sélectionnons, l'extrémité gauche ne coïncide pas avec l'intervalle précédemment couvert et l'extrémité droite est aussi petite que possible, de sorte que l'intervalle non couvert restant puisse être rendu aussi grand que possible et que davantage d'intervalles puissent être placés. Il s’agit en fait d’une méthode de sélection gourmande.
Comment implémenter le codage de Huffman à l'aide d'un algorithme glouton ?
Le codage Huffman utilise cette méthode de codage de longueur inégale pour coder les caractères. Il est nécessaire qu'entre les encodages de chaque caractère, il n'y ait aucune situation où un encodage soit le préfixe d'un autre encodage. Utilisez un encodage légèrement plus court pour les caractères qui apparaissent plus fréquemment ; utilisez un encodage légèrement plus long pour les caractères qui apparaissent moins fréquemment.
Supposons que j'ai un fichier contenant 1 000 caractères. Chaque caractère occupe 1 octet (1 octet = 8 bits). Il faut un total de 8 000 bits pour stocker ces 1 000 caractères. Existe-t-il une méthode de stockage plus économe en espace ?
Supposons que nous découvrions grâce à une analyse statistique que ces 1000 caractères ne contiennent que 6 caractères différents, en supposant qu'ils soient a, b, c, d, e, f. 3 bits binaires peuvent représenter 8 caractères différents. Par conséquent, afin de minimiser l'espace de stockage, nous utilisons 3 bits binaires pour représenter chaque caractère. Ensuite, il ne faut que 3 000 bits pour stocker ces 1 000 caractères, ce qui permet d'économiser beaucoup d'espace par rapport à la méthode de stockage d'origine. Cependant, existe-t-il une méthode de stockage plus économe en place ?
a(000), b(001), c(010), d(011), e(100), f(101)
Le codage Huffman est une méthode de codage très efficace et est largement utilisée dans la compression des données. Son taux de compression est généralement compris entre 20% et 90%.
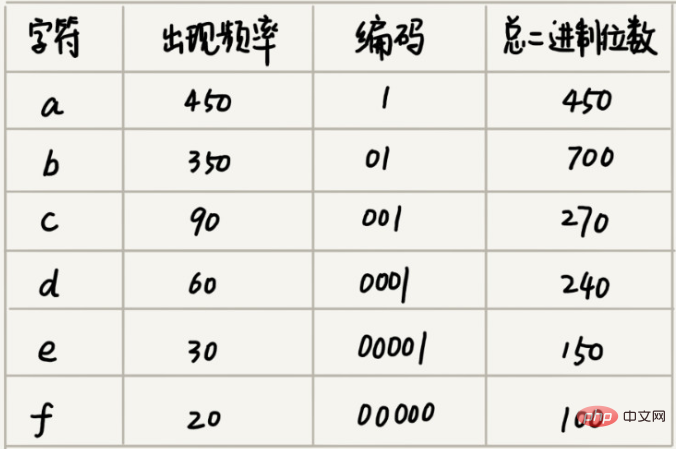
Le codage Huffman examine non seulement le nombre de caractères différents qu'il y a dans le texte, mais examine également la fréquence d'apparition de chaque caractère et sélectionne des codes de différentes longueurs en fonction de la fréquence. Le codage de Huffman tente d'utiliser cette méthode de codage de longueur inégale pour augmenter encore l'efficacité de la compression. Comment choisir des codes de longueur différents pour des caractères avec des fréquences différentes ? Selon une pensée gourmande, nous pouvons utiliser des codes légèrement plus courts pour les caractères qui apparaissent plus fréquemment ; utiliser des codes légèrement plus longs pour les caractères qui apparaissent moins fréquemment.
Les codes ne sont pas de longueur égale. Comment les lire et les analyser ?
Pour un encodage de longueur égale, il nous est très simple de décompresser. Par exemple, dans l'exemple de tout à l'heure, nous utilisons 3 bits pour représenter un caractère. Lors de la décompression, nous lisons à chaque fois les codes binaires à 3 chiffres du texte et les traduisons en caractères correspondants. Cependant, les codes de Huffman ne sont pas de longueur égale. Faut-il lire 1 bit à chaque fois, ou 2 bits, 3 bits, etc. pour la décompression ? Ce problème rend le codage de Huffman plus compliqué à décompresser. Afin d'éviter toute ambiguïté lors du processus de décompression, l'encodage Huffman nécessite qu'entre les encodages de chaque caractère, il n'y ait aucune situation où un encodage est le préfixe d'un autre encodage.
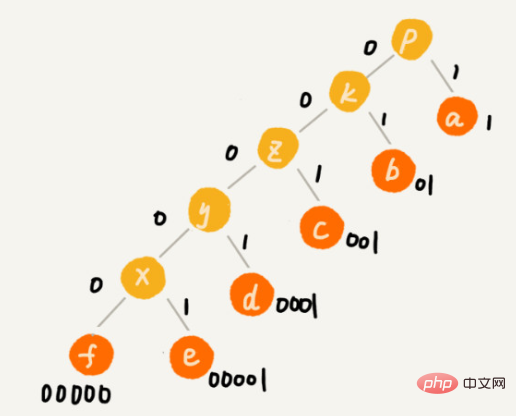
Supposons que la fréquence de ces 6 caractères de haut en bas soit a, b, c, d, e, f. Nous les encodons ainsi. L'encodage d'un caractère n'est pas le préfixe d'un autre. Lors de la décompression, nous lirons à chaque fois une chaîne binaire décompressable aussi longue que possible, donc il n'y aura pas d'ambiguïté. Après cet encodage et cette compression, ces 1000 caractères ne nécessitent plus que 2100 bits.
Bien que l'idée du codage Huffman ne soit pas difficile à comprendre, Comment encoder différents caractères avec des longueurs différentes selon la fréquence d'apparition des caractères ?
Utilisez une grande pile pour placer les personnages en fonction de la fréquence.
algorithme diviser pour régner
L'idée centrale de l'algorithme diviser pour régner est en fait quatre mots : diviser pour régner, c'est-à-dire diviser le problème d'origine en n sous-problèmes plus petits avec une structure similaire au problème d'origine. Résolvez ces sous-problèmes de manière récursive puis combinez leurs résultats pour obtenir une solution au problème d'origine.
L'algorithme diviser pour régner est une idée de résolution de problèmes, et la récursivité est une technique de programmation. En fait, les algorithmes diviser pour régner sont généralement plus adaptés à une implémentation récursive. Dans l'implémentation récursive de l'algorithme diviser pour régner, chaque niveau de récursion implique les trois opérations suivantes :
Décomposition : Décomposer le problème d'origine en une série de sous-problèmes ; 🎜🎜# Des sous-problèmes peuvent être fusionnés dans le problème d'origine, mais la complexité de cette opération de fusion ne peut pas être trop élevée, sinon elle n'aura pas pour effet de réduire la complexité globale de l'algorithme. Comment programmer pour trouver le nombre de paires ordonnées ou le nombre de paires inversées d'un ensemble de données ?
Comparez chaque nombre avec le nombre qui le suit pour voir combien sont plus petits que lui. Nous enregistrons le nombre de nombres inférieurs à k. De cette façon, après avoir examiné chaque nombre, nous résumons les valeurs k correspondant à chaque nombre. La somme finale obtenue est le nombre de paires dans l'ordre inverse. Cependant, la complexité temporelle de cette opération est O(n^2).
Nous pouvons diviser le tableau en deux moitiés, A1 et A2, calculer respectivement le nombre de paires d'ordre inverse K1 et K2 de A1 et A2, puis calculer le nombre de paires d'ordre inverse K3 entre A1 et A2. Alors le nombre de paires d’ordre inverse dans le tableau A est égal à K1+K2+K3. Avec l'aide de l'algorithme de tri par fusion
Est-il nécessaire de trier les fichiers de commande de 10 Go par montant ?
Nous pouvons d'abord scanner la commande et diviser le fichier de 10 Go en plusieurs tranches de montant en fonction du montant de la commande. Par exemple, le montant de la commande entre 1 et 100 yuans est placé dans un petit fichier, le montant de la commande entre 101 et 200 est placé dans un autre fichier, et ainsi de suite. De cette manière, chaque petit fichier peut être chargé dans la mémoire pour être trié séparément, et finalement ces petits fichiers ordonnés sont fusionnés pour obtenir les données de commande finales commandées de 10 Go.
Algorithme de retour en arrière
Scénarios d'application : recherche en profondeur, correspondance d'expressions régulières, analyse syntaxique dans les principes de compilation. De nombreux problèmes mathématiques classiques peuvent être résolus à l'aide de l'algorithme de backtracking, tels que le Sudoku, les huit dames, le sac à dos 0-1, la coloration des graphiques, le problème du voyageur de commerce, la permutation totale, etc.
L'idée de traitement du retour en arrière est quelque peu similaire à la recherche par énumération. Nous énumérons toutes les solutions et trouvons celle qui répond à nos attentes. Afin d'énumérer régulièrement toutes les solutions possibles et d'éviter les omissions et les duplications, nous divisons le processus de résolution de problèmes en plusieurs étapes. A chaque étape, nous serons confrontés à une bifurcation. Nous choisissons d'abord un chemin au hasard. Lorsque nous constatons que ce chemin ne fonctionne pas (ne répond pas à la solution attendue), nous revenons à la bifurcation précédente et. choisissez un autre chemin. Continuez à marcher.
Problème des huit reines
Nous avons un échiquier 8x8 et nous voulons y placer 8 pièces d'échecs (reines). Chaque pièce d'échecs ne peut pas avoir une autre pièce d'échecs dans la rangée, la colonne ou la diagonale.
Sac à dos 1.0-1
De nombreux scénarios peuvent être résumés dans ce modèle de problème. La solution classique à ce problème est la programmation dynamique, mais il existe également une solution simple mais moins efficace, qui est l’algorithme de backtracking dont nous parlons aujourd’hui.
Nous avons un sac à dos et le poids total du sac à dos est de Wkg. Nous avons maintenant n éléments, chacun ayant un poids différent et étant indivisible. Nous souhaitons maintenant sélectionner quelques éléments et les charger dans notre sac à dos. Comment maximiser le poids total des objets dans un sac à dos sans dépasser le poids que le sac à dos peut supporter ?
Pour chaque article, il y a deux options, le mettre dans le sac à dos ou ne pas le mettre dans le sac à dos. Pour n éléments, il existe 2 ^ n façons de les installer. Supprimez ceux dont le poids total dépasse Wkg et sélectionnez celui dont le poids total est le plus proche de Wkg parmi les méthodes d'installation restantes. Mais comment énumérer de manière exhaustive ces 2^n manières de faire semblant, sans répétition ?
Méthode de retour en arrière : Nous pouvons organiser les éléments dans l'ordre, et l'ensemble du problème est décomposé en n étapes, et chaque étape correspond à la façon de choisir un élément. Traitez d'abord le premier élément, choisissez de le charger ou non, puis traitez les éléments restants de manière récursive.
Programmation dynamique
La programmation dynamique est plus adaptée pour résoudre des problèmes optimaux, tels que trouver des valeurs maximales, des valeurs minimales, etc. Cela peut réduire considérablement la complexité du temps et améliorer l’efficacité de l’exécution du code.
Problème de sac à dos 0-1
Pour un ensemble d'articles indivisibles de poids différents, nous devons en sélectionner quelques-uns à mettre dans le sac à dos. En partant du principe que la limite de poids maximum du sac à dos est respectée, quel est le poids total maximum des articles dans le sac à dos ?
Pensée :
(1) Divisez l'ensemble du processus de résolution en n étapes, et chaque étape décidera s'il faut mettre un article dans le sac à dos. Une fois que chaque article a été décidé (à mettre dans le sac à dos ou à ne pas mettre dans le sac à dos), le poids des articles dans le sac à dos aura de nombreuses situations, c'est-à-dire qu'il atteindra de nombreux états différents, qui correspondent à l'arbre récursif, c'est-à-dire qu'il existe de nombreux nœuds différents.
(2) Nous fusionnons les états répétés (nœuds) de chaque couche, enregistrons uniquement les différents états, puis dérivons l'ensemble d'états de la couche suivante en fonction de l'ensemble d'états de la couche précédente. Nous pouvons fusionner les états répétés de chaque couche pour garantir que le nombre d'états différents dans chaque couche ne dépassera pas w (w représente le poids transporté par le sac à dos), qui est de 9 dans l'exemple.
Divisez n étapes. Chaque étape est dérivée en fonction de l'étape précédente et avance dynamiquement pour éviter les calculs répétés.
La complexité temporelle de l'utilisation de l'algorithme de retour en arrière pour résoudre ce problème est O(2^n), qui est exponentielle. Alors, quelle est la complexité temporelle de la solution de programmation dynamique ?
La partie la plus longue est la boucle for à deux niveaux dans le code, donc la complexité temporelle est O(n*w). n représente le nombre d'articles et w représente le poids total que le sac à dos peut supporter. Nous devons demander un tableau bidimensionnel supplémentaire de n fois w+1, ce qui consomme beaucoup d'espace. On dira donc parfois que la programmation dynamique est une solution qui échange de l’espace contre du temps.
0-1 Version améliorée du problème du sac à dos
Pour un ensemble d'articles indivisibles de poids et de valeurs différents, nous choisissons de mettre certains articles dans un sac à dos en partant du principe que la limite de poids maximale du sac à dos est respectée, quelle est la valeur totale maximale des articles qui peuvent être. chargé dans le sac à dos ?
Quels types de problèmes peuvent être résolus par la programmation dynamique ?
Trois caractéristiques d'un seul modèle
Un modèle : modèle de solution optimale de prise de décision en plusieurs étapes
Trois fonctionnalités :
Sous-structure optimale, la solution optimale du problème contient la solution optimale du sous-problème Aucune séquelle, le premier sens est que lors de la dérivation du statut des étapes ultérieures, nous ne nous soucions que des étapes précédentes La valeur d'état de , ne se soucie pas de la façon dont cet état est dérivé étape par étape. Le deuxième sens est qu’une fois que le statut d’une certaine étape est déterminé, il ne sera pas affecté par les décisions des étapes ultérieures. (Ce dernier n'affecte pas le précédent.) Des sous-problèmes répétés, des séquences de décision différentes, peuvent produire des états répétés lorsqu'ils atteignent un certain même stade. Résumé de deux idées de résolution de problèmes de programmation dynamique
1. Méthode de la table de transition d'état
Généralement, les problèmes qui peuvent être résolus par programmation dynamique peuvent être résolus par recherche par force brute à l'aide de l'algorithme de backtracking. Dessinez l'arbre de récursivité. À partir de l'arbre de récursivité, nous pouvons facilement voir s'il existe des sous-problèmes répétés et comment les sous-problèmes répétés sont générés.
Après avoir trouvé le sous-problème répété, nous avons deux façons de le résoudre. La première consiste à utiliser directement la méthode de retour en arrière et de « mémo » pour éviter les sous-problèmes répétés. En termes d'efficacité d'exécution, cela n'est pas différent de l'idée de solution de programmation dynamique. La deuxième méthode consiste à utiliser la programmation dynamique, la méthode de la table de transition d'état.
Dessinons d’abord un tableau de statut. Les tables d'états sont généralement bidimensionnelles, vous pouvez donc les considérer comme un tableau bidimensionnel. Parmi eux, chaque état contient trois variables, lignes, colonnes et valeurs de tableau. Nous remplissons chaque état du tableau d'état par étapes selon le processus de prise de décision, d'avant en arrière, et selon la relation récursive. Enfin, nous traduisons ce processus de remplissage de formulaire récursif en code, qui est du code de programmation dynamique.
nécessite la représentation de nombreuses variables, et la table d'état correspondante peut être de grande dimension, comme en trois dimensions ou en quatre dimensions. À l’heure actuelle, nous ne sommes pas en mesure d’utiliser la méthode des tables de transition d’état pour le résoudre. D'une part, c'est parce que les tableaux de transition d'état de grande dimension sont difficiles à dessiner et à représenter, et d'autre part, c'est parce que le cerveau humain n'est vraiment pas doué pour penser aux choses de grande dimension.
2. Méthode d'équation de transition d'état
Nous devons analyser comment un certain problème peut être résolu de manière récursive à travers des sous-problèmes, ce qu'on appelle la sous-structure optimale. Sur la base de la sous-structure optimale, écrivez une formule récursive, qui est ce qu'on appelle l'équation de transition d'état. Avec l’équation de transition d’état, l’implémentation du code est très simple. Généralement, nous avons deux méthodes d'implémentation de code, l'une est récursion plus "mémo" et l'autre est récursivité itérative.
min_dist(i, j) = w[i][j] + min(min_dist(i, j-1), min_dist(i-1, j))
Je tiens à souligner que tous les problèmes ne conviennent pas aux deux idées de résolution de problèmes. Certains problèmes peuvent être plus clairs avec la première façon de penser, et certains problèmes peuvent être plus clairs avec la deuxième façon de penser. Par conséquent, vous devez considérer le problème spécifique pour décider quelle méthode de résolution de problèmes utiliser. Méthode de la table de transition d'étatL'idée de résolution de problèmes peut être résumée grossièrement comme suit : Mise en œuvre de l'algorithme de retour en arrière - Définir l'état - Dessiner l'arbre de récursion - Rechercher les sous-problèmes en double - Dessiner la table de transition d'état - Remplissez le tableau en fonction à la relation de récursion - Traduisez le processus de remplissage de table en code . L'idée générale de la méthode de l'équation de transition d'état peut être résumée comme suit : Trouver la sous-structure optimale - écrire l'équation de transition d'état - traduire l'équation de transition d'état en code.
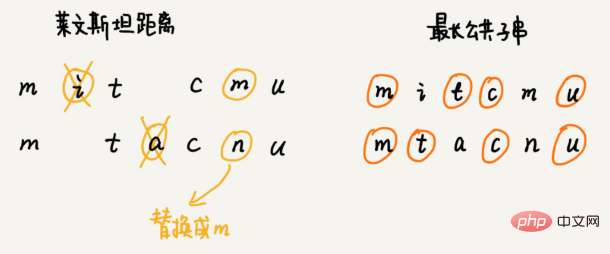
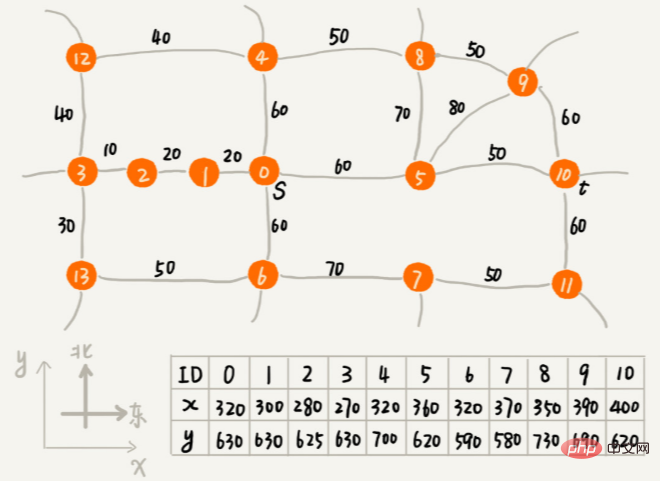
Comment quantifier la similarité de deux chaînes ? Distance d'édition fait référence au nombre minimum d'opérations d'édition requises pour convertir une chaîne en une autre chaîne (comme l'ajout d'un caractère, la suppression d'un caractère, le remplacement d'un caractère). Plus la distance d’édition est grande, plus la similarité entre les deux chaînes est faible ; à l’inverse, plus la distance d’édition est petite, plus la similarité entre les deux chaînes est grande. Pour deux chaînes identiques, la distance d'édition est de 0. Il existe de nombreuses méthodes de calcul différentes pour la distance d'édition, les plus connues sont Distance de Levenshtein et Longueur de sous-chaîne commune la plus longue. Parmi eux, la distance de Levinstein permet trois opérations d'édition d'ajout, de suppression et de remplacement de caractères, et la longueur de la sous-chaîne commune la plus longue n'autorise que deux opérations d'édition d'ajout et de suppression de caractères. La distance de Lewenstein et la plus longue longueur de sous-chaîne commune analysent la similitude des chaînes sous deux perspectives complètement opposées. La taille de la distance de Levenstein représente la différence entre deux chaînes ; et la taille de la sous-chaîne commune la plus longue représente la similitude entre deux chaînes. La distance de Levenstein entre deux chaînes mitcmu et mtacnu est de 3, et la longueur de la sous-chaîne commune la plus longue est de 4. Comment calculer la distance de Levenstein par programme ? Cette question consiste à trouver le nombre minimum de modifications requises pour changer une chaîne en une autre chaîne. L'ensemble du processus de résolution implique plusieurs étapes de prise de décision. Nous devons examiner tour à tour si chaque caractère d'une chaîne correspond aux caractères d'une autre chaîne, comment le traiter s'il correspond et comment le traiter s'il ne correspond pas. . Par conséquent, ce problème est conforme au modèle de solution optimale de prise de décision en plusieurs étapes. Algorithme recommandé Utilise la distance des vecteurs pour trouver la similitude. Recherche : Comment utiliser l'algorithme de recherche A* pour implémenter la fonction de recherche de chemin dans le jeu ? Alors, comment trouver rapidement un itinéraire sous-optimal proche de l'itinéraire le plus court ? Cet algorithme de planification de chemin rapide est l'algorithme A* que nous allons apprendre aujourd'hui. En fait, l'algorithme A* est une optimisation et une transformation de l'algorithme de Dijkstra. Estimez approximativement la longueur du chemin entre le sommet et le point final à travers la distance en ligne droite entre le sommet et le point final, qui est la distance euclidienne (remarque : la longueur du chemin et la distance en ligne droite sont deux concepts) Ceci la distance est enregistrée sous la forme h(i) (i représente le numéro de ce sommet), le nom professionnel est fonction heuristique (fonction heuristique) Parce que la formule de calcul de la distance euclidienne impliquera le calcul fastidieux du signe racine , donc , nous utilisons généralement une autre formule de calcul de distance plus simple, à savoir la distance de Manhattan (distance de Manhattan) La distance de Manhattan est la somme des distances entre les coordonnées horizontales et verticales entre deux points. Le processus de calcul implique uniquement l'addition, la soustraction et l'inversion des bits de signe, il est donc plus efficace que la distance euclidienne. int hManhattan(Vertex v1, Vertex v2) { // Le sommet représente le sommet, qui est défini plus tard
Retour Math.abs(v1.x - v2.x) + Math.abs(v1.y - v2.y);
}
f(i)=g(i)+h(i), la longueur du trajet g(i) entre le sommet et le point de départ, et la longueur estimée du trajet du sommet au point final h(i). Le nom professionnel de f(i) est La méthode est la fonction d'évaluation. Un algorithme* est une simple modification de l'algorithme de Dijkstra. Le plus petit f(i) est répertorié en premier. Il existe trois différences principales entre celui-ci et l'implémentation du code de l'algorithme de Dijkstra : La façon dont la file d'attente prioritaire est construite est différente. L'algorithme A* construit une file d'attente prioritaire basée sur la valeur f (c'est-à-dire f(i)=g(i)+h(i) que nous venons de mentionner), tandis que l'algorithme Dijkstra construit une file d'attente prioritaire basée sur la valeur dist ( c'est-à-dire le g que nous venons de mentionner (i)) pour construire une file d'attente prioritaire ; Un algorithme* mettra à jour la valeur f de manière synchrone lors de la mise à jour de la valeur de distribution du sommet Les conditions pour la fin de la boucle sont ; également différent. L'algorithme de Dijkstra se termine lorsque le point final est retiré de la file d'attente, et l'algorithme A* se termine une fois que le parcours atteint le point final. 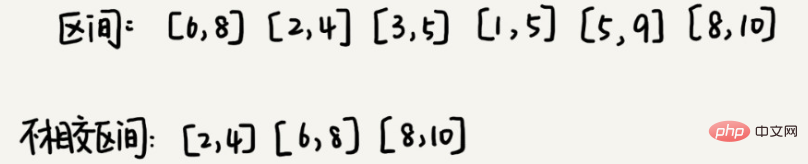
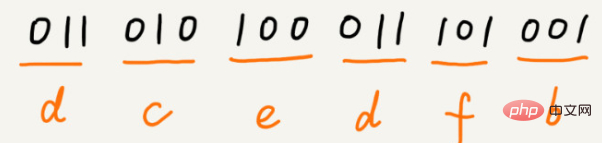
a une condition de terminaison de décomposition, c'est-à-dire que lorsque le problème est suffisamment petit, il peut être résolu directement ;#🎜🎜 #

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!