Utiliser Python pour implémenter le chiffrement et le déchiffrement RSA

J'ai vu hier un article en anglais [1], montrant comment utiliser Python pour implémenter l'algorithme RSA. La logique du code est la même que celle de l'article précédent Comprendre l'algorithme RSA. Les amis qui ne sont pas familiers avec RSA peuvent lire l'article. Comprendre l'algorithme RSA, qui explique ce qu'est RSA, les principes mathématiques de RSA, et donne un exemple simple. On peut dire que c'est l'article le plus simple pour comprendre RSA sur Quanzhihu (cela vient des commentaires des lecteurs).

J'ai exécuté le code fourni en anglais et j'ai découvert qu'il ne pouvait pas crypter le chinois. J'ai donc modifié les fonctions de cryptage et de décryptage pour prendre en charge le cryptage et le décryptage du chinois. L'article d'aujourd'hui explique comment utiliser Python pour implémenter le processus de cryptage et de déchiffrement RSA afin de vous aider à établir une compréhension intuitive de RSA. L'algorithme de génération de nombres premiers aléatoires dans le code mérite également d'être appris.

0. Démonstration de l'effet

Jetons d'abord un coup d'œil à l'effet.

Texte original : "Il y a une taupe, mettez fin à la transaction"

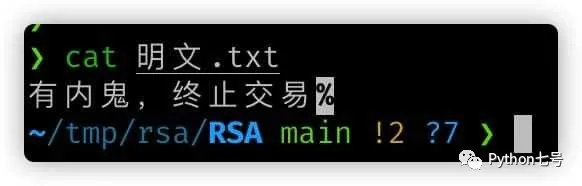
Le texte chiffré ne peut pas être déchiffré du tout :

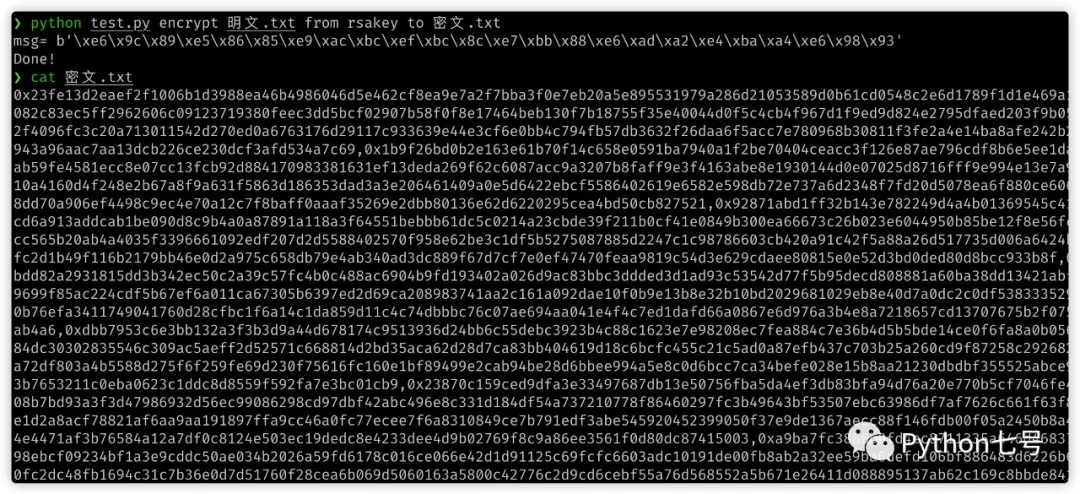
Après le décryptage :

Code complet du compte public "Python Seven" a répondu "rsa" Get.

1. Génération de paires de clés

Idées :

1) Trouvez au hasard deux nombres premiers (nombres premiers) p et q Plus p et q sont grands, plus ils sont sûrs. Ici, nous choisissons un nombre premier de 1024 bits :

p = genprime(1024)
q = genprime(1024)

genprime( ) Ne parlons pas du processus d'implémentation de la fonction.

2) Calculez leur produit n = p * q et la fonction d'Euler lambda_n.

n = p * q
lambda_n = (p - 1) * (q - 1)

3) Sélectionnez au hasard un entier e, à condition que 1 < e < lambda_n, et e et lambda_n soient relativement premiers. Par exemple, si vous sélectionnez 35537, 35537 n'a que 16 bits et doit être plus petit que lambda_n. < e < lambda_n，且 e 与 lambda_n 互质。比如选择 35537，35537 只有 16 位，必然小于 lambda_n。

e = 35537

4) Trouvez un entier d tel que le reste de e * d divisé par lambda_n soit 1, et renvoyez la paire de clés.

d = eucalg(e, lambda_n)[0]
if d < 0: d += lambda_n
return (d, n), (e, n)

eucalg L'implémentation de la fonction sera discutée plus tard.

À ce stade, la fonction de génération de paire de clés est la suivante :

def create_keys():
 p = genprime(1024)
 q = genprime(1024)
 n = p * q
 lambda_n = (p - 1) * (q - 1)
 e = 35537
 d = eucalg(e, lambda_n)[0]
 if d < 0: d += lambda_n
 return (d, n), (e, n)

2. Mise en œuvre du cryptage et du déchiffrement

Le processus de cryptage et de déchiffrement est le même, cryptage à clé publique, déchiffrement à clé privée, et vice versa, privé. cryptage par clé, déchiffrement par clé publique, mais le premier est appelé cryptage et le second est appelé signature.

L'implémentation spécifique de la fonction est la suivante :

def encrypt_data(data,key):
e_data = []
for d in data:
 e = modpow(d, key[0], key[1]) 
 e_data.append(e)
return e_data

## 加密和解密的逻辑完全一样
decrypt_data = encrypt_data

La fonction modpow est utilisée ici, qui est utilisée pour calculer la formule b^e % n = r.

• S'il s'agit d'un processus de cryptage, alors b est le texte en clair, (n,e) est la clé publique et r est le texte chiffré.
• S'il s'agit d'un processus de décryptage, alors b est le texte chiffré, (n, d) est la clé privée et r est le fameux texte.

modpow est défini comme suit :

def modpow(b, e, n):
 # find length of e in bits
 tst = 1
 siz = 0
 while e >= tst:
tst <<= 1
siz += 1
 siz -= 1
 # calculate the result
 r = 1
 for i in range(siz, -1, -1):
r = (r * r) % n
if (e >> i) & 1: r = (r * b) % n
 return r

3. Fonction de génération de nombres premiers aléatoires

Fonction de génération de nombres premiers aléatoires, qui utilise la multiplication matricielle et la séquence de Fibonacci, qui montre l'importance des mathématiques pour les algorithmes.

# matrix multiplication
def sqmatrixmul(m1, m2, w, mod):
 mr = [[0 for j in range(w)] for i in range(w)]
 for i in range(w):
for j in range(w):
 for k in range(w):
mr[i][j] = (mr[i][j] + m1[i][k] * m2[k][j]) % mod
 return mr

# fibonacci calculator
def fib(x, mod):
 if x < 3: return 1
 x -= 2
 # find length of e in bits
 tst = 1
 siz = 0
 while x >= tst:
tst <<= 1
siz += 1
 siz -= 1
 # calculate the matrix
 fm = [
# function matrix
[0, 1],
[1, 1]
 ]
 rm = [
# result matrix
# (identity)
[1, 0],
[0, 1]
 ]
 for i in range(siz, -1, -1):
rm = sqmatrixmul(rm, rm, 2, mod)
if (x >> i) & 1:
 rm = sqmatrixmul(rm, fm, 2, mod)

 # second row of resulting vector is result
 return (rm[1][0] + rm[1][1]) % mod

def genprime(siz):
 while True:
num = (1 << (siz - 1)) + secrets.randbits(siz - 1) - 10;
# num must be 3 or 7 (mod 10)
num -= num % 10
num += 3 # 3 (mod 10)
# heuristic test
if modpow(2, num - 1, num) == 1 and fib(num + 1, num) == 0:
 return num
num += 5 # 7 (mod 10)
# heuristic test
if modpow(2, num - 1, num) == 1 and fib(num + 1, num) == 0:
 return num

4. Implémentation de la fonction eucalg

L'essence de la fonction est de trouver la solution de l'équation linéaire suivante à deux variables :

e * x - lambda_n * y =1

Code spécifique :

def eucalg(a, b):
 # make a the bigger one and b the lesser one
 swapped = False
 if a < b:
a, b = b, a
swapped = True
 # ca and cb store current a and b in form of
 # coefficients with initial a and b
 # a' = ca[0] * a + ca[1] * b
 # b' = cb[0] * a + cb[1] * b
 ca = (1, 0)
 cb = (0, 1)
 while b != 0:
# k denotes how many times number b
# can be substracted from a
k = a // b
# swap a and b so b is always the lesser one
a, b, ca, cb = b, a-b*k, cb, (ca[0]-k*cb[0], ca[1]-k*cb[1])
 if swapped:
return (ca[1], ca[0])
 else:
return ca

5. :

1), Générez la clé

python test.py make-keys rsakey

La clé publique est stockée dans rsakey.pub et la clé privée est stockée dans rsakey.priv

2), cryptez le contenu du fichier

S'il y a un fichier en texte brut .txt :

python test.py encrypt 明文.txt from rsakey to 密文.txt

générera le texte chiffré .txt

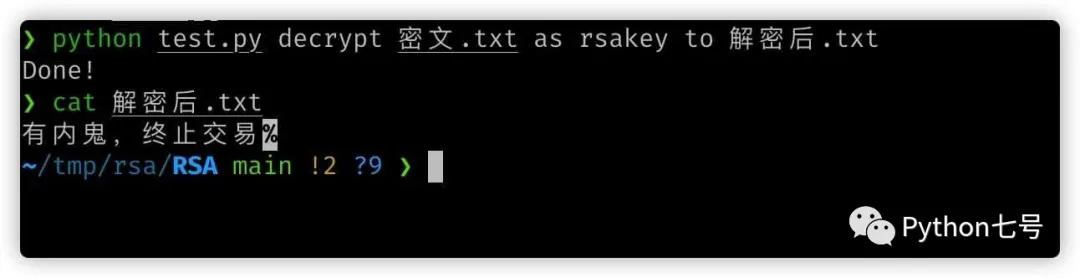
3. Décrypter le contenu du fichier

S'il existe un fichier ciphertext.txt :

python test.py decrypt 密文.txt as rsakey to 解密后.txt

générera le .txt déchiffré

Mots finaux

Cet article partage un simple implémentation de l'algorithme RSA en Python, qui peut aider à comprendre l'algorithme RSA.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!