Comment le ML fait-il des découvertes scientifiques ? La thèse de doctorat de l'Université d'Oxford de 268 pages détaille la connotation de l'apprentissage automatique scientifique

L'apprentissage automatique (ML) a provoqué un changement fondamental dans la façon dont nous pratiquons la science, nombre de personnes faisant désormais de l'apprentissage à partir des données un axe de leurs recherches. À mesure que la complexité des questions scientifiques que nous souhaitons étudier augmente et que la quantité de données générées par les expériences scientifiques actuelles augmente, le ML contribue à automatiser, accélérer et améliorer les flux de travail traditionnels. À l’avant-garde de cette révolution se trouve un domaine appelé Scientific Machine Learning (SciML). L'objectif central de SciML est d'intégrer plus étroitement les connaissances scientifiques existantes avec le ML, en générant de puissants algorithmes de ML qui s'appuient sur nos connaissances antérieures.

Adresse de papier: https://ora.ox.ac.uk/objects/uuid:b790477c-771f-4926-99c6-d2f9d248cb23

Le principe scientifique intégrant des approches de ML, les attentes grandissent quant à la capacité de SciML à résoudre certains des plus grands défis scientifiques. Cependant, le domaine est en plein essor et de nombreuses questions se posent encore. Une question majeure est de savoir si les méthodes SciML peuvent être étendues à des problèmes réels plus complexes. De nombreuses recherches SciML en sont au stade de la validation de principe, où la technologie est testée sur des problèmes simples et réduits. Cependant, comprendre leur évolutivité à des problèmes plus complexes est essentiel pour leur application généralisée. Cette question est la question centrale de cet article.

Tout d'abord, un certain nombre de méthodes d'apprentissage automatique basées sur la physique sont conçues et leurs performances et leur évolutivité sont évaluées pour trois études de cas complexes, réelles et spécifiques à un domaine de la science lunaire et de la géophysique. Deuxièmement, l'évolutivité des réseaux de neurones basés sur la physique, une méthode SciML à usage général populaire, pour résoudre des équations différentielles avec de grandes régions et des solutions haute fréquence est évaluée et améliorée. Les observations communes de ces études sont discutées et les avantages significatifs ainsi que les limites potentielles sont identifiés, soulignant l'importance de concevoir des techniques SciML évolutives.

Introduction

L'apprentissage automatique (ML) a provoqué une révolution dans le domaine scientifique. Traditionnellement, la recherche scientifique s’articule autour de la théorie et de l’expérience : on propose une théorie élaborée à la main et bien définie, puis on l’affine continuellement à l’aide de données expérimentales et on l’analyse pour faire de nouvelles prédictions. Mais aujourd’hui, de nombreuses personnes placent l’apprentissage à partir des données au cœur de leurs recherches. Ici, un modèle du monde est appris à partir de données via des algorithmes ML, et la théorie existante n'est pas nécessaire. Ce changement se produit pour diverses raisons.

Premièrement, le domaine du ML a connu une croissance exponentielle au cours de la dernière décennie, et le principal moteur de cette poussée est souvent attribué à la percée de l'apprentissage profond [Goodfellow et al., 2016]. Des découvertes importantes telles que l'utilisation de conceptions de réseaux plus approfondies et de meilleurs algorithmes de formation, ainsi que la disponibilité d'architectures informatiques plus puissantes, ont conduit à des améliorations rapides des performances des techniques d'apprentissage profond sur un large éventail de problèmes [Dally et al., 2021] . Les algorithmes modernes de ML sont désormais capables d'apprendre et de résoudre des tâches incroyablement complexes, depuis les voitures autonomes [Schwarting et al., 2018] jusqu'à battre des joueurs de Go de classe mondiale [Silver et al., 2018].

Parallèlement à ces avancées, les expériences scientifiques d’aujourd’hui génèrent de plus en plus de données et étudient des phénomènes de plus en plus complexes [Baker et al., 2019, Hey et al., 2020]. Analyser et théoriser toutes ces données devient rapidement impossible pour les humains et nos flux de travail traditionnels, et bientôt les expériences scientifiques pourraient bien être limitées par leur capacité à extraire des informations à partir des données dont elles disposent déjà, plutôt que de celles qu'elles peuvent collecter. et coll., 2019]. Compte tenu des outils puissants que le ML peut fournir, de nombreux chercheurs se tournent vers le ML pour automatiser, accélérer et améliorer les flux de travail traditionnels. Au cours de la dernière décennie, la combinaison de nouveaux algorithmes de ML et de la disponibilité des données a conduit à des avancées scientifiques majeures. Par exemple, le ML a été utilisé pour prédire les structures des protéines avec plus de précision que jamais [Jumper et al., 2021], synthétiser la parole à partir de l'activité neuronale [anummanchipalli et al., 2019] et améliorer les simulations de systèmes quantiques à N corps [ Carleo et Troyer, 2017]. En fait, les algorithmes modernes de ML sont désormais appliqués à presque tous les aspects de la science, et l'une des questions de recherche déterminantes de cette époque est devenue : « Résoudre le problème X et appliquer le ML », suivi de résultats intéressants et souvent passionnants.

Cependant, malgré ces avancées, diverses lacunes du ML, notamment des algorithmes d'apprentissage profond, se sont matérialisées dans le domaine du ML. Par exemple, malgré leur capacité à apprendre des phénomènes très complexes, les réseaux neuronaux profonds sont souvent considérés comme des « boîtes noires » avec un manque de compréhension de la manière dont ils représentent et raisonnent sur le monde. Cette ininterprétabilité est un problème critique, en particulier pour les applications critiques pour la sécurité qui nécessitent une démonstration de prédictions de réseau [Gilpin et al., 2019, Castelvecchi, 2016]. De plus, il existe peu de conseils théoriques sur la manière de concevoir des algorithmes d’apprentissage profond adaptés à des tâches spécifiques. Le choix de l'architecture de réseau neuronal profond est largement empirique, bien que les domaines du méta-apprentissage et de la recherche d'architecture neuronale commencent à proposer des approches plus automatisées [Elsken et al., 2019, Hospedales et al., 2021]. Enfin, bien que les réseaux de neurones profonds soient très expressifs, ils sont limités par les données d’entraînement et fonctionnent souvent mal en dehors de la distribution d’entraînement. L'apprentissage de modèles généralisables du monde qui fonctionnent bien sur de nouvelles tâches est une caractéristique clé des systèmes d'intelligence artificielle (IA) plus généraux et un défi majeur dans le domaine du ML [Bengio et al., 2021].

Lorsqu'ils utilisent le ML dans des problèmes scientifiques, les chercheurs commencent à rencontrer ces limitations [Ourmazd, 2020, Forde et Paganini, 2019]. Compte tenu des faibles capacités de généralisation des réseaux de neurones profonds, une question clé est de savoir s’ils « apprennent » réellement les principes scientifiques. Une bonne théorie scientifique est censée faire des prédictions nouvelles et précises en dehors des données expérimentales, mais les réseaux neuronaux profonds ont du mal à faire des prédictions précises en dehors des données d'entraînement. Même si un réseau peut faire des prédictions fiables, en extraire des informations scientifiques significatives peut s’avérer difficile étant donné leur caractère ininterprétable.

Un autre problème majeur est que de nombreux flux de travail d'apprentissage automatique actuels remplacent complètement les modèles scientifiques traditionnels par des modèles appris. Bien que cela puisse être utile, ces méthodes purement basées sur les données « jettent » une grande partie de nos connaissances scientifiques antérieures.

Le point important est que pour de nombreux problèmes, il existe une théorie existante sur laquelle s'appuyer plutôt que de partir de zéro. Dans un domaine traditionnellement basé sur une interaction étroite entre théorie explicite et expérience, certains soutiennent que les limitations ci-dessus rendent les méthodes actuelles de ML inacceptables. Ces préoccupations ont stimulé la formation d'un nouveau domaine en croissance rapide appelé Scientific Machine Learning (SciML) [Baker et al., 2019, Karniadakis et al., 2021, Willard et al., 2020, Cuomo et al., 2022, Arridge et al., 2019, Karpatne et al., 2017a]. L'objectif de SciML est de fusionner les connaissances scientifiques existantes et le ML pour générer des algorithmes de ML plus nuancés qui s'appuient sur nos connaissances antérieures, comme le montre la figure 1.1. L’argument clé dans ce domaine est qu’en procédant ainsi, nous finirons par disposer de méthodes plus puissantes pour mener des recherches scientifiques. Les méthodes traditionnelles et les méthodes ML présentent chacune des avantages et des inconvénients, et une combinaison des deux peut être plus efficace que l’une ou l’autre. Par exemple, lors de l'assimilation de données (comme dans les modèles climatiques), les modèles physiques traditionnels peuvent être utilisés pour fournir des connaissances préalables, tandis que le ML peut être utilisé pour tenir compte des dépendances des données et d'autres phénomènes physiques inconnus.

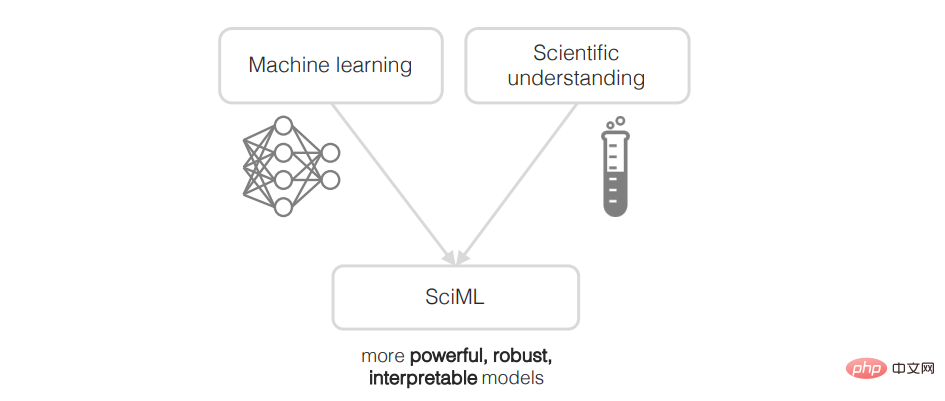
Figure 1.1 : Aperçu de l'apprentissage automatique scientifique (SciML). SciML vise à intégrer étroitement le ML aux connaissances scientifiques afin de générer des méthodes de ML plus puissantes, robustes et interprétables pour la recherche scientifique.

Les attentes dans ce domaine augmentent rapidement, et un grand nombre de méthodes et de nombreuses stratégies innovantes sont actuellement proposées et étudiées pour intégrer les connaissances scientifiques dans le ML. Ces méthodes vont des tâches scientifiques prévues (telles que la simulation, l'inversion et la découverte d'équations gouvernantes) à différentes manières d'incorporer des principes scientifiques (telles que l'architecture de réseaux neuronaux profonds, leurs fonctions de perte et l'utilisation de modèles hybrides), et des méthodes scientifiques. La mesure dans laquelle les principes sont imposés (par exemple, par le biais de contraintes strictes ou souples). Nous reviendrons sur ces méthodes en détail dans le chapitre 2. De nombreuses méthodes utilisent des idées issues de la physique pour éclairer leurs algorithmes de ML dans un sous-domaine de SciML appelé apprentissage automatique informé physiquement (PIML) [Karniadakis et al., 2021].

Jusqu'à présent, SciML a connu un premier succès. Cela nous aide à effectuer des simulations puissantes [Raissi al., 2019], à découvrir les équations régissant des systèmes physiques complexes [Kutz et Brunton, 2022] et à inverser avec précision les paramètres fondamentaux dans les problèmes d'inversion [Arridge et al., 2019] et à intégrer de manière transparente flux de travail traditionnels avec des composants appris dans un large éventail de domaines [Rackauckas et al., 2020, Thuerey et al., 2021]. Malgré ses débuts prometteurs, le domaine de SciML en est encore à ses balbutiements et de nombreuses questions importantes se posent, telles que : comment devrions-nous mettre en œuvre les principes scientifiques ? Comment devrions-nous équilibrer le manque d'interprétabilité des modèles basés sur les données avec la clarté de la théorie existante ? Existe-t-il une technologie SciML globale qui peut être appliquée dans toutes les disciplines scientifiques ? SciML peut-il fournir de nouvelles perspectives et idées pour le domaine du ML ? Dans quelle mesure la technologie SciML est-elle évolutive pour des problèmes complexes du monde réel ? comme suit.

Dans cet article, nous utilisons principalement deux méthodes pour étudier les sous-problèmes ci-dessus. Premièrement, pour les trois premiers sous-problèmes, des études de cas complexes, réelles et spécifiques à un domaine sont utilisées pour examiner les performances et l'évolutivité de plusieurs méthodes PIML différentes. Pour chaque sous-problème, nous présentons une étude de cas, proposons une technique PIML (ou diverses techniques PIML) pour le résoudre et évaluons comment la technique peut être étendue à ce contexte. Deuxièmement, pour le dernier sous-problème, nous nous concentrons sur une seule technologie PIML à usage général et évaluons et améliorons son évolutivité. Les trois premiers sous-problèmes sont étudiés dans des chapitres séparés de cette thèse (chapitres 3 à 5 respectivement), et leurs études de cas proviennent toutes des domaines de la science lunaire et de la géophysique. Le dernier sous-problème sera étudié au chapitre 6. Enfin, nous discutons et résumons les implications de chaque chapitre pour nos principales questions de recherche au chapitre 7.

Généalogie méthode SciML. Ce graphique montre à quel point les différents types de méthodes SciML présentés dans ce chapitre sont « puissants » pour la connaissance scientifique. Notez que la force d'une contrainte scientifique est un concept plutôt vague ; dans ce diagramme, nous la définissons comme la proximité d'une approche SciML avec un flux de travail traditionnel. Les approches intermédiaires combinent également le ML avec certains aspects des flux de travail traditionnels, comme les méthodes de boucle qui entrelacent les solveurs itératifs traditionnels avec les modèles ML. De plus, notre mission est quelque peu subjective, ce chiffre sert donc simplement à exprimer la tendance générale.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!