Le « Sparse coding » passe de la théorie à la pratique ! Nouveaux travaux du professeur Ma Yi dans NeurIPS 2022 : les performances et la robustesse de la convolution clairsemée dépassent ResNet

Bien que les réseaux de neurones profonds aient de fortes performances empiriques en matière de classification d'images, ces modèles sont souvent considérés comme des « boîtes noires » et sont surtout critiqués pour être « difficiles à expliquer ».

En revanche, les modèles convolutionnels clairsemés sont également des outils puissants pour analyser des images naturelles, qui supposent qu'un signal peut être composé d'une combinaison linéaire de plusieurs éléments dans le dictionnaire convolutionnel, pour s'exprimer, il a une bonne théorique. l'interprétabilité et la plausibilité biologique.

Mais dans les applications pratiques, bien que le modèle de convolution clairsemée fonctionne en principe, il ne montre pas les avantages en termes de performances qu'il mérite par rapport aux réseaux profonds conçus empiriquement.

Récemment, le groupe de recherche du professeur Ma Yi a publié un nouvel article à NeurIPS 2022, examinant l'application des modèles de convolution clairsemés dans la classification d'images, et a résolu avec succès les performances empiriques et la fiabilité des modèles de convolution clairsemés.

Lien papier : https://arxiv.org/pdf/2210.12945.pdf​

Lien code : https://github.com/Delay-Xili/SDNet​

La couche d'optimisation différenciable proposée dans l'article utilise le Convolutional Sparse Coding (CSC) pour remplacer la couche quasi-convolutionnelle standard.

Les résultats montrent que par rapport aux réseaux de neurones traditionnels, ces modèles ont des performances empiriques tout aussi solides sur les ensembles de données CIFAR-10, CIFAR-100 et ImageNet.

En exploitant les propriétés de récupération robustes de la modélisation clairsemée, les chercheurs montrent en outre qu'avec seulement un simple compromis approprié entre les termes de régularisation clairsemés et les termes de reconstruction des données, ces modèles peuvent survivre à la corruption d'entrée ainsi que Les perturbations contradictoires sont plus robustes .

Le professeur Ma Yi a obtenu un double baccalauréat en automatisation et mathématiques appliquées de l'Université Tsinghua en 1995, puis a étudié à l'Université de Californie, Berkeley, États-Unis, et a obtenu une maîtrise en EECS en 1997, un une maîtrise en mathématiques et un doctorat en EECS en 2000 Bachelor of Science.

Après avoir obtenu son diplôme, il a enseigné à l'Université de l'Illinois à Urbana-Champaign et est devenu le plus jeune professeur agrégé de l'histoire du Département de génie électrique et informatique.

En 2009, il a occupé le poste de chercheur principal au sein du Visual Computing Group de Microsoft Research Asia. En 2014, il rejoint à temps plein l’École des sciences et technologies de l’information de l’Université ShanghaiTech.

A rejoint l'Université de Californie à Berkeley et le Tsinghua-Berkeley Shenzhen Institute en 2018. Il est actuellement professeur au Département de génie électrique et d'informatique de l'Université de Californie à Berkeley. Il est également membre de l'IEEE, ACM. Fellow et SIAM Fellow

Recherches du professeur Ma Yi Ses intérêts incluent la vision par ordinateur 3D, les modèles de faible dimension pour les données de haute dimension, l'optimisation de l'évolutivité et l'apprentissage automatique. Les sujets de recherche récents incluent la reconstruction et l'interaction géométriques 3D à grande échelle. et la relation entre les modèles de faible dimension et les réseaux profonds.

Bien que les réseaux convolutifs profonds (ConvNets) soient devenus la méthode courante de classification d'images et que leurs performances dépassent les autres modèles, ses composants internes tels que la convolution, les fonctions non linéaires et la normalisation, etc. les données n’ont pas encore été expliquées.

Bien que la modélisation de données clairsemées, soutenue par la capacité d'apprendre des représentations interprétables et de solides garanties théoriques (telles que la gestion des données corrompues), ait été largement utilisée dans de nombreuses applications de traitement du signal et de l'image, ses performances dans des données telles que ImageNet The les performances de classification sur l’ensemble sont encore inférieures aux modèles empiriques profonds.

Même les modèles clairsemés avec de fortes performances ont encore des défauts :

1) La structure du réseau doit être spécialement conçue, ce qui limite l'applicabilité du modèle

2) La vitesse de calcul de la formation est de plusieurs ordres de grandeur ; ampleur plus lente ;

3) Il ne présente pas d'avantages évidents en termes d'interprétabilité et de robustesse.

Les chercheurs ont proposé un cadre de reconnaissance visuelle dans cet article, démontrant que la modélisation clairsemée peut être combinée avec l'apprentissage profond grâce à une conception simple, en supposant que l'entrée de la couche peut être composée de quelques atomes dans un dictionnaire partagé par tous les points de données. (atomes), obtenant ainsi les mêmes performances que les ConvNets standards tout en ayant une meilleure interprétabilité et stabilité hiérarchique.

Cette méthode encapsule la modélisation clairsemée dans une couche implicite et l'utilise en remplacement de la couche convolutive dans les ConvNets standard.

Par rapport à la fonction explicite utilisée dans la couche classique entièrement connectée ou convolutive, la couche cachée utilise une fonction implicite. La couche cachée dans cet article est définie sur la base du problème d'optimisation des paramètres d'entrée et de poids de la couche, et la sortie de la couche cachée est la solution au problème d'optimisation.

Étant donné un signal d'entrée multidimensionnel, la fonction de la couche peut être définie pour effectuer un mappage inverse vers une meilleure sortie clairsemée. Le nombre de canaux de sortie peut être différent de l'entrée, trouvant ainsi un optimal pour le Lasso ci-dessus. problème d'optimisation de type solution clairsemée.

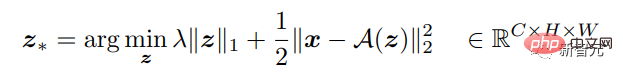
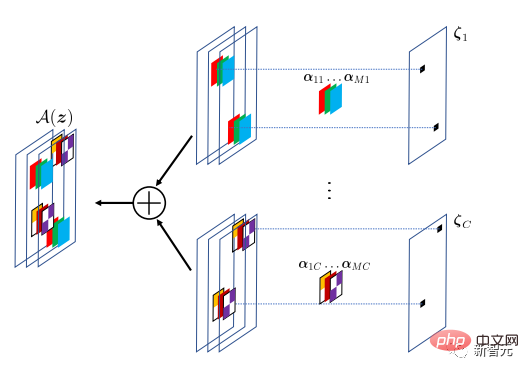
Cette couche cachée implémente le modèle Convolutional Sparse Coding (CSC), où le signal d'entrée est approximé par une combinaison linéaire clairsemée d'atomes dans un dictionnaire convolutif. Ce dictionnaire convolutif peut être considéré comme les paramètres de la couche CSC, qui est entraînée par rétro-propagation.

L'objectif du modèle CSC est de reconstruire le signal d'entrée via l'opérateur A(z), où la carte des caractéristiques z spécifie la position et la valeur du filtre de convolution dans A. Pour être tolérante aux différences de modélisation, la reconstruction n’a pas besoin d’être exacte.

Sur la base du mappage entrée-sortie déterminé de la couche CSC, la propagation vers l'avant peut être effectuée en résolvant l'optimisation appropriée, et la propagation vers l'arrière peut être effectuée en obtenant le gradient de la solution de coefficient optimale par rapport à l'entrée x et au paramètre. UN .

Ensuite, l'ensemble du réseau avec la couche CSC peut être formé à partir des données étiquetées de bout en bout en minimisant la perte d'entropie croisée.

Résultats expérimentaux

Comparaison des performances de classification​

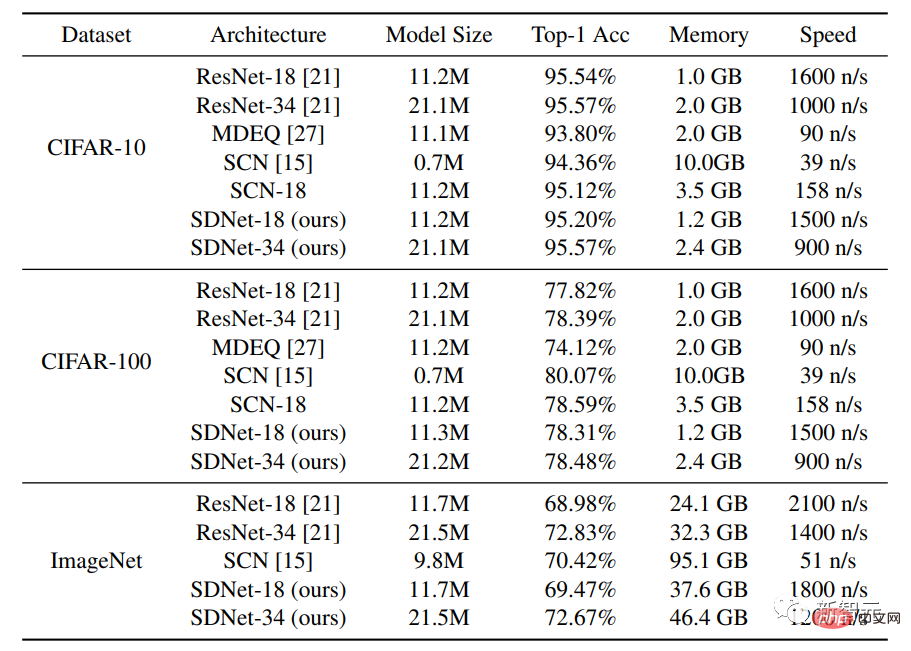
Les ensembles de données utilisés dans l'expérience sont CIFAR-10 et CIFAR-100, chaque ensemble de données contient 50 000 images d'entraînement et 10 000 images de test, chaque image a une taille de 32 × 32 et des canaux RVB.

En plus de comparer la méthode avec les architectures de réseau standard ResNet-18 et ResNet-34, les chercheurs ont également comparé le modèle MDEQ avec une architecture de couches cachées et le SCN avec une architecture de modélisation clairsemée.

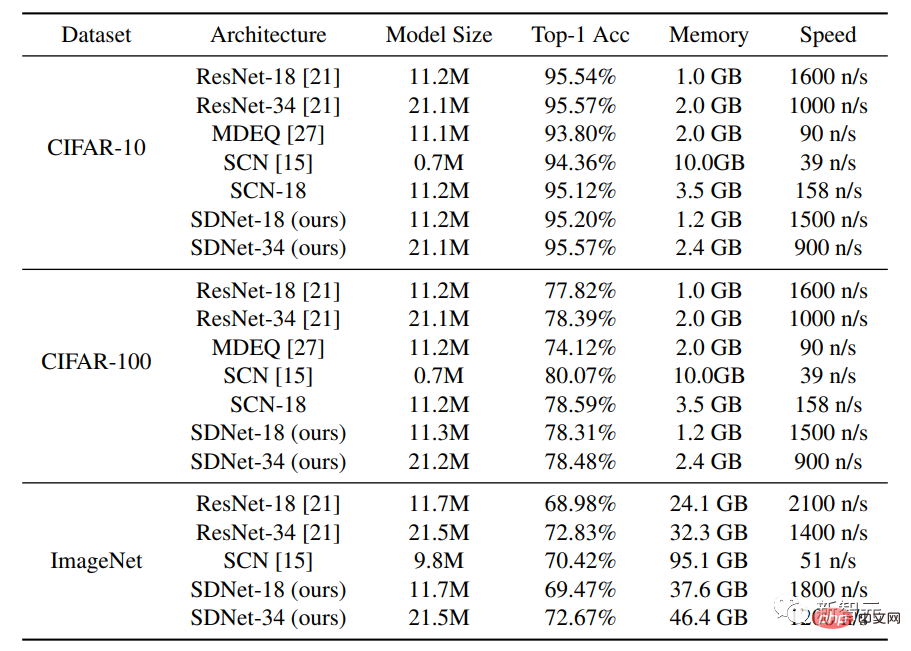
Les résultats expérimentaux montrent que sous une échelle de modèle similaire, la précision Top-1 du SDNet-18/34 est similaire ou supérieure à celle de ResNet-18/34, tout en ayant une vitesse d'inférence similaire. Les résultats démontrent le potentiel de ce réseau en tant qu'alternative puissante aux modèles basés sur les données existants, car les modèles SDNet présentent des avantages supplémentaires dans la gestion des images endommagées.

Après avoir comparé le modèle SDNet-18 avec le modèle MDEQ de taille similaire, on constate que le SDNet-18 est non seulement plus précis que le MDEQ, mais aussi beaucoup plus rapide (>7 fois). Il est à noter que le MDEQ ne peut pas gérer les données endommagées comme le SDNet.

Le réseau SCN, qui utilise également une modélisation clairsemée, a atteint une précision Top-1, mais un inconvénient important de SCN est que sa vitesse de formation est très lente. La raison peut être que SCN utilise un modèle de codage clairsemé basé sur des correctifs. pour les images. Par rapport au modèle de codage convolutionnel clairsemé, il doit résoudre des problèmes de codage plus clairsemés à chaque passage direct et ne peut pas bénéficier du calcul parallèle.

Gestion d'inférence robuste des perturbations d'entrée

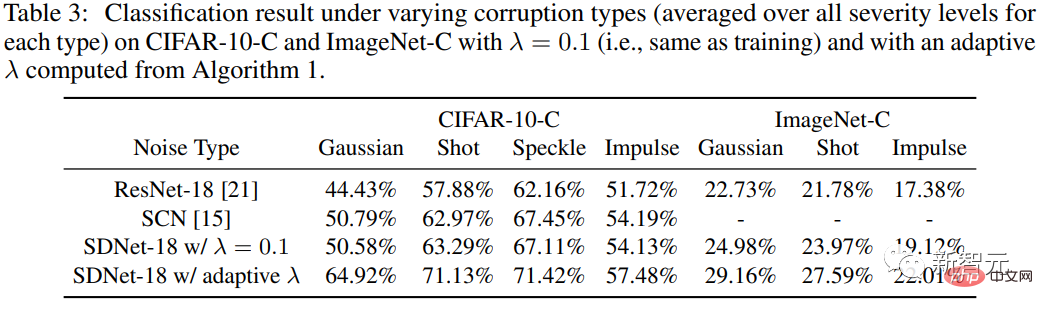
Pour tester la robustesse de la méthode aux perturbations d'entrée, les chercheurs ont utilisé l'ensemble de données CIFAR-10-C, dans lequel les données ont été affectées par différents types de bruit synthétique et gravement endommagé.

Étant donné que la couche CSC du modèle pénalise la différence d'entrée entre le signal d'entrée et le signal reconstruit, SDNet devrait théoriquement être plus adapté au traitement du bruit additif.

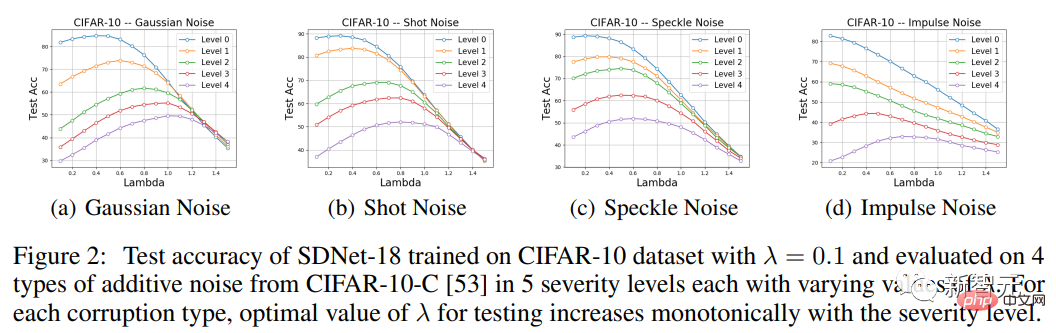
La partie expérimentale se concentre donc principalement sur les quatre types de bruit additif dans CIFAR-10-C, à savoir le bruit gaussien, le bruit de grenaille, le bruit speckle et le bruit impulsionnel, puis évalue la précision du SDNet-18, et ses performances sont comparées à celles de ResNet-18.

On peut constater que pour différents types de bruit et différentes sévérités (à l'exception des bruits impulsifs de niveaux 0, 1 et 2), le choix approprié d'une valeur λ différente de celle utilisée lors de l'entraînement peut contribuer à améliorer les performances du test.

En particulier, la courbe de précision en fonction de λ présente une forme unimodale, avec des performances d'abord croissantes puis décroissantes. De plus, dans chaque type de corruption de données, la valeur λ à laquelle les pics de performances sont atteints augmente de façon monotone avec la gravité de la corruption, une observation conforme aux attentes.

Gestion des perturbations contradictoires

Les chercheurs ont utilisé PGD pour générer des perturbations contradictoires pour SDNet (λ=0,1) sur l'ensemble de données de test CIFAR-10. Le paradigme L∞ de la perturbation est 8/255, et la forme normale de la perturbation L2 est de 0,5.

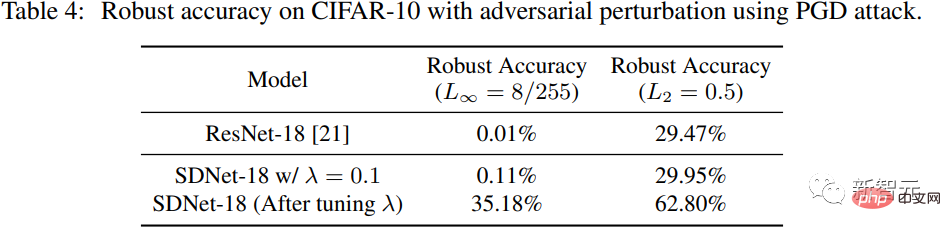
Par rapport à ResNet-18, nous pouvons voir que dans le cas de λ=0,1, les performances de SDNet ne sont pas bien meilleures que celles de ResNet, mais la précision de la robustesse peut être grandement améliorée en ajustant le paramètre λ .

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!