
Les nombres à virgule flottante sont composés de trois parties : le symbole, le code d'exposant et la mantisse. Les nombres à virgule flottante sont divisés en nombres à virgule flottante simple précision et en nombres à virgule flottante double précision. nombres est -3.4E38 ~ 3.4E38, la plage des nombres à virgule flottante double précision est -1.79E+308 ~ +1.79E+308
[Recommandé cours : Tutoriel JavaScript】
Représentation d'un nombre à virgule flottante
Un nombre à virgule flottante (Floating Point Number) se compose de trois composants de base : Signe (Signe), Développer le code ( Exposant) et mantisse (Mantisse). Les nombres à virgule flottante peuvent généralement être représentés dans le format suivant :
| S | P | M |
où S est le bit de signe, P est le code de l'exposant et M est la mantisse.
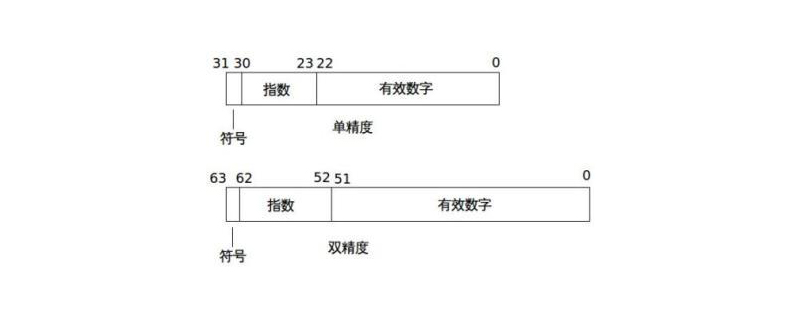
Selon la définition de la norme IEEE (Institute of Electrical and Electronics Engineers) 754, les nombres à virgule flottante simple précision sont de 32 bits (soit 4 octets), et les nombres à virgule flottante double précision sont 64 bits (soit 8 octets) de. Le nombre de chiffres occupés par S, P et M et la méthode de représentation des deux sont indiqués dans le tableau suivant :
|
S | P | M td> | Représenter la formule | Offset | ||||||||||||||||||
| 1 (31ème position) | 8 (chiffres 30 à 23) | 23 (chiffres 22 à 0) | (-1)^S*2(P-127)*1.M | 127 | |||||||||||||||||||
| Nombre à virgule flottante double précision | 1 (63ème position) | 11 (62 à 52 bits) | 52 (51 à 0 bits) | (-1)^S*2(P -1023)* 1.M | 1023 |
où S est le bit de signe, seulement 0 et 1, indiquant respectivement positif et négatif
P est le code exposant, généralement représenté par le code de trame (le code de trame et le code complémentaire n'ont que le bit de signe opposé, le reste est le même. Pour les nombres positifs, le code original, le complément et le complément sont les mêmes ; pour les nombres négatifs, le complément est l'inversion de tous les codes originaux de leurs valeurs absolues, puis l'ajout de 1). Le code d'exposant peut être un nombre positif ou un nombre négatif. Afin de gérer le cas d'un exposant négatif, la valeur réelle de l'exposant doit être ajoutée avec une valeur de biais (Bias) comme valeur stockée dans le champ de l'exposant. du nombre simple précision est 127, la valeur d'écart du double est 1023. Par exemple, la valeur réelle de l'exposant 0 de simple précision sera stockée sous la forme 127 dans le champ de l'exposant, tandis que 64 stockée dans le champ de l'exposant représente la valeur réelle de l'exposant -63. L'introduction du biais permet aux nombres à simple précision de. exprimer en fait la valeur de l'exposant. La plage devient -127 à 128 (les deux extrémités incluses).
M est la mantisse, où les nombres en simple précision ont une longueur de 23 bits et les nombres en double précision ont une longueur de 52 bits. La norme IEEE exige que les nombres à virgule flottante soient canoniques. Cela signifie que le côté gauche du point décimal de la mantisse doit être 1, donc lors de la sauvegarde de la mantisse, le 1 devant le point décimal peut être omis, libérant ainsi un bit binaire pour enregistrer plus de mantisses. Cela exprime en fait la mantisse de 24 bits avec un champ de mantisse de 23 bits de long. Par exemple, pour les nombres simple précision, le binaire 1001,101 (correspondant à la décimale 9,625) peut être exprimé sous la forme 1,001101 × 23, donc la valeur réellement stockée dans le champ de mantisse est 0011010000000000000000000, c'est-à-dire que le 1 à gauche du point décimal est supprimé et 0 est utilisé à droite.
Selon les exigences standard, les valeurs qui ne peuvent pas être enregistrées avec précision doivent être arrondies à la valeur enregistrable la plus proche, c'est-à-dire que si elle est inférieure à la moitié, elle sera arrondie, et si elle est supérieure à la moitié (y compris la moitié ), il sera arrondi. Cependant, pour les nombres binaires à virgule flottante, il existe une règle supplémentaire, à savoir que lorsque la valeur à arrondir est exactement la moitié, elle n'est pas simplement arrondie, mais la dernière des deux valeurs stockables qui sont également espacées. avant et après est pris. Le nombre de chiffres significatifs est zéro.
Selon l'analyse ci-dessus, la norme IEEE 754 définit la plage de représentation des nombres à virgule flottante comme :
| Binaire | Décimal | |||||||||
| Nombre à virgule flottante simple précision | ± (2-2^-23) × 2127 | ~ ± 10^38.53 | |||||||||
| ± (2-2^-52) × 21023 | ~ ± 10^308.25 |
La représentation des nombres à virgule flottante a une certaine plage. Lorsqu'elle dépasse la plage, un débordement (Flow) se produit. De manière générale, les données supérieures à la valeur absolue maximale sont appelées débordement (Overflow), et les données inférieures à la valeur absolue maximale. la valeur absolue minimale est appelée sous-débit (Underflow).
Conventions de représentation pour les nombres à virgule flottante
Les nombres à virgule flottante simple précision et les nombres à virgule flottante double précision sont tous deux définis par la norme IEEE 754 , et il existe des conventions spéciales. Par exemple :
1. Lorsque P=0 et M=0, cela signifie 0.
2. Lorsque P=255 et M=0, cela signifie l'infini, et le bit de signe est utilisé pour déterminer s'il est infini positif ou infini négatif.
3. Lorsque P=255 et M≠0, cela signifie NaN (Pas un nombre, pas un nombre).
Nombres à virgule flottante non standard
Lorsque deux nombres à virgule flottante avec des valeurs absolues extrêmement petites sont soustraits, l'exposant de la différence peut dépasser la plage autorisée, et ne peut être qu'environ 0 à la fin. Afin de résoudre de tels problèmes, la norme IEEE a introduit les nombres à virgule flottante dénormalisés, qui stipule que lorsque l'exposant d'un nombre à virgule flottante est la valeur minimale autorisée de l'exposant, la mantisse n'a pas besoin d'être normalisée. Avec les nombres à virgule flottante non standard, la restriction implicite du bit de mantisse est supprimée et les nombres à virgule flottante avec des valeurs absolues plus petites peuvent être stockés. De plus, comme il n'est plus limité par le champ de mantisse implicite, le problème mentionné ci-dessus concernant les différences extrêmement petites n'existe pas, car toutes les différences entre les nombres à virgule flottante qui peuvent être enregistrées peuvent également être enregistrées.
Selon la définition de la norme IEEE 754, la plage de représentation des nombres à virgule flottante canoniques et non canoniques peut être résumée comme le tableau suivant :
|
Nombres à virgule flottante normaux | Nombre à virgule flottante non standard | Plage décimale approximative | ||||||||||||
| Nombre à virgule flottante simple précision | ± 2^-149 à (1-2^-23)*2^-126 | ± 2^-126 à (2-2^-23)*2^127 | ± ~10^-44,85 à ~10^38,53 | ||||||||||||
| Point flottant double précision number | ± 2^-1074 à (1-2^- 52)*2^-1022 | ± 2^-1022 à (2-2^-52)*2^1023 td> | ± ~10^-323.3 à ~10^308.3 |
Normes liées à l'IEEE 754
La conclusion de ce L'article est basé sur la norme IEEE 754. Une autre norme est IEEE 854. Cette norme concerne les nombres décimaux à virgule flottante, mais elle ne spécifie pas de format spécifique, elle est donc rarement utilisée. De plus, à partir de 2000, la norme IEEE 754 a commencé à être révisée, connue sous le nom d'IEEE 754R, dans le but d'intégrer les normes IEEE 754 et IEEE 854. Les révisions du format à virgule flottante de cette norme incluent : 1. L'ajout des formats à virgule flottante binaire 16 bits et 128 bits ; 2. L'ajout du format à virgule flottante décimal et l'adoption du format proposé par IBM ;
Résumé : ce qui précède représente l'intégralité du contenu de cet article, j'espère qu'il sera utile à tout le monde.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!