Cette fois, je vais vous apporter une explication détaillée d'un exemple d'algorithme de tri dans le front-end. Quelles sont les précautions lors de l'utilisation de l'algorithme de tri dans le front-end. cas pratique, jetons un coup d'oeil.
Avant-hier, j'ai vu un article sur Zhihu se plaignant de l'algorithme de tri rapide du professeur Ruan Yifeng. Je voudrais ajouter ici une digression. Je pense que personne ne peut faire d'erreurs. être un sage. Je le crois. Les livres sont pires que pas de livres. Le processus d'apprentissage est le processus de découverte et de correction constante d'erreurs. Nous devrions être heureux lorsque quelqu'un nous aide à corriger cette erreur, mais je ne pense pas que nous devrions critiquer. Professeur Ruan Yifeng. Il apprend et corrige également constamment les erreurs, donc tout le monde est pareil, il n'y a pas lieu de tromper. Et si ce n'était pas lui qui avait commis l'erreur, mais une personne plus puissante ? JavaScript ? Donc tout le monde fera des erreurs, et nous devrions également réfléchir davantage et être sceptiques et toujours nous demander si c'est la solution optimale et s'il existe une meilleure solution.
Et moi, en tant que professionnel du front-end en informatique, je n'arrive pas à bien mettre en œuvre diverses tâches. J'ai eu très honte de l'algorithme de tri basé sur cette idée, j'ai donc pris le temps de lire attentivement le livre "Données". Analyse de la structure et des algorithmes : Langage CDescription + Version chinoise.pdf>> Ci-dessous, je résumerai les algorithmes de tri de diverses idées que je comprends. J'espère que cela pourra vous donner des références et des gains s'il y en a. si quelque chose ne va pas, veuillez le signaler. Vous pouvez également partager ce que vous pensez être une meilleure idée. Je pense que tout le monde peut travailler ensemble. Le plus heureux est d'apprendre et de progresser ensemble ~
(1) Le concept de complexité temporelle
Algorithme La complexité temporelle de est une fonction qui décrit qualitativement le temps d'exécution d'un algorithme. est couramment utilisé, à l'exclusion des termes d'ordre inférieur et des coefficients des termes d'ordre élevé de cette fonction
(2) Méthode de calcul
Généralement, le nombre d'exécutions d'opérations de base dans. un algorithme est fonction de la taille du problème n, représentée par T(n). S'il existe une certaine fonction auxiliaire f(n), telle que lorsque n s'approche de l'infini, la valeur limite de T(n)/f(n ) est une constante non nulle, alors f(n) est une fonction du même ordre de grandeur que T(n), notée T(n) = O(f (n)), appelez O(f(n) ) la complexité temporelle asymptotique de l'algorithme, appelée complexité temporelle
Analyse : À mesure que le module n augmente à tout moment, le taux de croissance du temps d'exécution de l'algorithme est proportionnel à la croissance. taux de f(n), donc plus f(n) est petit, plus la complexité temporelle de l'algorithme est faible et plus l'efficacité de l'algorithme est élevée.
Lors du calcul de la complexité temporelle, découvrez d'abord les opérations de base de l'algorithme, puis calculez le nombre d'exécutions des opérations de base, et trouvez f(n) du même ordre de grandeur que T(n) (son même ordre de grandeur a généralement le suivant : 1 , log₂n , n, nlog₂n, n au carré, n au cube), si T(n) / f(n) trouve la limite pour obtenir une constante c, alors la complexité temporelle T(n) = O(f(n)) :
Par exemple :
for(i = 1; i<p style="text-align: left;">Nous pouvons obtenir T(n) = n^3 + n^2, et nous pouvons déterminer que n^3 est T (n) sont du même ordre de grandeur, f(n)=n^3 ; alors T(n) / f(n) = 1 + 1/n La limite est constante 1, donc la complexité temporelle de cet algorithme. est : <br> T(n ) = O(n^3);</p><p style="text-align: left;"><strong>Remarque : Pour plus de commodité, j'utiliserai N pour représenter le nombre d'éléments du tableau.</strong></p><h1 style="text-align: left;">2. Algorithme de tri</h1><h2 style="text-align: left;">2.1 <a href="//m.sbmmt.com/code/12106.html" target="_blank">Tri à bulles</a>
</h2><h3 style="text-align: left;">2.1.1 Idée principale :</h3><p style="text-align: left;">L'idée principale du tri à bulles est d'effectuer un tableau de longueur n Traversal, i passe de n-1 à 1, et la valeur maximale des i premiers éléments du tableau est placée à la position i. Supposons que le tri à bulles soit une colonne d'eau verticale. est que les grandes valeurs (les plus lourdes) continuent de couler, les petites valeurs (les plus légères) continuent de flotter, de sorte qu'une fois le parcours terminé, la valeur à chaque position est plus grande que sa valeur précédente, et le tri est terminé.</p><h3 style="text-align: left;">2.1.2 Complexité temporelle</h3><p style="text-align: left;">Complexité temporelle dans le pire des cas : o(n^2);<br>Complexité temporelle dans le meilleur des cas : o(n^2) ;</p><h3 style="text-align: left;">2.1.3 Processus de tri Illustration : </h3><p style="text-align: left;"><strong>La boucle de sortie dans l'illustration consiste à sortir de la boucle intérieure </strong><br><img src="https://img.php.cn/upload/article/000/061/021/975255cd4031086ad718d4dc21df07d0-0.png" alt="Explication détaillée des exemples dalgorithmes de tri dans le front-end" title="Explication détaillée des exemples dalgorithmes de tri dans le front-end"></p><h3 style="max-width:90%">2.1.4 代码实现:</h3><h4 style="text-align: left;">冒泡排序-非递归实现</h4><pre class="brush:php;toolbar:false">function bubbleSort(arr) {
for(var i = arr.length - 1; i > 1; i--) {
for(var j=0; j arr[j+1]) {
var temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
return arr;
}
var arr = [34,8,64,51,32,21];
bubbleSort(arr); // [8, 21, 32, 34, 51, 64]function bubbleSort(arr, n) {
if(n arr[j+1]) {
var temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
return bubbleSort(arr, --n);
}
}
var arr = [34,8,64,51,32,21];
bubbleSort(arr, arr.length); // [8, 21, 32, 34, 51, 64]插入排序有 n-1 趟排序组成,对于 i=1 到 i=n-1 趟,内层循环j从 i 到 1, 如果这其中有 j-1 位置上的元素大于 i 位置上的元素,就将该元素后移,知道条件不成立退出循环,这个时候大的值都被移动到后面了,j这个位置就是i位置上的元素应该在的位置.这样保证了每次循环i位置前的所有元素都是排好序的,新的循环就只需要 将 i 位置上的元素 和 j-1(也就是初始的 i-1) 位置上的元素作比较,如果大于则无需再往前比较,如果小于则继续往前比较后移.
最坏情况下的时间复杂度: o(n^2);
最好情况下的时间复杂度: o(n);
图解中的出循环是退出内层循环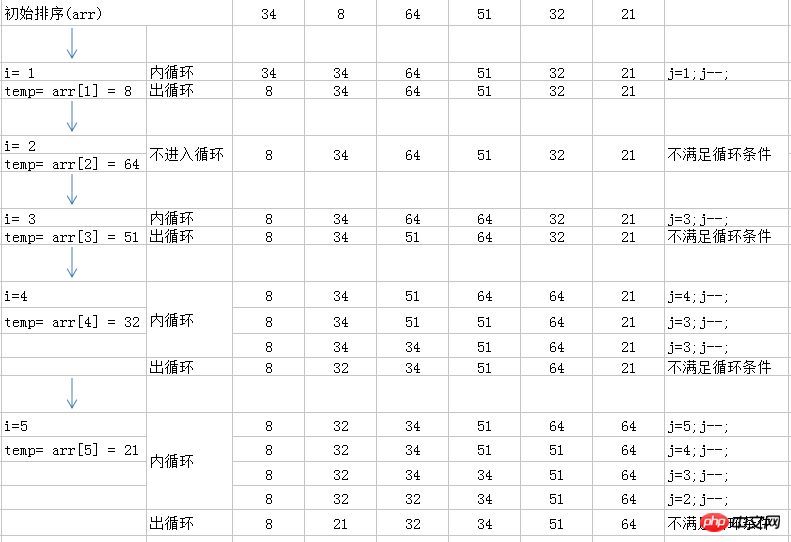
function insertSort(arr) {
var n = arr.length,temp = 0;
for(var i = 1; i 0 && arr[j-1] > temp; j--) {
arr[j] = arr[j - 1];
}
arr[j] = temp;
}
return arr;
}
var arr = [34,8,64,51,32,21];
insertSort(arr); // [8, 21, 32, 34, 51, 64]function insertSort(arr, n) {
if(n > 0 && n 0 && arr[j - 1] > temp) {
arr[j] = arr[j - 1];
j--;
}
arr[j] = temp;
i++;
return insertSort(arr, i);
}
return arr;
}
var arr = [34,8,64,51,32,21];
insertSort(arr, 1); // [8, 21, 32, 34, 51, 64]; // 这个函数的调用限定了第一次调用n的值只能传1顾名思义,快速排序是在实践中最快的已知排序算法,它的平均运行时间是O(Nlog₂N).快速排序的关键在于枢纽元的选取,有一种比较推荐的选取方法就是选取左端的值,右端的值,中间位置的值(L(left + right) / 2)这三个数的中位数.举例: 输入为8,1,4,9,6,3,5,2,7,0, 左边元素8, 右边元素0,中间位置上的元素L(0+9)/2是4位置上的元素是6,L在表示向下取整.
8,0,6的中位数,先排序0,6,8, 这三个数的中位数是6.
通过一趟排序将要排序的部分分割成独立的两部分,其中一部分数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据进行快速排序,整个排序过程可以递归进行,依次达到整个数据变成有序序列.
第一步: 设置两个变量i,j,排序开始的时候: i=left,j=right-1,left和right分别表示要进行快速排序序列的起始索引和结束索引;
第二步: 从数组中随机选取一个元素,将其与arr[left]进行交换,即privot = arr[left],保证每一次的基准值都在序列的最左边;
第三步: 由j开始向前搜索,即由后开始向前搜索(j--),找到第一个小于privot 的值arr[j],将arr[i]与arr[j]互换;
第四步: 从i开始向后搜索,即由前开始向后搜索(i++),找到一个大于privot 的arr[i],将arr[i]与arr[j]互换;
第五步: 重复第三步和第四步,直到不满足i
平均情况下的时间复杂度: o(nlog₂n);
最好情况下的时间复杂度: o(n);
function quickSort(arr, left, right) {
if(left >= right) return;
var i = left;
var j = right - 1;
var privot = arr[left];
//console.log(privot);
while(i = privot) j--;
arr[i] = arr[j];
while(i<j var quicksort><h4 style="text-align: left;">快速排序-非递归实现</h4>
<pre class="brush:php;toolbar:false">function mainProduce(arr, left, right) {
var i = left, j = right - 1;
var rendomIndex = Math.floor(Math.random() * (j - i)) + left;
var temp = arr[left];arr[left] = arr[rendomIndex];arr[rendomIndex] = temp;
var privot = arr[left];
while(i = privot) j--;
var temp = arr[i];arr[i] = arr[j];arr[j] = temp;
while(i<j> left + 1) {
s.push(left);s.push(mid);
}
if(mid left + 1) {
s.push(left);s.push(mid);
}
if(mid <h2 style="text-align: left;">2.4 希尔排序</h2>
<h3 style="text-align: left;">2.4.1 主要思想</h3>
<p style="text-align: left;">希尔排序是把记录按照下标的一定增量分组,对每组使用插入排序;随着增量逐渐减少,分割的数组越来越大,当增量减至1,整个<a href="//m.sbmmt.com/code/54.html" target="_blank">数组排序</a>完成,算法终止.</p>
<h3 style="text-align: left;">2.4.2主要步骤</h3>
<p style="text-align: left;">第一步: 选取一个增量d,初始值是Math.floor(len/2);<br>第二步: 然后将数组中间隔为增量d的组成新的分组,然后对这个分组的元素排序,完成排序后,增量除以2得到新的增量;<br>第三步: 重复第二步,直到增量为1,间隔为1的元素组成的分组就是整个数组,然后再对整个数组进行插入排序,得到最后排序后数组.</p>
<p style="text-align: left;">希尔排序是不稳定的,它在不断地交换的过程中会改变原来相等的元素的顺序.</p>
<h3 style="text-align: left;">2.4.3 时间复杂度</h3>
<p style="text-align: left;">平均情况下的时间复杂度: o(nlog₂n);<br>最好情况下的时间复杂度: o(n);</p>
<h3 style="text-align: left;">2.4.4 Explication détaillée des exemples dalgorithmes de tri dans le front-end</h3>
<p style="text-align: left;"><img src="https://img.php.cn/upload/article/000/061/021/2f13ca0ab50333d1dad5851595e7225d-3.jpg" alt="Explication détaillée des exemples dalgorithmes de tri dans le front-end" title="Explication détaillée des exemples dalgorithmes de tri dans le front-end"></p>
<p style="text-align: left;">图片源于自百度百科: 图片来源</p>
<h3 style="text-align: left;">2.4.5 代码实现:</h3>
<h4 style="text-align: left;">希尔排序-递归实现</h4>
<pre class="brush:php;toolbar:false">function shellSort(arr, increment) {
var len = arr.length;
if(increment > 0) {
for(var i = increment; i = 0 && arr[j] > arr[j + increment]; j -= increment) {
var temp = arr[j];
arr[j] = arr[j + increment];
arr[j + increment] = temp;
}
}
return shellSort(arr, Math.floor(increment/2));
}
return arr;
}
var arr = [49,38,65,97,76,13,27,49,55,04];
shellSort(arr, Math.floor(arr.length / 2));function shellSort(arr) {
var len = arr.length;
for(var increment = Math.floor(len / 2); increment > 0; increment = Math.floor(increment / 2)) {
for(var i = increment; i = 0 && arr[j] > arr[j + increment]; j -= increment) {
var temp = arr[j];
arr[j] = arr[j + increment];
arr[j + increment] = temp;
}
}
}
return arr;
}
var arr = [49,38,65,97,76,13,27,49,55,04];
shellSort(arr);第一步: 将一个数组以中间值截取为为两个数组,分别将其排好序;
第二步: 申请一个空间,使其大小为两个已经排序的序列之和,该空间用来存放合并后的序列;
第三步: 设定两个指针,分别指向两个已排序序列的起始位置;
第四步: 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置.
重复第四步直到有一个某一指针超出序列尾;
将另一序列的所有元素复制到合并序列尾.
归并排序是稳定的,它在不会改变原来相等的元素的顺序.
平均情况下的时间复杂度: O(nlog₂n);
最好情况下的时间复杂度: O(nlog₂n) ;
var result = [];
function mergeArray(left, right) {
result = [];
while(left.length > 0 && right.length > 0) {
if(left[0] <p>相信看了本文案例你已经掌握了方法，更多精彩请关注php中文网其它相关文章！</p><p>推荐阅读：</p><p><a href="//m.sbmmt.com/js-tutorial-398003.html" target="_blank">React结合TypeScript和Mobx步骤详解</a><br></p><p><a href="//m.sbmmt.com/js-tutorial-398045.html" target="_blank">react实现选中li高亮步骤详解</a><br></p>Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Algorithme de remplacement de page
NumberFormatException
oicq
Quelles sont les méthodes pour changer instantanément l'IP dans les vps dynamiques ?
Qu'est-ce que la HD sur téléphone portable ?
Méthodes de réparation des vulnérabilités des bases de données
Quelle est la balise article utilisée pour définir ?
quelle est l'adresse mac
![[Web front-end] Démarrage rapide de Node.js](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
