
Le programme de tri par fusion en Java est l'un des algorithmes les plus utilisés et les plus efficaces. Le tri par fusion est basé sur la technique diviser pour régner qui consiste à diviser un problème donné en plusieurs sous-problèmes et à résoudre chaque sous-problème indépendamment. Lorsque les sous-problèmes sont résolus, nous combinons leurs résultats pour obtenir la solution finale au problème. L'algorithme de tri par fusion peut être implémenté en utilisant la récursion car il implique de travailler avec des sous-problèmes plutôt qu'avec le problème principal.
Considérons un tableau non trié qui doit être trié à l'aide de l'algorithme de tri par fusion. Voici les étapes à suivre pour trier un tableau avec des valeurs : 18, 8, 4, 13, 10, 12, 7 et 11 :
Commencez votre cours de développement de logiciels libres
Développement Web, langages de programmation, tests de logiciels et autres
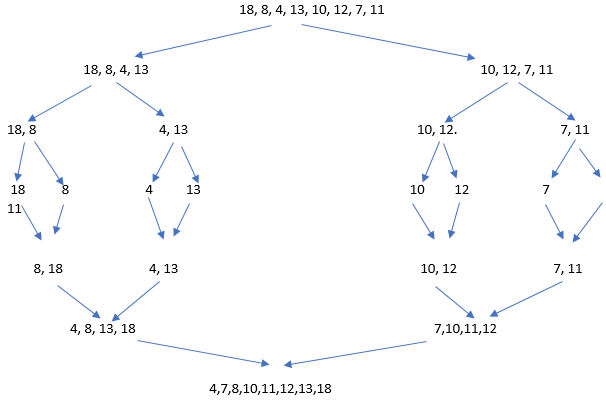
Voici un exemple de code montrant l'implémentation du tri par fusion en Java :
Code :
package com.edubca.sorting;
public class MergeSort {
private int[] array;
private int[] tempMergedArr;
private int length;
public static void main(String a[]){
int[] inputArr = {18, 8, 4, 13, 10, 12, 7, 11};
MergeSort mergeSort = new MergeSort();
mergeSort.sort(inputArr);
for(int i:inputArr){
System.out.print(i + " ");
}
}
public void sort(int inputArr[]) {
this.array = inputArr;
this.length = inputArr.length;
this.tempMergedArr = new int[length];
performMergeSort(0, length - 1);
}
private void performMergeSort(int lowerIndex, int higherIndex) {
if (lowerIndex < higherIndex) {
int middle = lowerIndex + (higherIndex - lowerIndex) / 2;
// Sort the left side of the array call performMergeSort recursively
performMergeSort(lowerIndex, middle);
// Sort the right side of the array call performMergeSort recursively
performMergeSort(middle + 1, higherIndex);
// Merge subparts using a temporary array
mergeData(lowerIndex, middle, higherIndex);
}
}
private void mergeData (int lowerIndex, int middle, int higherIndex) {
for (int i = lowerIndex; i <= higherIndex; i++) {
tempMergedArr[i] = array[i];
}
int i = lowerIndex;
int j = middle + 1;
int k = lowerIndex;
while (i <= middle && j <= higherIndex) {
if (tempMergedArr[i] <= tempMergedArr[j]) {
array[k] = tempMergedArr[i];
i++;
} else {
array[k] = tempMergedArr[j];
j++;
}
k++;
}
while (i <= middle) {
array[k] = tempMergedArr[i];
k++;
i++;
}
}
}Le code ci-dessus produira un tableau trié en sortie.
Sortie :

Le tri par fusion peut être utilisé dans les scénarios suivants :
Les points ci-dessous analysent la complexité du tri par fusion :
Les points ci-dessous comparent le tri par fusion avec d'autres algorithmes :
L'article conclut que le tri par fusion est un concept important à comprendre en matière d'algorithmes.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!