
Classification est une technique d'apprentissage supervisé utilisée en apprentissage automatique et en science des données pour classer les données dans des classes ou des étiquettes prédéfinies. Cela implique la formation d'un modèle pour attribuer des points de données d'entrée à l'une des nombreuses catégories discrètes en fonction de leurs caractéristiques. L'objectif principal de la classification est de prédire avec précision la classe ou la catégorie de nouveaux points de données invisibles.
1. Classification binaire
2. Classification multiclasse
Classificateurs linéaires sont une catégorie d'algorithmes de classification qui utilisent une limite de décision linéaire pour séparer différentes classes dans l'espace des fonctionnalités. Ils font des prédictions en combinant les entités d'entrée via une équation linéaire, représentant généralement la relation entre les entités et les étiquettes de classe cible. L'objectif principal des classificateurs linéaires est de classer efficacement les points de données en trouvant un hyperplan qui divise l'espace des fonctionnalités en classes distinctes.
Régression logistique est une méthode statistique utilisée pour les tâches de classification binaire dans l'apprentissage automatique et la science des données. Il fait partie des classificateurs linéaires et diffère de la régression linéaire en prédisant la probabilité d'occurrence d'un événement en ajustant les données à une courbe logistique.
1. Fonction logistique (fonction sigmoïde)
2. Équation de régression logistique
MLE est utilisé pour estimer les paramètres (coefficients) du modèle de régression logistique en maximisant la probabilité d'observer les données étant donné le modèle.
Équation : Maximiser la fonction log-vraisemblance implique de trouver les paramètres qui maximisent la probabilité d'observer les données.
La fonction de coût dans la régression logistique mesure la différence entre les probabilités prédites et les étiquettes de classe réelles. L'objectif est de minimiser cette fonction pour améliorer la précision prédictive du modèle.
Perte de journal (entropie croisée binaire) :
La fonction de perte de log est couramment utilisée en régression logistique pour les tâches de classification binaire.
Log Perte = -(1/n) * Σ [y * log(ŷ) + (1 - y) * log(1 - ŷ)]
où :
La perte de log pénalise les prédictions qui sont loin de l'étiquette de classe réelle, encourageant le modèle à produire des probabilités précises.
Minimisation des pertes dans la régression logistique consiste à trouver les valeurs des paramètres du modèle qui minimisent la valeur de la fonction de coût. Ce processus est également connu sous le nom d'optimisation. La méthode la plus courante pour minimiser les pertes dans la régression logistique est l'algorithme Gradient Descent.
Gradient Descent est un algorithme d'optimisation itératif utilisé pour minimiser la fonction de coût dans la régression logistique. Il ajuste les paramètres du modèle dans le sens de la descente la plus raide de la fonction de coût.
Étapes de descente de dégradé :
Initialiser les paramètres : Commencez par les valeurs initiales des paramètres du modèle (par exemple, les coefficients w0, w1, ..., wn).
Calculer le gradient : Calculez le gradient de la fonction de coût par rapport à chaque paramètre. Le gradient est la dérivée partielle de la fonction de coût.
Mettre à jour les paramètres : Ajustez les paramètres dans le sens opposé du dégradé. L'ajustement est contrôlé par le taux d'apprentissage (α), qui détermine la taille des pas effectués vers le minimum.
Répéter : Répétez le processus jusqu'à ce que la fonction de coût converge vers une valeur minimale (ou qu'un nombre prédéfini d'itérations soit atteint).
Règle de mise à jour des paramètres :
Pour chaque paramètre wj :
wj = wj - α * (∂/∂wj) Log Perte
où :
La dérivée partielle de la perte log par rapport à wj peut être calculée comme suit :
(∂/∂wj) Log Perte = -(1/n) * Σ [ (yi - ŷi) * xij / (ŷi * (1 - ŷi)) ]
où :
La régression logistique est une technique utilisée pour les tâches de classification binaire, modélisant la probabilité qu'une entrée donnée appartienne à une classe particulière. Cet exemple montre comment mettre en œuvre une régression logistique à l'aide de données synthétiques, évaluer les performances du modèle et visualiser la limite de décision.
1. Importer des bibliothèques
import numpy as np import matplotlib.pyplot as plt from sklearn.model_selection import train_test_split from sklearn.linear_model import LogisticRegression from sklearn.metrics import accuracy_score, confusion_matrix, classification_report
Ce bloc importe les bibliothèques nécessaires à la manipulation des données, au traçage et à l'apprentissage automatique.
2. Générer des exemples de données
np.random.seed(42) # For reproducibility X = np.random.randn(1000, 2) y = (X[:, 0] + X[:, 1] > 0).astype(int)
Ce bloc génère des exemples de données avec deux caractéristiques, où la variable cible y est définie selon que la somme des caractéristiques est supérieure à zéro, simulant un scénario de classification binaire.
3. Diviser l'ensemble de données
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
Ce bloc divise l'ensemble de données en ensembles de formation et de test pour l'évaluation du modèle.
4. Créer et entraîner le modèle de régression logistique
model = LogisticRegression(random_state=42) model.fit(X_train, y_train)
Ce bloc initialise le modèle de régression logistique et l'entraîne à l'aide de l'ensemble de données d'entraînement.
5. Faire des pronostics
y_pred = model.predict(X_test)
Ce bloc utilise le modèle entraîné pour faire des prédictions sur l'ensemble de test.
6. Évaluer le modèle
accuracy = accuracy_score(y_test, y_pred)
conf_matrix = confusion_matrix(y_test, y_pred)
class_report = classification_report(y_test, y_pred)
print(f"Accuracy: {accuracy:.4f}")
print("\nConfusion Matrix:")
print(conf_matrix)
print("\nClassification Report:")
print(class_report)
Sortie :
Accuracy: 0.9950
Confusion Matrix:
[[ 92 0]
[ 1 107]]
Classification Report:
precision recall f1-score support
0 0.99 1.00 0.99 92
1 1.00 0.99 1.00 108
accuracy 0.99 200
macro avg 0.99 1.00 0.99 200
weighted avg 1.00 0.99 1.00 200
Ce bloc calcule et imprime la précision, la matrice de confusion et le rapport de classification, fournissant ainsi un aperçu des performances du modèle.
7. Visualisez la limite de décision
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),
np.arange(y_min, y_max, 0.1))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.figure(figsize=(10, 8))
plt.contourf(xx, yy, Z, alpha=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, alpha=0.8)
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.title("Logistic Regression Decision Boundary")
plt.show()
Ce bloc visualise la limite de décision créée par le modèle de régression logistique, illustrant comment le modèle sépare les deux classes dans l'espace des fonctionnalités.
Sortie :
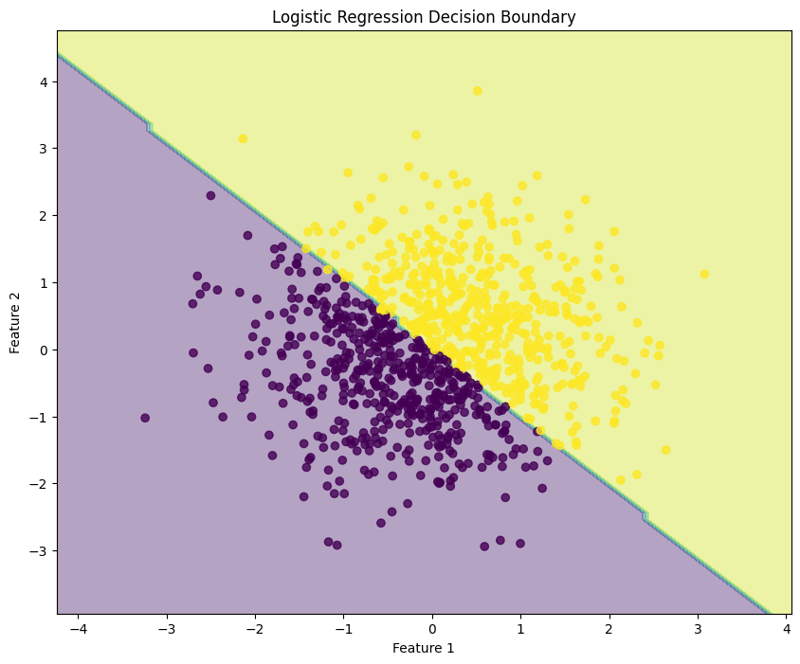
Cette approche structurée montre comment mettre en œuvre et évaluer la régression logistique, fournissant une compréhension claire de ses capacités pour les tâches de classification binaire. La visualisation de la limite de décision facilite l'interprétation des prédictions du modèle.
Logistic regression can also be applied to multiclass classification tasks. This example demonstrates how to implement logistic regression using synthetic data, evaluate the model's performance, and visualize the decision boundary for three classes.
1. Import Libraries
import numpy as np import matplotlib.pyplot as plt from sklearn.model_selection import train_test_split from sklearn.linear_model import LogisticRegression from sklearn.metrics import accuracy_score, confusion_matrix, classification_report
This block imports the necessary libraries for data manipulation, plotting, and machine learning.
2. Generate Sample Data with 3 Classes
np.random.seed(42) # For reproducibility
n_samples = 999 # Total number of samples
n_samples_per_class = 333 # Ensure this is exactly n_samples // 3
# Class 0: Top-left corner
X0 = np.random.randn(n_samples_per_class, 2) * 0.5 + [-2, 2]
# Class 1: Top-right corner
X1 = np.random.randn(n_samples_per_class, 2) * 0.5 + [2, 2]
# Class 2: Bottom center
X2 = np.random.randn(n_samples_per_class, 2) * 0.5 + [0, -2]
# Combine the data
X = np.vstack([X0, X1, X2])
y = np.hstack([np.zeros(n_samples_per_class),
np.ones(n_samples_per_class),
np.full(n_samples_per_class, 2)])
# Shuffle the dataset
shuffle_idx = np.random.permutation(n_samples)
X, y = X[shuffle_idx], y[shuffle_idx]
This block generates synthetic data for three classes located in different regions of the feature space.
3. Split the Dataset
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
This block splits the dataset into training and testing sets for model evaluation.
4. Create and Train the Logistic Regression Model
model = LogisticRegression(random_state=42) model.fit(X_train, y_train)
This block initializes the logistic regression model and trains it using the training dataset.
5. Make Predictions
y_pred = model.predict(X_test)
This block uses the trained model to make predictions on the test set.
6. Evaluate the Model
accuracy = accuracy_score(y_test, y_pred)
conf_matrix = confusion_matrix(y_test, y_pred)
class_report = classification_report(y_test, y_pred)
print(f"Accuracy: {accuracy:.4f}")
print("\nConfusion Matrix:")
print(conf_matrix)
print("\nClassification Report:")
print(class_report)
Output:
Accuracy: 1.0000
Confusion Matrix:
[[54 0 0]
[ 0 65 0]
[ 0 0 81]]
Classification Report:
precision recall f1-score support
0.0 1.00 1.00 1.00 54
1.0 1.00 1.00 1.00 65
2.0 1.00 1.00 1.00 81
accuracy 1.00 200
macro avg 1.00 1.00 1.00 200
weighted avg 1.00 1.00 1.00 200
This block calculates and prints the accuracy, confusion matrix, and classification report, providing insights into the model's performance.
7. Visualize the Decision Boundary
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),
np.arange(y_min, y_max, 0.1))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.figure(figsize=(10, 8))
plt.contourf(xx, yy, Z, alpha=0.4, cmap='RdYlBu')
scatter = plt.scatter(X[:, 0], X[:, 1], c=y, cmap='RdYlBu', edgecolor='black')
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.title("Multiclass Logistic Regression Decision Boundary")
plt.colorbar(scatter)
plt.show()
This block visualizes the decision boundaries created by the logistic regression model, illustrating how the model separates the three classes in the feature space.
Output:

This structured approach demonstrates how to implement and evaluate logistic regression for multiclass classification tasks, providing a clear understanding of its capabilities and the effectiveness of visualizing decision boundaries.
Evaluating a logistic regression model involves assessing its performance in predicting binary or multiclass outcomes. Below are key methods for evaluation:
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy: {accuracy:.4f}')
from sklearn.metrics import confusion_matrix
conf_matrix = confusion_matrix(y_test, y_pred)
print("\nConfusion Matrix:")
print(conf_matrix)
from sklearn.metrics import precision_score
precision = precision_score(y_test, y_pred, average='weighted')
print(f'Precision: {precision:.4f}')
from sklearn.metrics import recall_score
recall = recall_score(y_test, y_pred, average='weighted')
print(f'Recall: {recall:.4f}')
from sklearn.metrics import f1_score
f1 = f1_score(y_test, y_pred, average='weighted')
print(f'F1 Score: {f1:.4f}')
Cross-validation techniques provide a more reliable evaluation of model performance by assessing it across different subsets of the dataset.
from sklearn.model_selection import KFold, cross_val_score
kf = KFold(n_splits=5, shuffle=True, random_state=42)
scores = cross_val_score(model, X, y, cv=kf, scoring='accuracy')
print(f'Cross-Validation Accuracy: {np.mean(scores):.4f}')
from sklearn.model_selection import StratifiedKFold
skf = StratifiedKFold(n_splits=5)
scores = cross_val_score(model, X, y, cv=skf, scoring='accuracy')
print(f'Stratified K-Fold Cross-Validation Accuracy: {np.mean(scores):.4f}')
By utilizing these evaluation methods and cross-validation techniques, practitioners can gain insights into the effectiveness of their logistic regression model and its ability to generalize to unseen data.
Regularization helps mitigate overfitting in logistic regression by adding a penalty term to the loss function, encouraging simpler models. The two primary forms of regularization in logistic regression are L1 regularization (Lasso) and L2 regularization (Ridge).
Concept : La régularisation L2 ajoute une pénalité égale au carré de la grandeur des coefficients à la fonction de perte.
Fonction de perte : La fonction de perte modifiée pour la régression logistique Ridge est exprimée comme :
Perte = -Σ[yi * log(ŷi) + (1 - yi) * log(1 - ŷi)] + λ * Σ(wj^2)
Où :
Effets :
Concept : La régularisation L1 ajoute une pénalité égale à la valeur absolue de la grandeur des coefficients à la fonction de perte.
Fonction de perte : La fonction de perte modifiée pour la régression logistique Lasso peut être exprimée comme :
Perte = -Σ[yi * log(ŷi) + (1 - yi) * log(1 - ŷi)] + λ * Σ|wj|
Où :
Effets :
En appliquant des techniques de régularisation à la régression logistique, les praticiens peuvent améliorer la généralisation du modèle et gérer efficacement le compromis biais-variance.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 Solution au problème selon lequel le système Win7 ne peut pas démarrer
Solution au problème selon lequel le système Win7 ne peut pas démarrer
 utilisation du curseur Oracle
utilisation du curseur Oracle
 Que signifie la liquidation ?
Que signifie la liquidation ?
 Utilisation de la fonction GAMMAINV
Utilisation de la fonction GAMMAINV
 Quelles sont les technologies de collecte de données ?
Quelles sont les technologies de collecte de données ?
 Quels sont les logiciels bureautiques
Quels sont les logiciels bureautiques
 Pourquoi l'imprimante n'imprime-t-elle pas ?
Pourquoi l'imprimante n'imprime-t-elle pas ?
 qu'est-ce que Hadoop
qu'est-ce que Hadoop