Montrez la chaîne causale à LLM et il apprendra les axiomes.
L'IA aide déjà les mathématiciens et les scientifiques à faire des recherches. Par exemple, le célèbre mathématicien Tao Zhexuan a partagé à plusieurs reprises son expérience de recherche et d'exploration avec l'aide de GPT et d'autres outils d'IA. Pour que l’IA soit compétitive dans ces domaines, des capacités de raisonnement causal solides et fiables sont essentielles. La recherche présentée dans cet article a révélé que les modèles Transformer formés sur des démonstrations de l'axiome de transitivité causale pour les petits graphes peuvent se généraliser à l'axiome de transitivité pour les grands graphes. En d'autres termes, si Transformer apprend à effectuer un raisonnement causal simple, il peut être utilisé pour un raisonnement causal plus complexe. Le cadre de formation aux axiomes proposé par l'équipe est un nouveau paradigme pour l'apprentissage du raisonnement causal basé sur des données passives, qui peut être utilisé pour apprendre des axiomes arbitraires tant que la démonstration est suffisante. Le raisonnement causal peut être défini comme un ensemble de processus de raisonnement conformes à des axiomes ou à des règles prédéfinies spécifiquement pour la causalité. Par exemple, les règles de séparation d (séparation dirigée) et de calcul peuvent être considérées comme des axiomes, tandis que les spécifications d'un ensemble de collisionneurs ou d'un ensemble de portes dérobées peuvent être considérées comme des règles dérivées des axiomes. De manière générale, l'inférence causale utilise des données qui correspondent aux variables d'un système. Des axiomes ou des règles peuvent être intégrés dans des modèles d'apprentissage automatique sous la forme de biais inductifs via la régularisation, l'architecture du modèle ou la sélection de variables spécifiques. Sur la base des différences dans les types de données disponibles (données d'observation, données d'intervention, données contrefactuelles), « l'échelle causale » proposée par Judea Pearl définit les types possibles d'inférence causale. Étant donné que les axiomes sont la pierre angulaire de la causalité, nous ne pouvons nous empêcher de nous demander si nous pouvons utiliser directement des modèles d'apprentissage automatique pour apprendre des axiomes. Autrement dit, que se passerait-il si la manière d'apprendre des axiomes n'était pas d'apprendre des données obtenues via un processus de génération de données, mais directement d'apprendre des démonstrations symboliques d'axiomes (et donc d'apprendre le raisonnement causal) ? Par rapport aux modèles causals spécifiques à une tâche construits à l'aide de distributions de données spécifiques, un tel modèle présente un avantage : il peut réaliser une inférence causale dans une variété de différents scénarios en aval. Cette question devient importante à mesure que les modèles linguistiques acquièrent la capacité d’apprendre des données symboliques exprimées en langage naturel. En fait, certaines recherches récentes ont évalué si les grands modèles de langage (LLM) sont capables d'effectuer une inférence causale en créant des critères qui codent les problèmes d'inférence causale en langage naturel. Des équipes de recherche de Microsoft, du MIT et de l'Indian Institute of Technology Hyderabad (IIT Hyderabad) ont également franchi une étape importante dans cette direction : en proposant une méthode pour apprendre le raisonnement causal grâce à un entraînement axiomatique . 
- Titre de l'article : Enseigner le raisonnement causal aux transformateurs grâce à la formation axiomatique
- Adresse de l'article : https://arxiv.org/pdf/2407.07612
Ils assument, L'axiome causal peut être exprimé sous la forme du tuple symbolique suivant 〈prémisse, hypothèse, résultat〉. Parmi eux, l'hypothèse fait référence à l'hypothèse, c'est-à-dire qu'une prémisse causale est la prémisse, qui fait référence à toute information pertinente utilisée pour déterminer si la déclaration est « vraie » ; Le résultat peut être un simple « oui » ou « non ». Par exemple, l'axiome du collisionneur de l'article « Les grands modèles de langage peuvent-ils déduire une causalité à partir d'une corrélation ? » peut être exprimé comme suit :  , et la conclusion est « oui ». Sur la base de ce modèle, un grand nombre de tuples synthétiques peuvent être générés en modifiant les noms de variables, les numéros de variables, l'ordre des variables, etc. Afin d'utiliser Transformer pour apprendre les axiomes causals et mettre en œuvre la formation aux axiomes, l'équipe a utilisé les méthodes suivantes pour construire des ensembles de données, des fonctions de perte et des intégrations de positions. Formation axiomatique : ensemble de données, fonction de perte et compilation de positionsBasée sur un axiome spécifique, "l'hypothèse" peut être mappée à une étiquette appropriée basée sur la "prémisse" ( Oui ou non). Pour créer l'ensemble de données d'entraînement, l'équipe énumère tous les tuples possibles {(P, H, L)}_N sous des paramètres de variables spécifiques X, Y, Z, A, où P est la prémisse et H est l'hypothèse, L est l'étiquette (Oui ou non). Étant donné une prémisse P basée sur un diagramme de causalité, si l'hypothèse P peut être dérivée en utilisant un axiome spécifique (une ou plusieurs fois), alors l'étiquette L est Oui, sinon c'est Non ; Par exemple, supposons que le graphe causal réel sous-jacent d'un système ait une topologie en chaîne : X_1 → X_2 → X_3 →・・・→ X_n. Alors, une prémisse possible est X_1 → X_2 ∧ X_2 → X_3, alors supposons X_1 → Les axiomes ci-dessus peuvent être utilisés de manière inductive plusieurs fois pour générer des tuples de formation plus complexes. Pour la configuration de la formation, construisez un ensemble de données synthétiques D en utilisant N instances d'axiome générées par l'axiome de transitivité. Chaque instance de D est construite sous la forme (P_i, H_ij, L_ij),
, et la conclusion est « oui ». Sur la base de ce modèle, un grand nombre de tuples synthétiques peuvent être générés en modifiant les noms de variables, les numéros de variables, l'ordre des variables, etc. Afin d'utiliser Transformer pour apprendre les axiomes causals et mettre en œuvre la formation aux axiomes, l'équipe a utilisé les méthodes suivantes pour construire des ensembles de données, des fonctions de perte et des intégrations de positions. Formation axiomatique : ensemble de données, fonction de perte et compilation de positionsBasée sur un axiome spécifique, "l'hypothèse" peut être mappée à une étiquette appropriée basée sur la "prémisse" ( Oui ou non). Pour créer l'ensemble de données d'entraînement, l'équipe énumère tous les tuples possibles {(P, H, L)}_N sous des paramètres de variables spécifiques X, Y, Z, A, où P est la prémisse et H est l'hypothèse, L est l'étiquette (Oui ou non). Étant donné une prémisse P basée sur un diagramme de causalité, si l'hypothèse P peut être dérivée en utilisant un axiome spécifique (une ou plusieurs fois), alors l'étiquette L est Oui, sinon c'est Non ; Par exemple, supposons que le graphe causal réel sous-jacent d'un système ait une topologie en chaîne : X_1 → X_2 → X_3 →・・・→ X_n. Alors, une prémisse possible est X_1 → X_2 ∧ X_2 → X_3, alors supposons X_1 → Les axiomes ci-dessus peuvent être utilisés de manière inductive plusieurs fois pour générer des tuples de formation plus complexes. Pour la configuration de la formation, construisez un ensemble de données synthétiques D en utilisant N instances d'axiome générées par l'axiome de transitivité. Chaque instance de D est construite sous la forme (P_i, H_ij, L_ij),  , où n est le nombre de nœuds dans chaque i-ième prémisse. P est la prémisse, c'est-à-dire une expression en langage naturel d'une certaine structure causale (telle que X provoque Y, Y provoque Z) suivie de la question H (telle que X provoque Y ? L est l'étiquette (Oui) ; ou pas). Ce formulaire couvre effectivement toutes les paires de nœuds pour chaque chaîne unique dans un graphe causal donné. Étant donné un ensemble de données, la fonction de perte est définie en fonction de l'étiquette de vérité terrain de chaque tuple, exprimée comme suit :
, où n est le nombre de nœuds dans chaque i-ième prémisse. P est la prémisse, c'est-à-dire une expression en langage naturel d'une certaine structure causale (telle que X provoque Y, Y provoque Z) suivie de la question H (telle que X provoque Y ? L est l'étiquette (Oui) ; ou pas). Ce formulaire couvre effectivement toutes les paires de nœuds pour chaque chaîne unique dans un graphe causal donné. Étant donné un ensemble de données, la fonction de perte est définie en fonction de l'étiquette de vérité terrain de chaque tuple, exprimée comme suit :  L'analyse montre que par rapport à la prédiction de jeton suivante, en utilisant ces pertes peut donner des résultats prometteurs. En plus des fonctions d'entraînement et de perte, le choix de l'encodage positionnel est également un autre facteur important. Le codage positionnel peut fournir des informations clés sur la position absolue et relative d'un jeton dans une séquence. Le célèbre article "L'attention est tout ce dont vous avez besoin" propose une stratégie de codage de position absolue qui utilise des fonctions périodiques (fonctions sinus ou cosinus) pour initialiser ces codes. Le codage de position absolue peut fournir certaines valeurs pour toutes les positions de n'importe quelle longueur de séquence. Cependant, certaines recherches montrent que le codage de position absolue est difficile à réaliser avec la tâche de généralisation de longueur de Transformer. Dans la variante APE apprenable, chaque intégration de position est initialisée et entraînée de manière aléatoire à l'aide du modèle. Cette méthode a du mal avec les séquences plus longues que celles de l'entraînement car les nouvelles intégrations de positions ne sont toujours pas entraînées et non initialisées. Fait intéressant, des découvertes récentes ont montré que la suppression des incorporations de position dans les modèles autorégressifs peut améliorer la capacité de généralisation de longueur du modèle, et le mécanisme d'attention pendant le décodage autorégressif est suffisant pour coder les informations de position. L’équipe a utilisé différents codages de position pour comprendre leur impact sur la généralisation dans les tâches causales, notamment le codage de position apprenable (LPE), le codage de position sinusoïdale (SPE) et l’absence de codage de position (NoPE).Afin d'améliorer la capacité de généralisation du modèle, l'équipe a également utilisé des perturbations de données, notamment des perturbations de longueur, de nom de nœud, d'ordre de chaîne et d'état de branche. La question suivante se pose : si un modèle est formé à l'aide de ces données, le modèle peut-il apprendre à appliquer cet axiome à de nouveaux scénarios ? Pour répondre à cette question, l'équipe a formé un modèle Transformer à partir de zéro en utilisant cette démonstration symbolique de l'axiome causalement indépendant. Pour évaluer ses performances de généralisation, ils se sont entraînés sur une simple chaîne d'axiomes causalement indépendante de taille 3 à 6 nœuds, puis ont testé plusieurs aspects différents des performances de généralisation, y compris les performances de généralisation de longueur (chaînes de taille 7 à 15), généralisation des noms (noms de variables plus longs), généralisation séquentielle (chaînes avec bords inversés ou nœuds mélangés), généralisation structurelle (graphiques avec branches) ). La figure 1 illustre comment évaluer la généralisation structurelle de Transformer.
L'analyse montre que par rapport à la prédiction de jeton suivante, en utilisant ces pertes peut donner des résultats prometteurs. En plus des fonctions d'entraînement et de perte, le choix de l'encodage positionnel est également un autre facteur important. Le codage positionnel peut fournir des informations clés sur la position absolue et relative d'un jeton dans une séquence. Le célèbre article "L'attention est tout ce dont vous avez besoin" propose une stratégie de codage de position absolue qui utilise des fonctions périodiques (fonctions sinus ou cosinus) pour initialiser ces codes. Le codage de position absolue peut fournir certaines valeurs pour toutes les positions de n'importe quelle longueur de séquence. Cependant, certaines recherches montrent que le codage de position absolue est difficile à réaliser avec la tâche de généralisation de longueur de Transformer. Dans la variante APE apprenable, chaque intégration de position est initialisée et entraînée de manière aléatoire à l'aide du modèle. Cette méthode a du mal avec les séquences plus longues que celles de l'entraînement car les nouvelles intégrations de positions ne sont toujours pas entraînées et non initialisées. Fait intéressant, des découvertes récentes ont montré que la suppression des incorporations de position dans les modèles autorégressifs peut améliorer la capacité de généralisation de longueur du modèle, et le mécanisme d'attention pendant le décodage autorégressif est suffisant pour coder les informations de position. L’équipe a utilisé différents codages de position pour comprendre leur impact sur la généralisation dans les tâches causales, notamment le codage de position apprenable (LPE), le codage de position sinusoïdale (SPE) et l’absence de codage de position (NoPE).Afin d'améliorer la capacité de généralisation du modèle, l'équipe a également utilisé des perturbations de données, notamment des perturbations de longueur, de nom de nœud, d'ordre de chaîne et d'état de branche. La question suivante se pose : si un modèle est formé à l'aide de ces données, le modèle peut-il apprendre à appliquer cet axiome à de nouveaux scénarios ? Pour répondre à cette question, l'équipe a formé un modèle Transformer à partir de zéro en utilisant cette démonstration symbolique de l'axiome causalement indépendant. Pour évaluer ses performances de généralisation, ils se sont entraînés sur une simple chaîne d'axiomes causalement indépendante de taille 3 à 6 nœuds, puis ont testé plusieurs aspects différents des performances de généralisation, y compris les performances de généralisation de longueur (chaînes de taille 7 à 15), généralisation des noms (noms de variables plus longs), généralisation séquentielle (chaînes avec bords inversés ou nœuds mélangés), généralisation structurelle (graphiques avec branches) ). La figure 1 illustre comment évaluer la généralisation structurelle de Transformer. 
Plus précisément, ils ont formé un modèle basé sur un décodeur avec 67 millions de paramètres basé sur l'architecture GPT-2. Le modèle comporte 12 couches d'attention, 8 têtes d'attention et 512 dimensions d'intégration. Ils ont formé le modèle à partir de zéro sur chaque ensemble de données de formation. Pour comprendre l'impact de l'intégration de position, ils ont également étudié trois paramètres d'intégration de position : le codage de position sinusoïdale (SPE), le codage de position apprenable (LPE) et l'absence de codage de position (NoPE). Les résultats sont présentés dans le tableau 1, la figure 3 et la figure 4. 
Le Tableau 1 donne la précision des différents modèles lorsqu'ils sont évalués sur des chaînes causales plus larges non observées lors de l'entraînement. On peut constater que les performances du nouveau modèle TS2 (NoPE) sont comparables à celles de l’échelle GPT-4 à plusieurs milliards de paramètres. La figure 3 représente les résultats de l'évaluation de la capacité de généralisation sur des séquences causales avec des noms de nœuds plus longs (plus longs que l'ensemble d'entraînement) et l'impact de différentes intégrations de positions. 
La figure 4 évalue la capacité de généralisation sur des séquences causales invisibles plus longues. 
Ils ont découvert que les modèles formés sur des chaînes simples peuvent se généraliser à de multiples applications d'axiomes sur des chaînes plus grandes, mais ne peuvent pas se généraliser à des scénarios plus complexes tels que la généralisation séquentielle ou structurelle. Cependant, si le modèle est formé sur un ensemble de données mixte composé de chaînes simples ainsi que de chaînes avec des bords inversés aléatoires, le modèle se généralise bien à divers scénarios d'évaluation. En élargissant les résultats sur la généralisation de la longueur sur les tâches de PNL, ils ont découvert l'importance des intégrations positionnelles pour assurer la généralisation causale sur la longueur et d'autres dimensions. Leur modèle le plus performant ne comportait aucun codage de position, mais ils ont également constaté que le codage sinusoïdal fonctionnait bien dans certains cas. Cette méthode de formation aux axiomes peut également être généralisée à un problème plus difficile, comme le montre la figure 5. Autrement dit, sur la base de prémisses contenant des déclarations d'indépendance statistique, l'objectif de la tâche est de discerner la corrélation de la causalité. La résolution de cette tâche nécessite la connaissance de plusieurs axiomes, notamment la séparation d et les propriétés de Markov. 
L'équipe a généré des données d'entraînement synthétiques en utilisant la même méthode que ci-dessus, puis a formé un modèle. Il a été constaté que le Transformer formé sur une démonstration de tâche contenant 3 à 4 variables pouvait apprendre à résoudre des problèmes contenant 5 variables Map. Tâches. Et sur cette tâche, le modèle est plus précis que les LLM plus grands tels que GPT-4 et Gemini Pro. 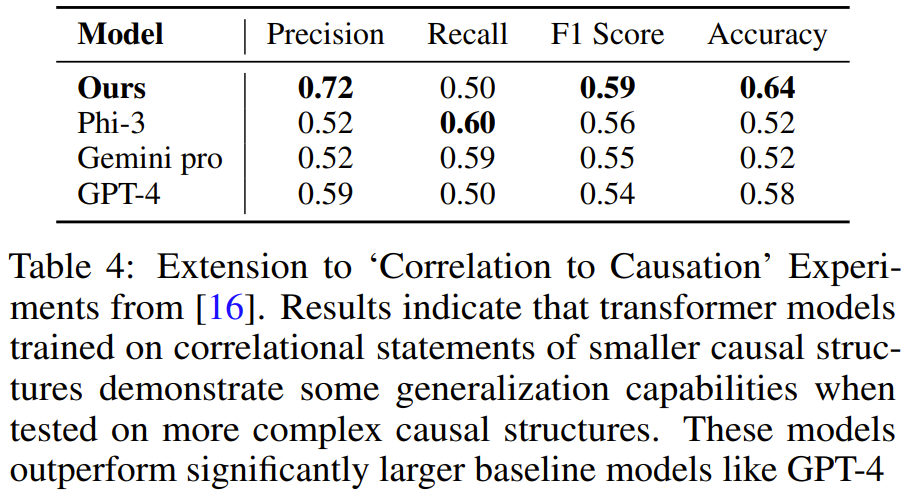
L'équipe a déclaré : "Notre recherche fournit un nouveau paradigme pour les modèles d'enseignement permettant d'apprendre le raisonnement causal à travers des démonstrations symboliques d'axiomes, que nous appelons formation axiomatique et formation de cette méthode. La procédure est générale : aussi longue." comme un axiome peut être exprimé sous forme de tuples symboliques, il peut être appris en utilisant cette méthode. Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!


 , et la conclusion est « oui ».
, et la conclusion est « oui ».  , où n est le nombre de nœuds dans chaque i-ième prémisse. P est la prémisse, c'est-à-dire une expression en langage naturel d'une certaine structure causale (telle que X provoque Y, Y provoque Z) suivie de la question H (telle que X provoque Y ? L est l'étiquette (Oui) ; ou pas). Ce formulaire couvre effectivement toutes les paires de nœuds pour chaque chaîne unique dans un graphe causal donné.
, où n est le nombre de nœuds dans chaque i-ième prémisse. P est la prémisse, c'est-à-dire une expression en langage naturel d'une certaine structure causale (telle que X provoque Y, Y provoque Z) suivie de la question H (telle que X provoque Y ? L est l'étiquette (Oui) ; ou pas). Ce formulaire couvre effectivement toutes les paires de nœuds pour chaque chaîne unique dans un graphe causal donné.  L'analyse montre que par rapport à la prédiction de jeton suivante, en utilisant ces pertes peut donner des résultats prometteurs.
L'analyse montre que par rapport à la prédiction de jeton suivante, en utilisant ces pertes peut donner des résultats prometteurs. 




