Étude de cas : Calcul des factorielles

Une méthode récursive est une méthode qui s'appelle elle-même. De nombreuses fonctions mathématiques sont définies par récursion. Commençons par un exemple simple. La factorielle d'un nombre n peut être définie récursivement comme suit :

0 ! = 1;
n! = n × (n - 1) !; n> 0

Comment trouver n! pour un n donné ? Trouver 1! est facile, car vous savez que 0! vaut 1, et 1! vaut 1 × 0 !. En supposant que vous connaissez (n - 1)!, vous pouvez obtenir n! immédiatement en utilisant n × (n - 1)!. Ainsi, le problème du calcul n! se réduit au calcul (n - 1)!. Lors du calcul de (n - 1)!, vous pouvez appliquer la même idée de manière récursive jusqu'à ce que n soit réduit à 0.

Soit factorial(n) la méthode de calcul de n!. Si vous appelez la méthode avec n = 0, elle renvoie immédiatement le résultat. La méthode sait résoudre le cas le plus simple, appelé cas de base ou condition d'arrêt. Si vous appelez la méthode avec n > 0, il réduit le problème en un sous-problème de calcul de la factorielle de n - 1. Le sous-problème est essentiellement le même que le problème d'origine, mais il est plus simple ou plus petit. Étant donné que le sous-problème a la même propriété que le problème d'origine, vous pouvez appeler la méthode avec un argument différent, appelé appel récursif.

L'algorithme récursif de calcul factoriel(n) peut être simplement décrit comme suit :

si (n == 0)
renvoie 1 ;
d'autre
return n * factorielle(n - 1);

Un appel récursif peut entraîner de nombreux autres appels récursifs, car la méthode continue de diviser un sous-problème en nouveaux sous-problèmes. Pour qu'une méthode récursive se termine, le problème doit finalement être réduit à un cas d'arrêt, auquel cas la méthode renvoie un résultat à son appelant. L'appelant effectue ensuite un calcul et renvoie le résultat à son propre appelant. Ce processus se poursuit jusqu'à ce que le résultat soit renvoyé à l'appelant d'origine. Le problème d'origine peut maintenant être résolu en multipliant n par le résultat de factorielle (n - 1).

Le code ci-dessous donne un programme complet qui invite l'utilisateur à saisir un entier non négatif et affiche la factorielle du nombre.

La méthode factorielle (lignes 17 à 22) est essentiellement une traduction directe de la définition mathématique récursive de la factorielle en code Java. L'appel à factorial est récursif car il s'appelle lui-même. Le paramètre passé à factorial est décrémenté jusqu'à atteindre le cas de base de 0.

Vous voyez comment écrire une méthode récursive. Comment fonctionne la récursivité en coulisses ? La figure ci-dessous illustre l'exécution des appels récursifs, commençant par n = 4.

L'utilisation de l'espace de pile pour les appels récursifs est illustrée dans la figure ci-dessous.

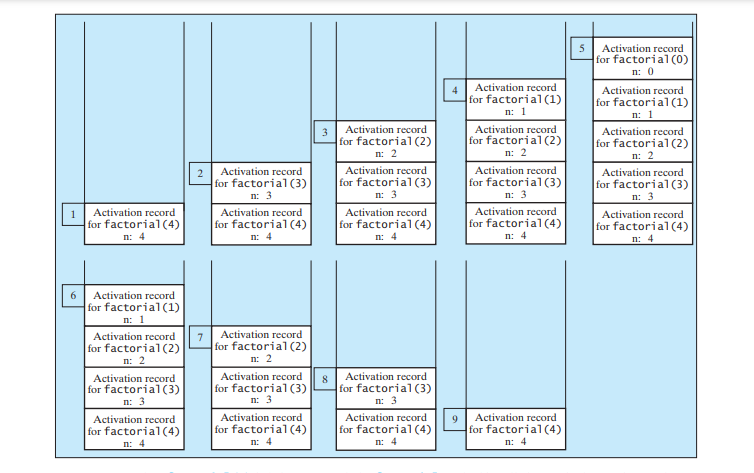
Il est plus simple et plus efficace d'implémenter la méthode factorielle à l'aide d'une boucle. Cependant, nous utilisons ici la méthode récursive factorielle pour démontrer le concept de récursion. Plus loin dans ce chapitre, nous présenterons quelques problèmes intrinsèquement récursifs et difficiles à résoudre sans utiliser la récursivité.

Si la récursivité ne réduit pas le problème de manière à lui permettre de finalement converger vers le cas de base ou si aucun cas de base n'est spécifié, une récursivité infinie peut se produire. Par exemple, supposons que vous écriviez par erreur la méthode factorielle comme suit :

factorielle longue statique publique (int n) {
return n * factorielle(n - 1);
>

La méthode s'exécute à l'infini et provoque une StackOverflowError.

L'exemple discuté dans cette section montre une méthode récursive qui s'appelle elle-même. C'est ce qu'on appelle la récursivité directe. Il est également possible de créer une récursion indirecte. Cela se produit lorsque la méthode A appelle la méthode B, qui à son tour appelle la méthode A. Il peut même y avoir plusieurs autres méthodes impliquées dans la récursivité. Par exemple, la méthode A invoque la méthode B, qui invoque la méthode C, qui invoque la méthode A.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!