Neural network, as the basis of deep learning technology, has achieved effective results in many application fields. In practice, network architecture can significantly affect learning efficiency. A good neural network architecture can incorporate prior knowledge of the problem, establish network training, and improve computing efficiency. Currently, classic network architecture design methods include manual design, neural network architecture search (NAS) [1], and optimization-based network design methods [2]. Artificially designed network architectures such as ResNet, etc.; neural network architecture search searches for the best network structure in the search space through search or reinforcement learning; a mainstream paradigm in optimization-based design methods is algorithm unrolling. This method usually designs the network structure from the perspective of optimization algorithm with an explicit objective function. These methods design the network structure from the perspective of the optimization algorithm while designing the network structure from the perspective of the optimization algorithm.
Most of the current classical neural network architecture designs ignore the universal approximation of the network - this is one of the key factors for the powerful performance of neural networks. Therefore, these design methods lose the a priori performance guarantee of the network to a certain extent. Although the two-layer neural network has universal approximation properties when the width tends to infinity [3], in practice, we can usually only consider network structures with limited width, and the results of performance analysis in this area are very limited. In fact, it is difficult to consider the universal approximation property in network design, whether it is heuristic artificial design or black-box neural network architecture search. Although optimization-based neural network design is relatively more interpretable, it usually requires an obvious objective function, which results in a limited variety of designed network structures and limits its application scope. How to systematically design neural network architectures with universal approximation properties remains an important issue.
The team of Professor Lin Zhouchen of Peking University proposed a neural network architecture based on optimization algorithm design tools. This method combines the gradient-based first-order optimization algorithm with the hash-based second-order optimization. The combination of algorithms improves the training speed and convergence performance, and enhances the robustness guarantee of the neural network. This neural network module can also be used with existing modularity-based network design methods and continues to improve model performance. Recently, they analyzed the approximation properties of neural network differential equations (NODE) and proved that cross-layer connected neural networks have universal approximation properties. They also used the proposed framework to design variant networks such as ConvNext and ViT, and achieved results that exceeded the baseline. . The paper was accepted by TPAMI, the top artificial intelligence journal.
Traditional based Optimized neural network design methods often start from an objective function with an explicit expression, use a specific optimization algorithm to solve it, and then map the optimization results to a neural network structure. For example, the famous LISTA-NN uses the LISTA algorithm to solve the LASSO problem. The resulting explicit expression converts the optimization results into a neural network structure [4]. This method has a strong dependence on the explicit expression of the objective function, so the resulting network structure can only be optimized for the explicit expression of the objective function, and there is a risk of designing assumptions that do not conform to the actual situation. Some researchers try to design the network structure by customizing the objective function and then using methods such as algorithm expansion, but they also require assumptions such as weight rebinding that may not necessarily meet the assumptions in actual situations. Therefore, some researchers have proposed using evolutionary algorithms based on neural networks to search for network architecture to obtain a more reasonable network structure.
The updated format of the network architecture design scheme should follow the idea of from the first-order optimization algorithm to the closer point algorithm and carry out gradual optimization. For example, the Euler angle algorithm can be changed to the quaternion algorithm, or a more efficient iterative algorithm can be used to approximate the solution. The updated format should consider increasing calculation accuracy and improving operating efficiency.
where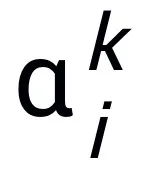
and
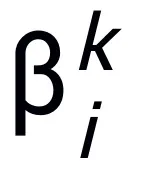represent the (step length) coefficient at the kth step update, and then replace the gradient term with the learnable module T in the neural network, then Obtain the skeleton of the L-layer neural network:
The overall method framework is shown in Figure 1.
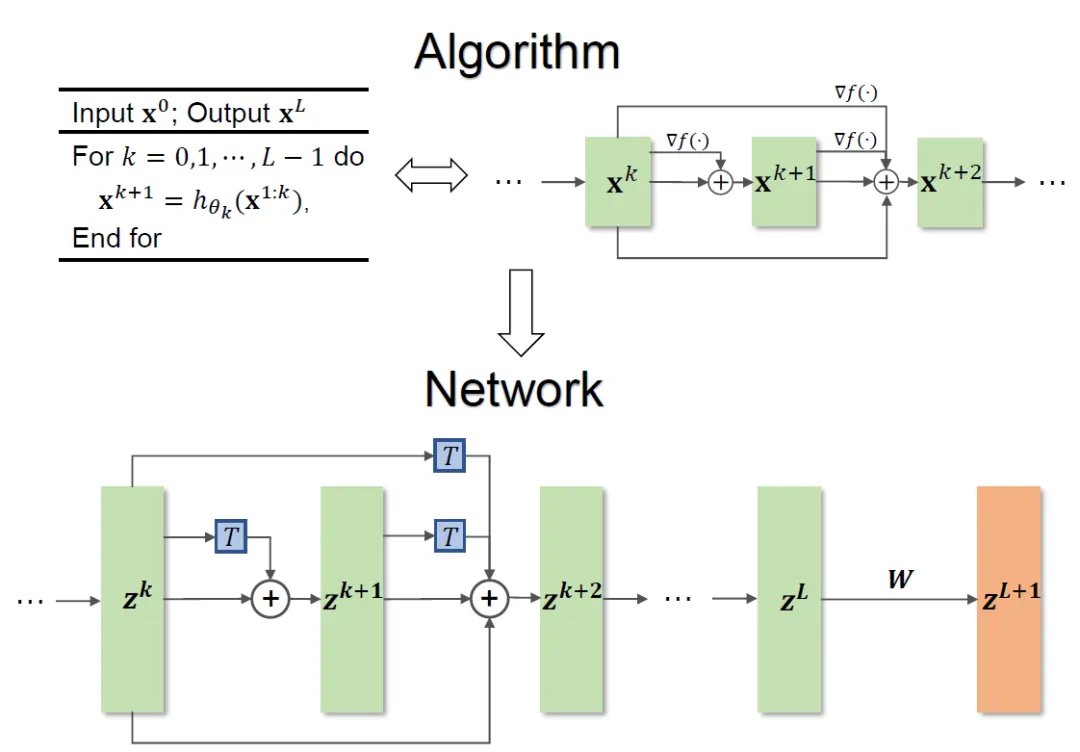
Figure 1 Network design illustration
The method proposed in the paper can inspire the design of ResNet, DenseNet, etc. Classic network, and solves the problem that traditional methods based on optimization design of network architecture are limited to specific objective functions.
Module selection and architectural details
The network module T designed by this method only requires a two-layer network structure, that is,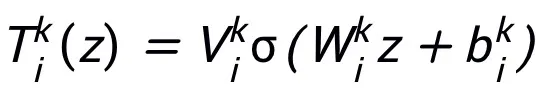
, as its substructure, it can be guaranteed that the designed network has universal approximation properties, in which thewidth of the layer expressed is limited(that is, it does not randomly (increases with the improvement of approximation accuracy), the universal approximation properties of the entire network are not obtained by widening the
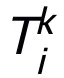layers. Module T can be the pre-activation block widely used in ResNet, or it can be the structure of the attention feed-forward layer in Transformer. The activation function in T can be common activation functions such as ReLU, GeLU, Sigmoid, etc. Corresponding normalization layers can also be added in according to specific tasks. In addition, when
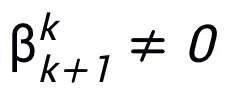, the designed network is an implicit network [5]. You can use fixed point iteration method to approximate the implicit format, or use implicit differentiation method to solve the gradient. renew.
Design more networks through equivalent representation
This method does not require that the same algorithm can only correspond to one Structure, on the contrary, this method can use the equivalent representation of the optimization problem to design more network architectures, reflecting its flexibility. For example, the linearized alternating direction multiplier method is often used to solve constrained optimization problems: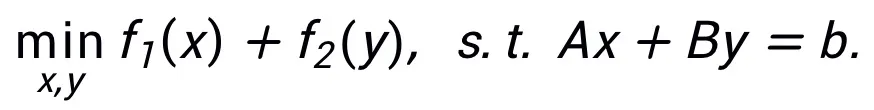
#The inspired network structure can be seen in Figure 2.
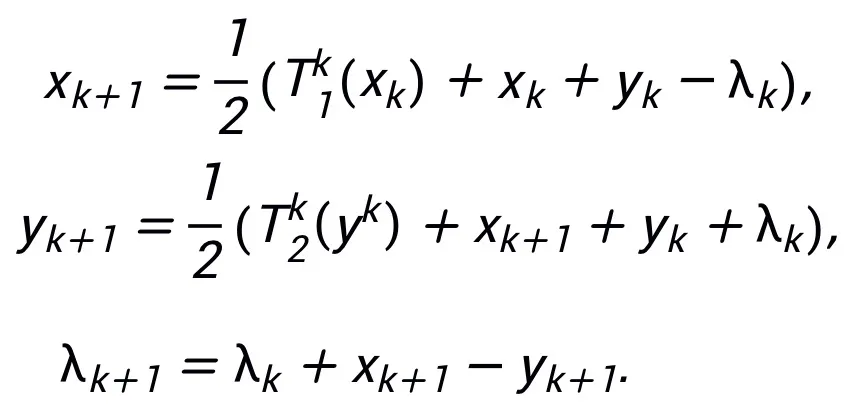
Figure 2 Network structure inspired by linearized alternating direction multiplier method
Inspiration The network has universal approximation properties
The network architecture designed by this method can prove that, under the condition that the module meets the previous conditions and the optimization algorithm (in general) is stable and convergent, the neural network inspired by any first-order optimization algorithm can perform in high-dimensional The continuous function space has universal approximation properties, and the approximation speed is given. For the first time, the paper proves the universal approximation properties of neural networks with general cross-layer connections under thelimited widthsetting (previous research basically focused on FCNN and ResNet, see Table 1). The main theorem of the paper can be briefly described As follows:
Main theorem (short version): Suppose
Ais a gradient type First-order optimization algorithm. If algorithm A has the update format in formula (1) and satisfies the convergence condition (common step size selections for optimization algorithms all satisfy the convergence condition. If they are all learnable in the heuristic network, this condition is not required) , then a neural network inspired by the algorithm:
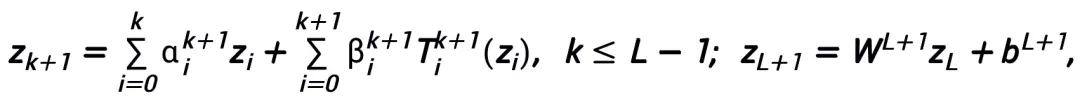
In continuous (vector-valued) function space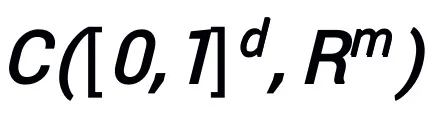
And it has universal approximation properties under the norm
, where the learnable module T only needs to contain a two-layer structure of the form
(σ can be a commonly used activation function ) as its substructure.
Commonly used T structures are:
1) In convolutional networks, pre-activation block: BN-ReLU-Conv-BN -ReLU-Conv (z),
##2) Transformer: Attn (z) MLP (z Attn (z)).
The proof of the main theorem makes use of the universal approximation property of NODE and the convergence property of the linear multi-step method. The core is to prove that the network structure inspired by the optimization algorithm corresponds to the discretization of continuous NODE by a convergent linear multi-step method, so that The inspired network “inherits” the approximation capabilities of NODE. In the proof, the paper also gives the approximation speed of NODE to approximate a continuous function in d-dimensional space, which solves a remaining problem of the previous paper [6].
Table 1 Previous research on the properties of universal approximation basically focused on FCNN and ResNet
The paper uses the proposed network architecture design framework to design 8 explicit networks and 3 implicit networks (called OptDNN). The network information is shown in Table 2, and is nested in Experiments were conducted on problems such as ring separation, function approximation and image classification. The paper also uses ResNet, DenseNet, ConvNext and ViT as baselines, uses the proposed method to design an improved OptDNN, and conducts experiments on the problem of image classification, considering the two indicators of accuracy and FLOPs.
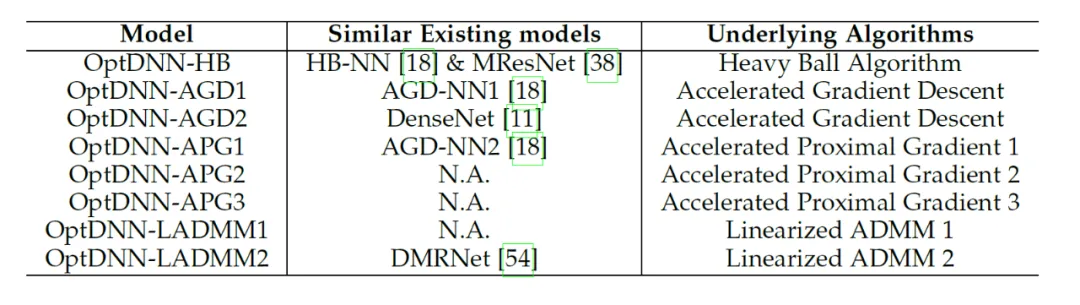
Table 2 Relevant information of the designed network
First, OptDNN separates and Experiments are conducted on two problems of function approximation to verify its universal approximation properties. In the function approximation problem, the approximation parity function and Talgarsky function are considered respectively. The former can be expressed as a binary classification problem, and the latter is a regression problem. Both problems are difficult to be approximated by shallow networks. The experimental results of OptDNN in nested ring separation are shown in Figure 3, and the experimental results in function approximation are shown in Figure 3. OptDNN not only achieved good separation/approximation results, but also achieved greater results than ResNet as the baseline. The classification interval and smaller regression error are enough to verify the universal approximation properties of OptDNN.
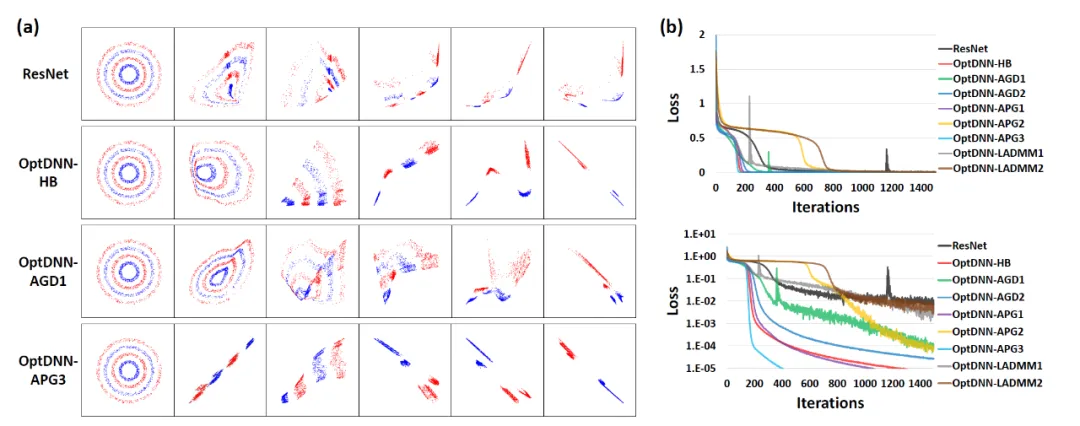
Figure 3 OptNN approximation parity function
# #Figure 4 OptNN approximating the Talgarsky function
Then, OptDNN conducted experiments on the image classification task on the CIFAR data set under two settings: wide-shallow and narrow-deep. The results See Tables 3 and 4. The experiments were all conducted under strong data augmentation settings. It can be seen that some OptDNN achieved smaller error rates than ResNet at the same or even smaller FLOPs overhead. The paper also conducted experiments under ResNet and DenseNet settings and achieved similar experimental results.
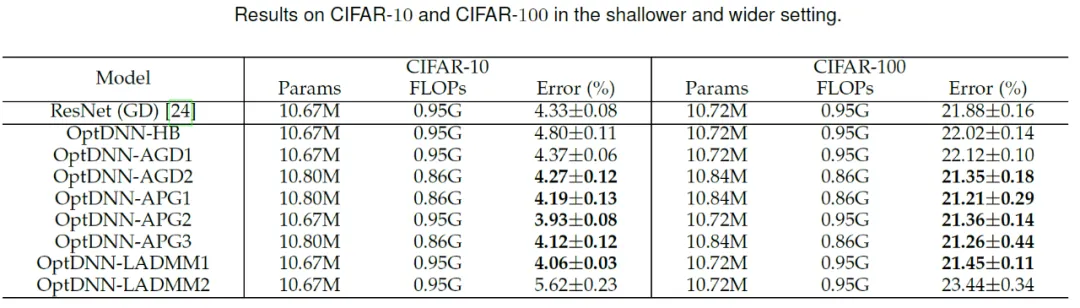
Table 3 Experimental results of OptDNN under wide-shallow settings
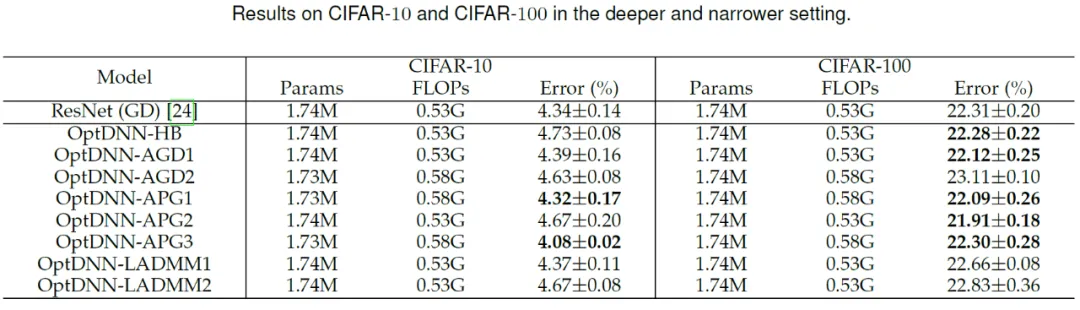
Table 4 Experimental results of OptDNN in narrow-deep settings
The paper further selects the OptDNN-APG2 network that has performed well before, and further improves the performance of ConvNext and ViT. Experiments were conducted on the ImageNet data set under the following settings. The network structure of OptDNN-APG2 is shown in Figure 5, and the experimental results are shown in Tables 5 and 6. OptDNN-APG2 achieved an accuracy rate exceeding that of equal-width ConvNext and ViT, further verifying the reliability of this architecture design method.
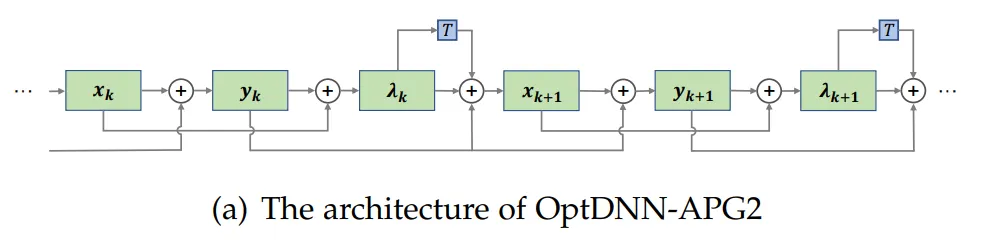
Figure 5 Network structure of OptDNN-APG2
Table 5 Performance comparison of OptDNN-APG2 on ImageNet
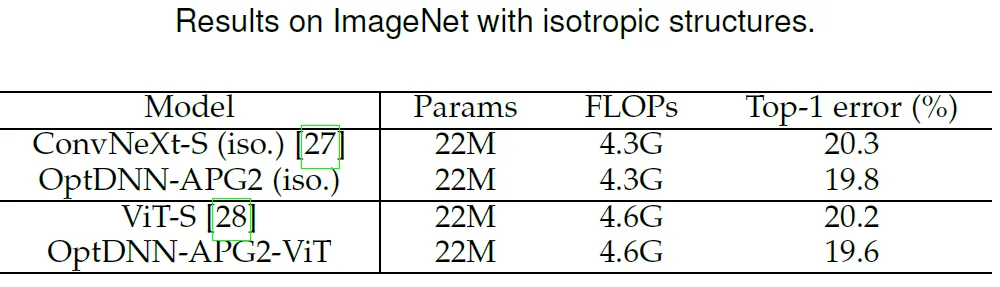
Table 6 Performance comparison of OptDNN-APG2 with isotropic ConvNeXt and ViT
Finally, the paper designed three implicit networks based on algorithms such as Proximal Gradient Descent and FISTA, and conducted experiments on the CIFAR data set with explicit ResNet and some commonly used implicit networks. For comparison, the experimental results are shown in Table 7. All three implicit networks achieved experimental results comparable to advanced implicit networks, which also illustrates the flexibility of the method.
Table 7 Performance comparison of implicit networks
Neural network architecture design is one of the core issues in deep learning. The paper proposes a unified framework for using first-order optimization algorithms to design neural network architectures with universal approximation properties, and expands the method based on the optimization design network architecture paradigm. This method can be combined with most existing architecture design methods that focus on network modules, and an efficient model can be designed with almost no increase in computational effort. In terms of theory, the paper proves that the network architecture induced by convergent optimization algorithms has universal approximation properties under mild conditions, and bridges the representation capabilities of NODE and general cross-layer connection networks. This method is also expected to be combined with NAS, SNN architecture design and other fields to design more efficient network architecture.
The above is the detailed content of Inspired by the first-order optimization algorithm, Peking University Lin Zhouchen's team proposed a design method for neural network architecture with universal approximation properties. For more information, please follow other related articles on the PHP Chinese website!
![[Web front-end] Node.js quick start](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
