The diffusion model opens a new era of generative models with its excellent performance in image generation. Large models such as Stable Diffusion, DALLE, Imagen, SORA, etc. have sprung up, further enriching the application prospects of generative AI. However, current diffusion models are not theoretically perfect, and few studies have paid attention to the problem of undefined singularities at the endpoints of sampling time. In addition, the average gray level caused by the singularity problem in the application and other problems that affect the quality of the generated image have not been solved.
In order to solve this problem, the WeChat vision team cooperated with Sun Yat-sen University to jointly explore the singularity problem in the diffusion model and proposed a plug-and-play method , effectively solving the sampling problem at the initial moment. This method successfully solves the average gray level problem and significantly improves the generation ability of existing diffusion models. The research results were presented at the CVPR 2024 conference.
Diffusion models have achieved remarkable success in multi-modal content generation tasks, including image, audio, text, and video generation. The successful modeling of these models mostly relies on the assumption that the inverse process of the
diffusion process also conforms to Gaussian properties. However, this hypothesis has not been fully proven. Especially at the endpoint, that is, t=0 or t=1, the singularity problem will occur, which limits the existing methods to study the sampling at the singularity.
In addition, the singularity problem will also affect the generation ability of the diffusion model, causing the model to have an
average grayscale problem, that is, it is difficult to generate strong or weak brightness image, as shown below. This also limits the application scope of current diffusion models to a certain extent.
In order to solve the singularity problem of the diffusion model at the time endpoint, the WeChat visual team cooperated with Sun Yat-sen University and conducted in-depth research from both theoretical and practical aspects. First, the team proposed an error upper bound containing an approximate Gaussian distribution of the inverse process at the singularity moment, which provided a theoretical basis for subsequent research. Based on this theoretical guarantee, the team studied sampling at singular points and came to two important conclusions: 1) The singular point at t=1 can be transformed into a detachable singular point by finding the limit, 2) The singularity at t=0 is an inherent property of the diffusion model and does not need to be avoided. Based on these conclusions, the team proposed a plug-and-play method:
SingDiffusion, to solve the problem of sampling the diffusion model at the initial moment.
A large number of experimental verifications have shown that the SingDiffusion module can be seamlessly applied to existing diffusion models with only one training, significantly solving the problem of average gray value The problem. Without using classifier-free guidance technology, SingDiffusion can significantly improve the generation quality of current methods. Especially after being applied to Stable Diffusion1.5 (SD-1.5), the quality of the generated images is improved by 33%.
Paper address: https://arxiv.org/pdf/2403.08381.pdf
Project address: https://pangzecheung.github.io/ SingDiffusion /
Thesis title: Tackling the Singularities at the Endpoints of Time Intervals in Diffusion Models
Gaussian characteristics of the inverse process
In order to study the singularity problem of the diffusion model, it is necessary to verify that the entire process including the inverse process at the singularity satisfies Gaussian properties. First define
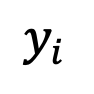 as the training sample of the diffusion model. The distribution of the training sample can be expressed as:
as the training sample of the diffusion model. The distribution of the training sample can be expressed as:
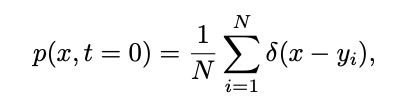
Where δ represents the Dirac function. According to the definition of continuous time diffusion model in [1], for any two moments 0≤s,t≤1, the forward process can be expressed as:
where
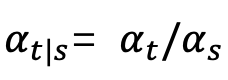 ,
,
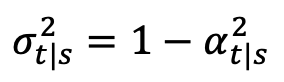 ,
,
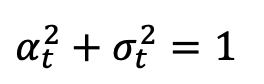 ,
,
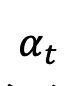 change monotonically from 1 to 0 over time. Considering the training sample distribution just defined, the single-moment marginal probability density of
change monotonically from 1 to 0 over time. Considering the training sample distribution just defined, the single-moment marginal probability density of
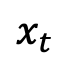 can be expressed as:
can be expressed as:
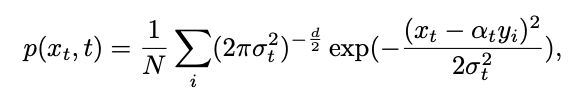
From this, the inverse process can be calculated through the Bayesian formula Conditional distribution:
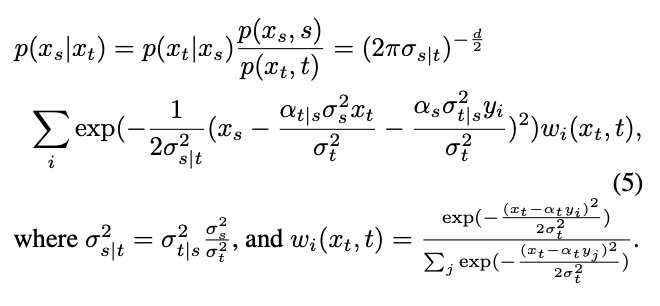
# However, the distribution passed through is a mixed Gaussian distribution, which is difficult to fit with the network. Therefore, mainstream diffusion models usually assume that this distribution can be fit by a single Gaussian distribution.
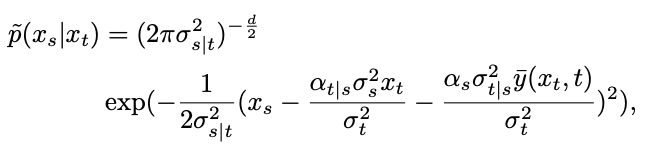
Among them,
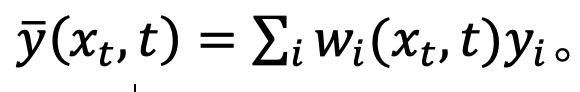 To test this hypothesis, the study estimates the error of this fit in Proposition 1.
To test this hypothesis, the study estimates the error of this fit in Proposition 1.
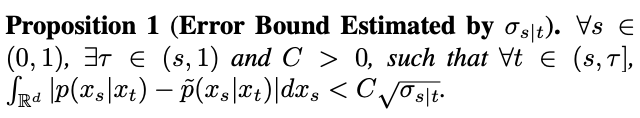
However, the study found that when t=1, as s approaches 1,
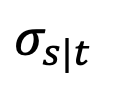 will also approach 1, and the error cannot be ignored. Therefore, Proposition 1 does not prove the inverse Gaussian property at t=1. In order to solve this problem, this study gives a new proposition:
will also approach 1, and the error cannot be ignored. Therefore, Proposition 1 does not prove the inverse Gaussian property at t=1. In order to solve this problem, this study gives a new proposition:
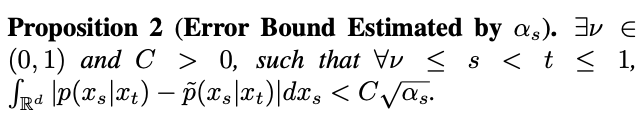
According to Proposition 2, when t=1, as s approaches 1,
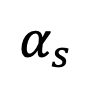 will approach 0. Thus, this study proves that the entire inverse process including the singularity moment conforms to Gaussian characteristics.
Sampling at the singularity moment
With the guarantee of Gaussian characteristics of the inverse process, This study studies the sampling of singularity moments based on the reverse sampling formula.
First consider the singularity problem at time t=1. When t=1,
will approach 0. Thus, this study proves that the entire inverse process including the singularity moment conforms to Gaussian characteristics.
Sampling at the singularity moment
With the guarantee of Gaussian characteristics of the inverse process, This study studies the sampling of singularity moments based on the reverse sampling formula.
First consider the singularity problem at time t=1. When t=1,
 =0, the following sampling formula will have the denominator divided by 0:
=0, the following sampling formula will have the denominator divided by 0:
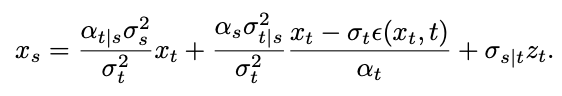
The research team found that by calculating the limit, the singular point This can be converted into a desingularity point:
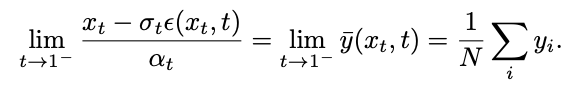
However, this limit cannot be calculated during testing. To this end, this study proposes to fit
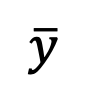 at time t=1 and use "x - prediction" to solve the sampling problem at the initial singular point.
Then consider the time t=0, the inverse process of Gaussian distribution fitting will become a Gaussian distribution with a variance of 0, that is, the Dirac function:
at time t=1 and use "x - prediction" to solve the sampling problem at the initial singular point.
Then consider the time t=0, the inverse process of Gaussian distribution fitting will become a Gaussian distribution with a variance of 0, that is, the Dirac function:
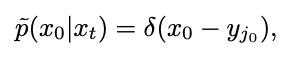
in
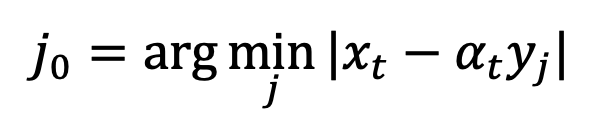 . Such singularities will cause the sampling process to converge to the correct data
. Such singularities will cause the sampling process to converge to the correct data
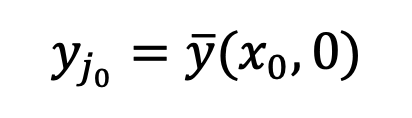 . Therefore, the singularity at t=0 is a good property of the diffusion model and does not need to be avoided.
In addition, the study also explores the singularity problem in DDIM, SDE, and ODE in the appendix.
Plug and play SingDiffusion module
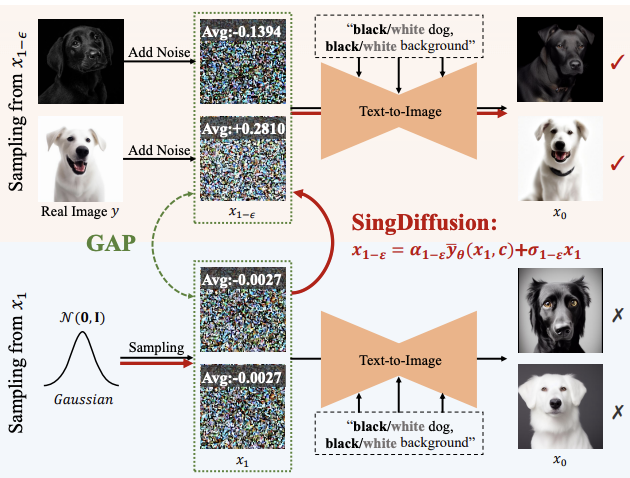
Sampling at singular points will affect The quality of images generated by diffusion models. For example, when inputting cues of high or low brightness, existing methods often can only generate images with average grayscale, which is called the average grayscale problem. This problem stems from the fact that the existing method ignores the sampling at the singular point when t=0, but uses the
standard Gaussian distributionas the initial distribution for sampling at the 1-ϵ moment. However, as shown in the figure above, there is a large gap between the standard Gaussian distribution and the actual data distribution at 1-ϵ time.
. Therefore, the singularity at t=0 is a good property of the diffusion model and does not need to be avoided.
In addition, the study also explores the singularity problem in DDIM, SDE, and ODE in the appendix.
Plug and play SingDiffusion module
Sampling at singular points will affect The quality of images generated by diffusion models. For example, when inputting cues of high or low brightness, existing methods often can only generate images with average grayscale, which is called the average grayscale problem. This problem stems from the fact that the existing method ignores the sampling at the singular point when t=0, but uses the
standard Gaussian distributionas the initial distribution for sampling at the 1-ϵ moment. However, as shown in the figure above, there is a large gap between the standard Gaussian distribution and the actual data distribution at 1-ϵ time.
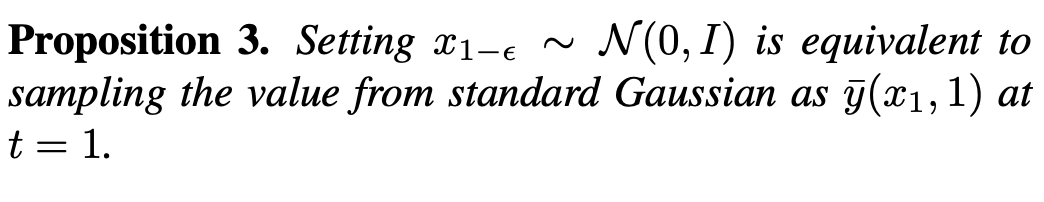
Under such a gap, according to Proposition 3, the existing method is equivalent to generating an image with a mean value of 0 at t=1, that is, an average grayscale image. Therefore, it is difficult for existing methods to generate images with extremely strong or weak brightness. To solve this problem, this study proposes a plug-and-play SingDiffusion method to bridge this gap by fitting the conversion between a standard Gaussian distribution and the actual data distribution.
The algorithm of SingDiffuion is shown in the figure below:

According to the conclusion of the previous section, this research is in t =1 moment uses the "x - prediction" method to solve the sampling problem at the singular point. For image-text data pair
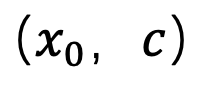 , this method trains a Unet
, this method trains a Unet
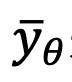 to fit
to fit
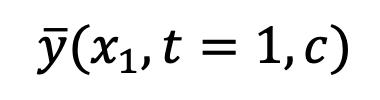 . The loss function is expressed as:
. The loss function is expressed as:
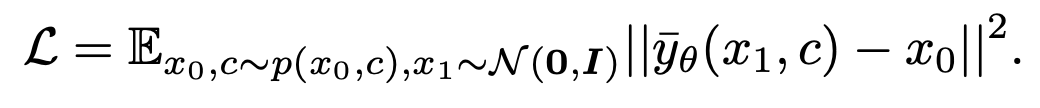
After the model has converged, you can follow the DDIM sampling formula below and use the newly obtained module
 sampling
sampling
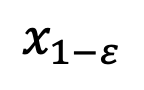 .
.
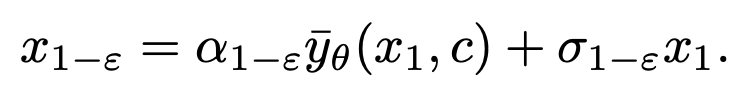
The sampling formula of DDIM ensures that the generated
 conforms to the data distribution
conforms to the data distribution
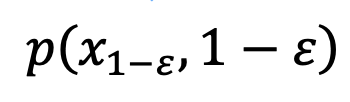 at the 1-ε moment, thereby solving the average grayscale problem. After this step, the pretrained model can be used to perform subsequent sampling steps until
at the 1-ε moment, thereby solving the average grayscale problem. After this step, the pretrained model can be used to perform subsequent sampling steps until
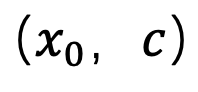 is generated. It is worth noting that since this method only participates in the first step of sampling and has nothing to do with the subsequent sampling process, SingDiffusion can be applied to most existing diffusion models. In addition, in order to avoid data overflow problems caused by no classifier guidance operation, this method also uses the following normalization operation:
is generated. It is worth noting that since this method only participates in the first step of sampling and has nothing to do with the subsequent sampling process, SingDiffusion can be applied to most existing diffusion models. In addition, in order to avoid data overflow problems caused by no classifier guidance operation, this method also uses the following normalization operation:
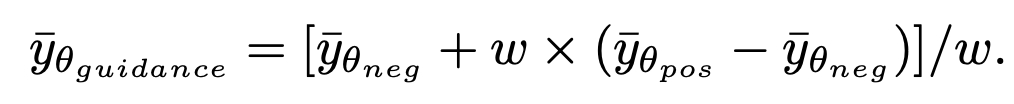
where guidance represents no classifier guidance operation In the final result, neg represents the output under negative cues, pos represents the output under positive cues, and ω represents the strength of guidance.
First of all, the study was conducted in SD-1.5, SD-2.0- The ability of SingDiffusion to solve the average grayscale problem was verified on three models: base and SD-2.0. This study selected four extreme prompts, including "pure white/black background" and "monochrome line art logo on white/black background", as conditions for generation, and calculated the average grayscale value of the generated image, as shown in the table below Shown:
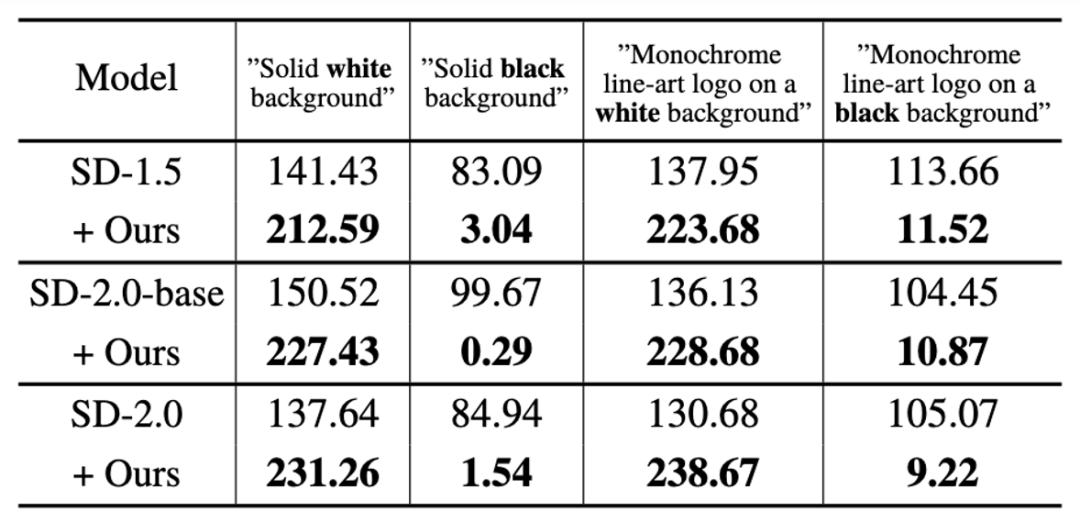
#As can be seen from the table, this research can significantly solve the problem of average gray value and generate images that match the brightness of the input text description. In addition, the study also visualized the generation results under these four prompt statements, as shown in the following figure:

As can be seen from the figure, after adding this method, Existing diffusion models can generate black or white images.
To further study the improvement of image quality achieved by this method, the study selected 30,000 descriptions for testing on the COCO dataset. First of all, this study demonstrates the generative ability of the model itself without using classifier guidance, as shown in the following table:

As can be seen from the table, the proposed The method can significantly reduce the FID of the generated image and improve the CLIP index. It is worth noting that in the SD-1.5 model, the method in this paper reduces the FID index by 33% compared to the original model.
Further, in order to verify the generation ability of the proposed method without classifier guidance, the study also shows in the figure below that under different guidance sizes ω∈[1.5, 2,3,4,5,6,7,8] Pareto curve of CLIP vs. FID:
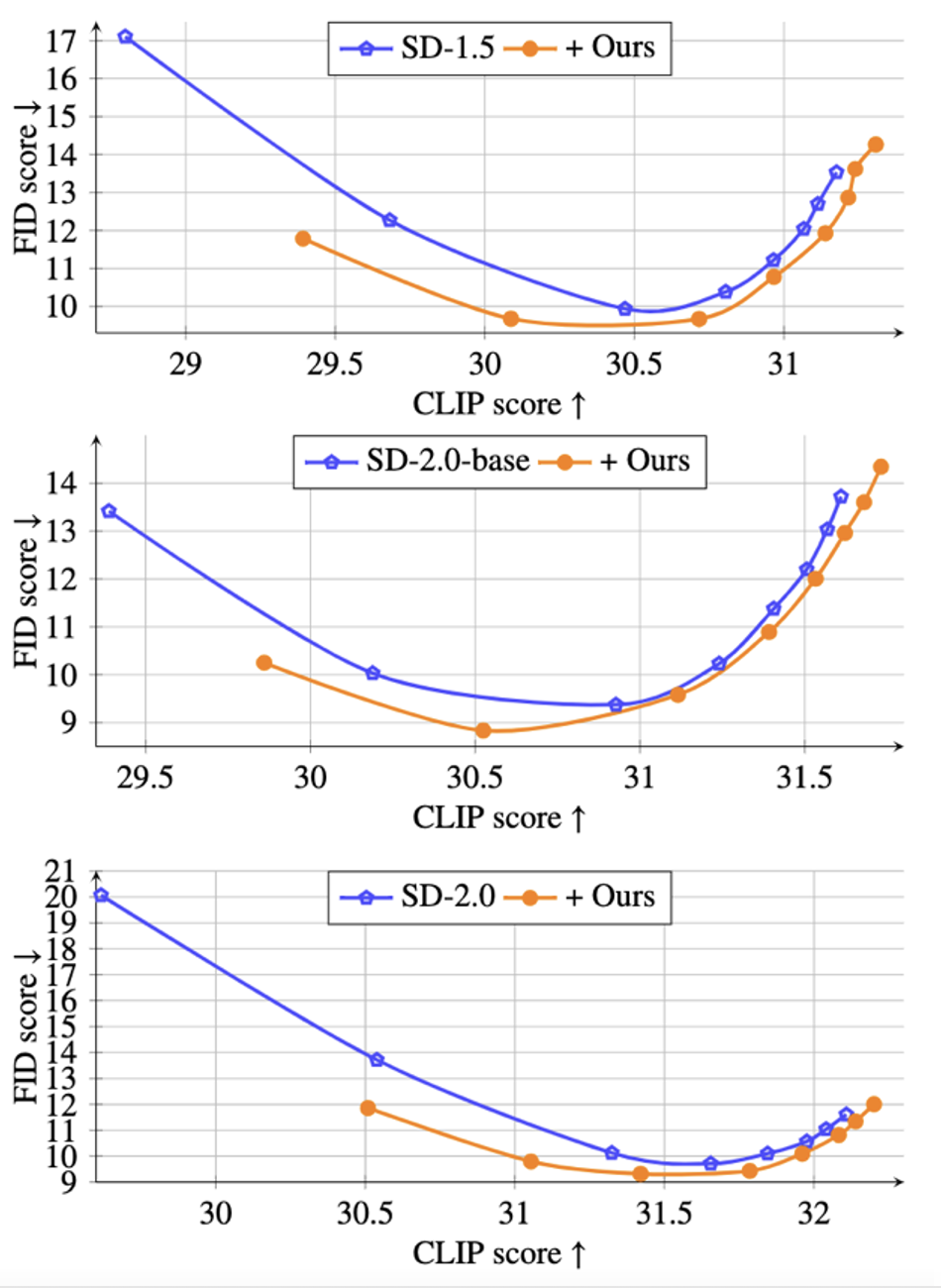
It can be seen from the figure that at the same CLIP level, the proposed method can obtain lower FID values and generate more realistic images.
In addition, this study also demonstrates the generalization ability of the proposed method under different CIVITAI pre-training models, as shown in the following figure:

It can be seen that the method proposed in this study only needs one training and can be easily applied to existing diffusion models to solve the average grayscale problem.
Finally, the method proposed in this study can also be seamlessly applied to the pre-trained ControlNet model, as shown in the figure below:

From the results It can be seen that this method can effectively solve the average grayscale problem of ControlNet.
[1] Tero Karras, Miika Aittala, Timo Aila, and Samuli Laine. Elucidating the design space of diffusion-based generative models. Advances in Neural Information Processing Systems (NeurIPS), pages 26565–26577, 2022. 3
The above is the detailed content of CVPR 2024|Can't generate images with extremely strong light? WeChat Vision Team effectively solves the singularity problem of diffusion model. For more information, please follow other related articles on the PHP Chinese website!


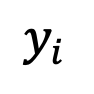 as the training sample of the diffusion model. The distribution of the training sample can be expressed as:
as the training sample of the diffusion model. The distribution of the training sample can be expressed as:
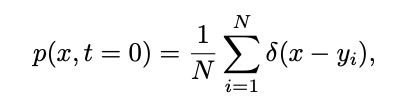
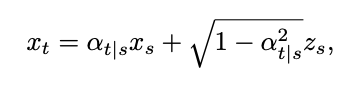
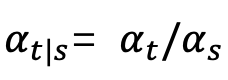 ,
,
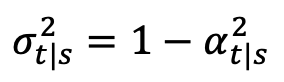 ,
,
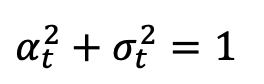 ,
,
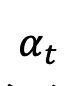 change monotonically from 1 to 0 over time. Considering the training sample distribution just defined, the single-moment marginal probability density of
change monotonically from 1 to 0 over time. Considering the training sample distribution just defined, the single-moment marginal probability density of
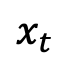 can be expressed as:
can be expressed as:
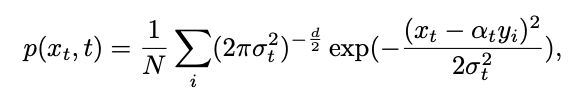
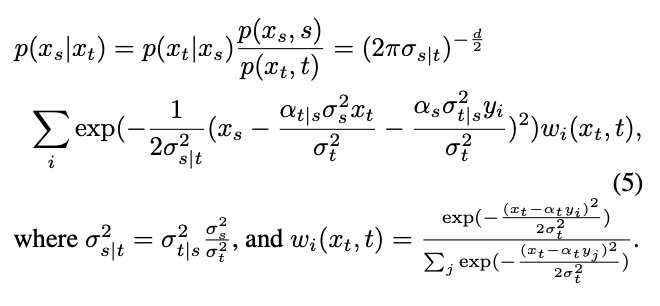
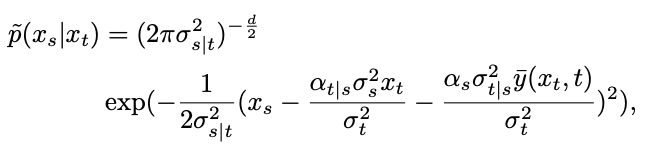
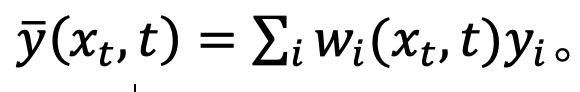 To test this hypothesis, the study estimates the error of this fit in Proposition 1.
To test this hypothesis, the study estimates the error of this fit in Proposition 1.
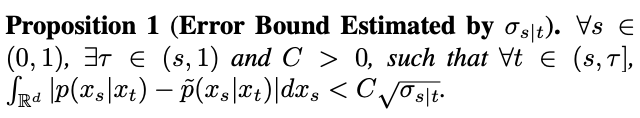
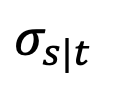 will also approach 1, and the error cannot be ignored. Therefore, Proposition 1 does not prove the inverse Gaussian property at t=1. In order to solve this problem, this study gives a new proposition:
will also approach 1, and the error cannot be ignored. Therefore, Proposition 1 does not prove the inverse Gaussian property at t=1. In order to solve this problem, this study gives a new proposition:
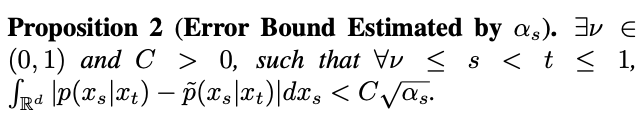
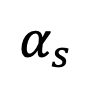 will approach 0. Thus, this study proves that the entire inverse process including the singularity moment conforms to Gaussian characteristics.
will approach 0. Thus, this study proves that the entire inverse process including the singularity moment conforms to Gaussian characteristics.
 =0, the following sampling formula will have the denominator divided by 0:
=0, the following sampling formula will have the denominator divided by 0:
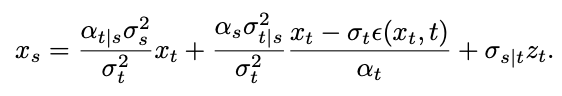
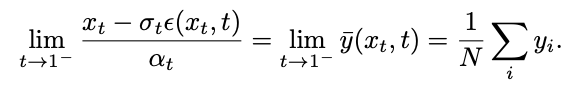
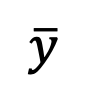 at time t=1 and use "x - prediction" to solve the sampling problem at the initial singular point.
at time t=1 and use "x - prediction" to solve the sampling problem at the initial singular point.
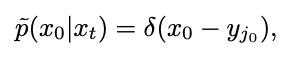
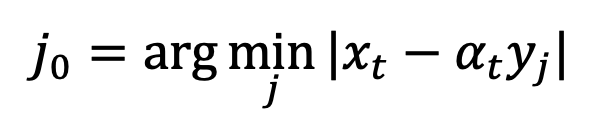 . Such singularities will cause the sampling process to converge to the correct data
. Such singularities will cause the sampling process to converge to the correct data
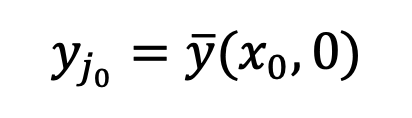 . Therefore, the singularity at t=0 is a good property of the diffusion model and does not need to be avoided.
. Therefore, the singularity at t=0 is a good property of the diffusion model and does not need to be avoided.
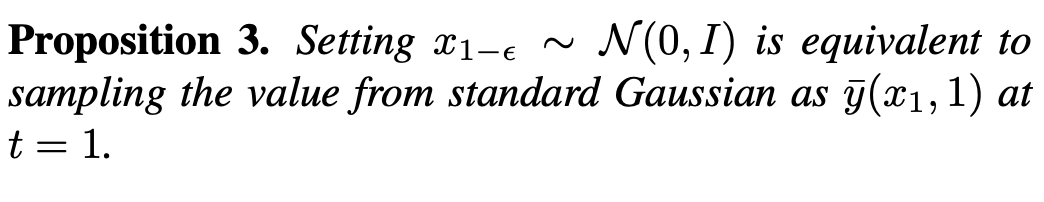

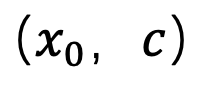 , this method trains a Unet
, this method trains a Unet
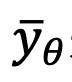 to fit
to fit
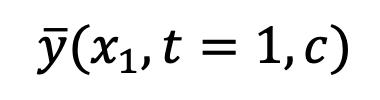 . The loss function is expressed as:
. The loss function is expressed as:
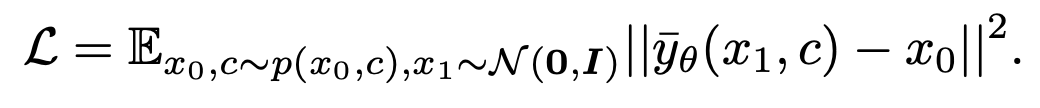
 sampling
sampling
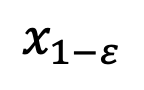 .
.
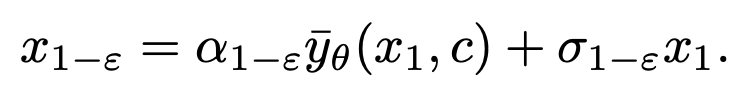
 conforms to the data distribution
conforms to the data distribution
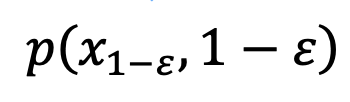 at the 1-ε moment, thereby solving the average grayscale problem. After this step, the pretrained model can be used to perform subsequent sampling steps until
at the 1-ε moment, thereby solving the average grayscale problem. After this step, the pretrained model can be used to perform subsequent sampling steps until
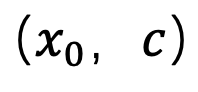 is generated. It is worth noting that since this method only participates in the first step of sampling and has nothing to do with the subsequent sampling process, SingDiffusion can be applied to most existing diffusion models. In addition, in order to avoid data overflow problems caused by no classifier guidance operation, this method also uses the following normalization operation:
is generated. It is worth noting that since this method only participates in the first step of sampling and has nothing to do with the subsequent sampling process, SingDiffusion can be applied to most existing diffusion models. In addition, in order to avoid data overflow problems caused by no classifier guidance operation, this method also uses the following normalization operation:
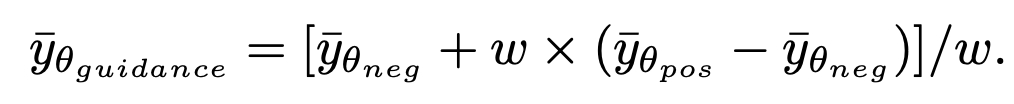






 How to buy and sell Bitcoin on Huobi.com
How to buy and sell Bitcoin on Huobi.com Win11 My Computer Added to Desktop Tutorial
Win11 My Computer Added to Desktop Tutorial Tutorial on turning off Windows 11 Security Center
Tutorial on turning off Windows 11 Security Center How to remove the watermark of Douyin account from downloaded videos from Douyin
How to remove the watermark of Douyin account from downloaded videos from Douyin What is the difference between 5g and 4g
What is the difference between 5g and 4g How to watch live broadcast playback records on Douyin
How to watch live broadcast playback records on Douyin What are the dos commands?
What are the dos commands? The difference between vscode and visual studio
The difference between vscode and visual studio



