The principles and characteristics of red-black trees and their code implementation in Python-Python Tutorial-php.cn

The red-black tree, like the B-tree, is a balanced binary search tree. Each node of a red-black tree is colored, either red or black, but the roots of the tree are black and the leaves at the bottom are also black. Also note that the direct path from any node to a leaf in a red-black tree contains the same number of black nodes.

How do red-black trees maintain self-balancing characteristics?

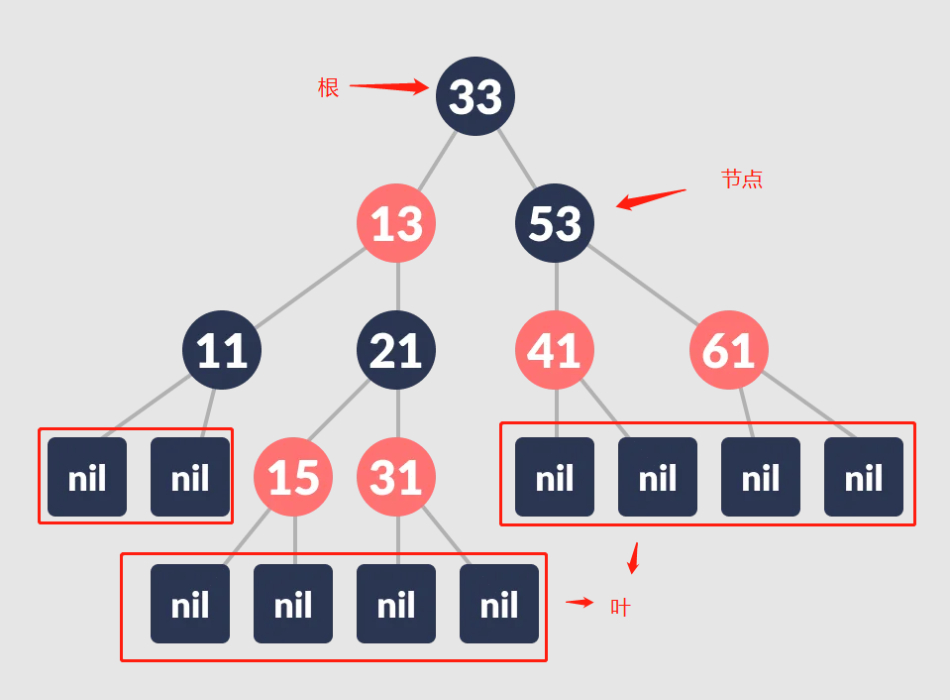
The restriction on red-black tree node colors ensures that the longest path from root to leaf does not exceed twice the shortest path.

Why are newly inserted nodes always red in red-black trees?

This is because inserting a red node does not violate the black node quantity property of the red-black tree. And even if a new red node is inserted into the original red node, solving this problem will be easier than the problem caused by violating the black node.

Red-black tree Python code implementation

import sys # 创建节点 class Node(): def __init__(self, item): self.item = item self.parent = None self.left = None self.right = None self.color = 1 class RedBlackTree(): def __init__(self): self.TNULL = Node(0) self.TNULL.color = 0 self.TNULL.left = None self.TNULL.right = None self.root = self.TNULL # 前序 def pre_order_helper(self, node): if node != TNULL: sys.stdout.write(node.item + " ") self.pre_order_helper(node.left) self.pre_order_helper(node.right) # 中序 def in_order_helper(self, node): if node != TNULL: self.in_order_helper(node.left) sys.stdout.write(node.item + " ") self.in_order_helper(node.right) # 后根 def post_order_helper(self, node): if node != TNULL: self.post_order_helper(node.left) self.post_order_helper(node.right) sys.stdout.write(node.item + " ") # 搜索树 def search_tree_helper(self, node, key): if node == TNULL or key == node.item: return node if key < node.item: return self.search_tree_helper(node.left, key) return self.search_tree_helper(node.right, key) # 删除后平衡树 def delete_fix(self, x): while x != self.root and x.color == 0: if x == x.parent.left: s = x.parent.right if s.color == 1: s.color = 0 x.parent.color = 1 self.left_rotate(x.parent) s = x.parent.right if s.left.color == 0 and s.right.color == 0: s.color = 1 x = x.parent else: if s.right.color == 0: s.left.color = 0 s.color = 1 self.right_rotate(s) s = x.parent.right s.color = x.parent.color x.parent.color = 0 s.right.color = 0 self.left_rotate(x.parent) x = self.root else: s = x.parent.left if s.color == 1: s.color = 0 x.parent.color = 1 self.right_rotate(x.parent) s = x.parent.left if s.right.color == 0 and s.right.color == 0: s.color = 1 x = x.parent else: if s.left.color == 0: s.right.color = 0 s.color = 1 self.left_rotate(s) s = x.parent.left s.color = x.parent.color x.parent.color = 0 s.left.color = 0 self.right_rotate(x.parent) x = self.root x.color = 0 def __rb_transplant(self, u, v): if u.parent == None: self.root = v elif u == u.parent.left: u.parent.left = v else: u.parent.right = v v.parent = u.parent # 节点删除 def delete_node_helper(self, node, key): z = self.TNULL while node != self.TNULL: if node.item == key: z = node if node.item <= key: node = node.right else: node = node.left if z == self.TNULL: print("Cannot find key in the tree") return y = z y_original_color = y.color if z.left == self.TNULL: x = z.right self.__rb_transplant(z, z.right) elif (z.right == self.TNULL): x = z.left self.__rb_transplant(z, z.left) else: y = self.minimum(z.right) y_original_color = y.color x = y.right if y.parent == z: x.parent = y else: self.__rb_transplant(y, y.right) y.right = z.right y.right.parent = y self.__rb_transplant(z, y) y.left = z.left y.left.parent = y y.color = z.color if y_original_color == 0: self.delete_fix(x) # 插入后平衡树 def fix_insert(self, k): while k.parent.color == 1: if k.parent == k.parent.parent.right: u = k.parent.parent.left if u.color == 1: u.color = 0 k.parent.color = 0 k.parent.parent.color = 1 k = k.parent.parent else: if k == k.parent.left: k = k.parent self.right_rotate(k) k.parent.color = 0 k.parent.parent.color = 1 self.left_rotate(k.parent.parent) else: u = k.parent.parent.right if u.color == 1: u.color = 0 k.parent.color = 0 k.parent.parent.color = 1 k = k.parent.parent else: if k == k.parent.right: k = k.parent self.left_rotate(k) k.parent.color = 0 k.parent.parent.color = 1 self.right_rotate(k.parent.parent) if k == self.root: break self.root.color = 0 # Printing the tree def __print_helper(self, node, indent, last): if node != self.TNULL: sys.stdout.write(indent) if last: sys.stdout.write("R----") indent += " " else: sys.stdout.write("L----") indent += "| " s_color = "RED" if node.color == 1 else "BLACK" print(str(node.item) + "(" + s_color + ")") self.__print_helper(node.left, indent, False) self.__print_helper(node.right, indent, True) def preorder(self): self.pre_order_helper(self.root) def inorder(self): self.in_order_helper(self.root) def postorder(self): self.post_order_helper(self.root) def searchTree(self, k): return self.search_tree_helper(self.root, k) def minimum(self, node): while node.left != self.TNULL: node = node.left return node def maximum(self, node): while node.right != self.TNULL: node = node.right return node def successor(self, x): if x.right != self.TNULL: return self.minimum(x.right) y = x.parent while y != self.TNULL and x == y.right: x = y y = y.parent return y def predecessor(self, x): if (x.left != self.TNULL): return self.maximum(x.left) y = x.parent while y != self.TNULL and x == y.left: x = y y = y.parent return y def left_rotate(self, x): y = x.right x.right = y.left if y.left != self.TNULL: y.left.parent = x y.parent = x.parent if x.parent == None: self.root = y elif x == x.parent.left: x.parent.left = y else: x.parent.right = y y.left = x x.parent = y def right_rotate(self, x): y = x.left x.left = y.right if y.right != self.TNULL: y.right.parent = x y.parent = x.parent if x.parent == None: self.root = y elif x == x.parent.right: x.parent.right = y else: x.parent.left = y y.right = x x.parent = y def insert(self, key): node = Node(key) node.parent = None node.item = key node.left = self.TNULL node.right = self.TNULL node.color = 1 y = None x = self.root while x != self.TNULL: y = x if node.item < x.item: x = x.left else: x = x.right node.parent = y if y == None: self.root = node elif node.item < y.item: y.left = node else: y.right = node if node.parent == None: node.color = 0 return if node.parent.parent == None: return self.fix_insert(node) def get_root(self): return self.root def delete_node(self, item): self.delete_node_helper(self.root, item) def print_tree(self): self.__print_helper(self.root, "", True) if __name__ == "__main__": bst = RedBlackTree() bst.insert(55) bst.insert(40) bst.insert(65) bst.insert(60) bst.insert(75) bst.insert(57) bst.print_tree() print("\nAfter deleting an element") bst.delete_node(40) bst.print_tree()

Copy after login

The above is the detailed content of The principles and characteristics of red-black trees and their code implementation in Python. For more information, please follow other related articles on the PHP Chinese website!