
In this article, we will introduce a popular machine learning project - text generator. You will learn how to build a text generator and learn how to implement a Markov chain to achieve a faster prediction model.
Text generation is popular across industries, especially in mobile, apps, and data science. Even the press uses text generation to aid the writing process.
In daily life, we will come into contact with some text generation technologies. Text completion, search suggestions, Smart Compose, and chat robots are all examples of applications.
This article will use Markov chain to build A text generator. This would be a character-based model that takes the previous character of the chain and generates the next letter in the sequence.
By training our program using example words, the text generator will learn common character order patterns. The text generator will then apply these patterns to the input, which is an incomplete word, and output the character with the highest probability of completing the word.
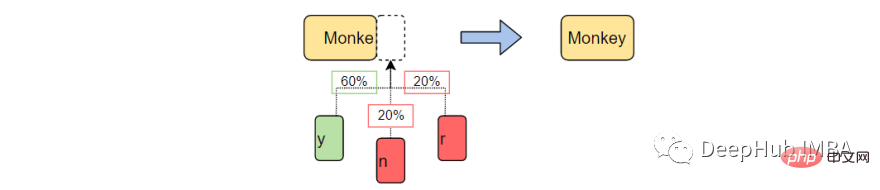
#Text generation is a branch of natural language processing that predicts and generates the next character based on previously observed language patterns.
Before machine learning, NLP performed text generation by creating a table containing all the words in the English language and matching the passed string to the existing words. There are two problems with this approach.
The advent of machine learning and deep learning has allowed us to drastically reduce runtime and increase generality in NLP because the generator can complete words it has never encountered before. NLP can be extended to predict words, phrases or sentences if desired!
For this project we will be doing it exclusively using Markov chains. Markov processes are the basis of many natural language processing projects involving written language and simulating samples from complex distributions.
Markov processes are so powerful that they can be used to generate ostensibly real-looking text using only a sample document.
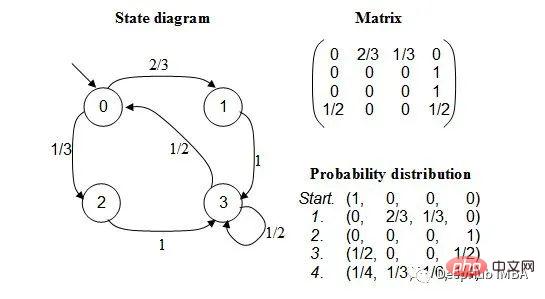
A Markov chain is a stochastic process that models a sequence of events where the probability of each event depends on the state of the previous event . The model has a finite set of states, and the conditional probability of moving from one state to another is fixed.
The probability of each transition only depends on the previous state of the model, not the entire history of events.
For example, suppose you want to build a Markov chain model to predict weather.
In this model we have two states, sunny or rainy. If we have a sunny day today, there is a higher probability (70%) that it will be sunny tomorrow. The same goes for rain; if it's already rained, it's likely to continue to rain.
But it is possible (30%) that the weather will change state, so we include that in our Markov chain model as well.
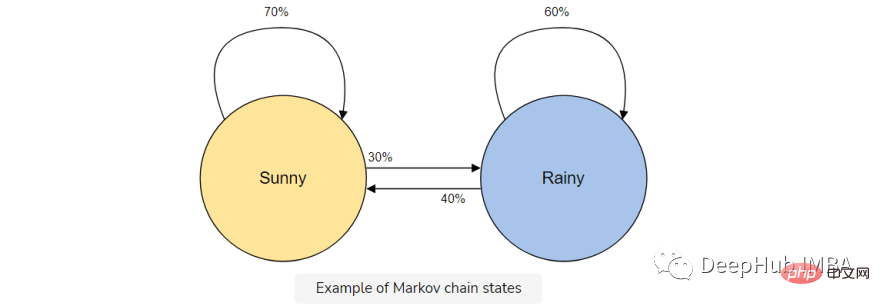
Markov chains are the perfect model for our text generator because our model will predict the next character using only the previous character. The advantages of using a Markov chain are that it is accurate, requires less memory (only 1 previous state is stored) and is fast to execute.
The text generator will be completed in 6 steps:

First, we will create a table to record the occurrence of each character state in the training corpus. Save the last 'K' character and 'K1' character from the training corpus and save them in a lookup table.
For example, imagine that our training corpus contains, "the man was, they, then, the, the". Then the number of occurrences of the word is:
The following are the results in the lookup table:

In the above example, we take K = 3, which means that 3 characters will be considered at a time and the next character (K 1) will be used as the output character. Treat the word (X) as a character in the above lookup table and the output character (Y) as a single space (" ") since there is no word after the first the. Also calculated is the number of times this sequence appears in the data set, in this case 3 times.
This generates data for each word in the corpus, that is, all possible X and Y pairs are generated.
Here's how we generate the lookup table in the code:
def generateTable(data,k=4):
T = {}
for i in range(len(data)-k):
X = data[i:i+k]
Y = data[i+k]
#print("X %s and Y %s "%(X,Y))
if T.get(X) is None:
T[X] = {}
T[X][Y] = 1
else:
if T[X].get(Y) is None:
T[X][Y] = 1
else:
T[X][Y] += 1
return T
T = generateTable("hello hello helli")
print(T)
#{'llo ': {'h': 2}, 'ello': {' ': 2}, 'o he': {'l': 2}, 'lo h': {'e': 2}, 'hell': {'i': 1, 'o': 2}, ' hel': {'l': 2}}Simple explanation of the code:
In line 3, a dictionary is created that will store X and Its corresponding Y and frequency values. Lines 9 to 17 check for occurrences of X and Y. If there is already an X and Y pair in the lookup dictionary, just increase it by 1.
Once we have this table and the number of occurrences, we can get the probability of Y occurring after a given occurrence of x. The formula is:
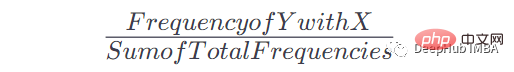
For example, if X = the, Y = n, our formula is like this:
When X =the Y = n Frequency: 2, total frequency in the table: 8, therefore: P = 2/8= 0.125= 12.5%
Here is how we apply this formula to convert the lookup table into a Markov chain with usable probabilities:
def convertFreqIntoProb(T):
for kx in T.keys():
s = float(sum(T[kx].values()))
for k in T[kx].keys():
T[kx][k] = T[kx][k]/s
return T
T = convertFreqIntoProb(T)
print(T)
#{'llo ': {'h': 1.0}, 'ello': {' ': 1.0}, 'o he': {'l': 1.0}, 'lo h': {'e': 1.0}, 'hell': {'i': 0.3333333333333333, 'o': 0.6666666666666666}, ' hel': {'l': 1.0}}Simple explanation:
Add the frequency values of a specific key, and then divide each frequency value of this key by the added value to get the probability.
The real training corpus will be loaded next. You can use any long text (.txt) document you want.
For simplicity a political speech will be used to provide enough vocabulary to teach our model.
text_path = "train_corpus.txt"
def load_text(filename):
with open(filename,encoding='utf8') as f:
return f.read().lower()
text = load_text(text_path)
print('Loaded the dataset.')This data set can provide enough events for our sample project to make reasonably accurate predictions. As with all machine learning, a larger training corpus will produce more accurate predictions.
Let us build a Markov chain and associate the probability with each character. The generateTable() and convertFreqIntoProb() functions created in steps 1 and 2 will be used here to build the Markov model.
def MarkovChain(text,k=4): T = generateTable(text,k) T = convertFreqIntoProb(T) return T model = MarkovChain(text)
In line 1, a method is created to generate a Markov model. The method accepts a text corpus and a K value, which is the value that tells the Markov model to consider K characters and predict the next character. Line 2, the lookup table is generated by providing the text corpus and K to the method generateTable(), which we created in the previous section. Line 3 converts the frequency to a probability value using the convertFreqIntoProb() method, which we also created in the previous lesson.
Create a sampling function that uses the unfinished words (ctx), the Markov chain model (model) in step 4 and the base for forming the word The number of characters (k).
We will use this function to sample the passed context and return the next possible character and determine the probability that it is the correct character.
import numpy as np
def sample_next(ctx,model,k):
ctx = ctx[-k:]
if model.get(ctx) is None:
return " "
possible_Chars = list(model[ctx].keys())
possible_values = list(model[ctx].values())
print(possible_Chars)
print(possible_values)
return np.random.choice(possible_Chars,p=possible_values)
sample_next("commo",model,4)
#['n']
#[1.0]Code explanation:
The function sample_next accepts three parameters: ctx, model and k value.
ctx is the text used to generate some new text. But here only the last K characters in ctx will be used by the model to predict the next character in the sequence. For example, we pass common, K = 4, and the text that the model uses to generate the next character is ommo, because the Markov model only uses the previous history.
On lines 9 and 10, the possible characters and their probability values are printed, since these characters also exist in our model. We get the next predicted character to be n, with probability 1.0. Since the word commo is more likely to be more common after generating the next character
on line 12, we return a character based on the probability value discussed above.
Finally combine all the above functions to generate some text.
def generateText(starting_sent,k=4,maxLen=1000):
sentence = starting_sent
ctx = starting_sent[-k:]
for ix in range(maxLen):
next_prediction = sample_next(ctx,model,k)
sentence += next_prediction
ctx = sentence[-k:]
return sentence
print("Function Created Successfully!")
text = generateText("dear",k=4,maxLen=2000)
print(text)The results are as follows:
dear country brought new consciousness. i heartily great service of their lives, our country, many of tricoloring a color flag on their lives independence today.my devoted to be oppression of independence.these day the obc common many country, millions of oppression of massacrifice of indian whom everest. my dear country is not in the sevents went was demanding and nights by plowing in the message of the country is crossed, oppressed, women, to overcrowding for years of the south, it is like the ashok chakra of constitutional states crossed, deprived, oppressions of freedom, i bow my heart to proud of our country.my dear country, millions under to be a hundred years of the south, it is going their heroes.
The above function accepts three parameters: the starting word of the generated text, the value of K and the maximum character length of the required text. Running the code will result in a 2000 character text starting with "dear".
While this speech may not make much sense, the words are complete and often imitate familiar patterns in words.
This is a simple text generation project. Use this project to learn how natural language processing and Markov chains work in action, which you can use as you continue your deep learning journey.
This article is just to introduce the experimental project carried out by Markov chain, because it will not play any role in actual application. If you want to get better text generation effect, then please learn GPT- 3 such tools.
The above is the detailed content of Building text generators using Markov chains. For more information, please follow other related articles on the PHP Chinese website!




